رسم خرائط سطحية للكواكب الخارجية الشبيهة بالأرض باستخدام منحنيات الضوء نقطة واحدة

Summary

يستخرج البروتوكول المعلومات من منحنيات الضوء للكواكب الخارجية وينشئ خرائط سطحها. ويستخدم منحنيات خفيفة من الأرض، والتي هي بمثابة كوكب خارجي بالوكالة، لإثبات النهج.

Abstract

إن حل خصائص الكواكب الخارجية من نقطة واحدة أمر ضروري لتقييم إمكانية قابلية الكواكب الخارجية للسكن. والهدف النهائي لهذا البروتوكول هو تحديد ما إذا كانت هذه العوالم الكوكبية تضم سمات جيولوجية و/أو أنظمة مناخية. نقدم طريقة لاستخراج المعلومات من منحنيات الضوء أحادية الطول الموجي المتعددة واسترجاع الخرائط السطحية. ويستخدم التحلل من حيث القيمة المفردة (SVD) لفصل المصادر التي تسهم في تغير المنحنى الضوئي والاستدلال على وجود أنظمة مناخية غائمة جزئياً. ومن خلال تحليل السلاسل الزمنية التي تم الحصول عليها من نظام SVD، يمكن الاستدلال على المكونات المادية للمكونات الرئيسية دون افتراضات بشأن أي خصائص طيفية. وبالجمع بين هندسة المشاهدة، من الممكن إعادة بناء الخرائط السطحية إذا وجد أن أحد أجهزة الكمبيوتر يحتوي على معلومات سطحية. إنّ الهدّان نشأت من التواء هندسة البكسل ومعلومات الطيف الذي يحدد جودة الخرائط السطحية المعاد بناؤها، الأمر الذي يتطلب إدخال الانتظام. لغرض إظهار البروتوكول ، يتم تحليل منحنيات الضوء متعدد الأطوال الموجية للأرض ، والتي تعمل بمثابة كوكب خارجي بالوكالة. يتم عرض المقارنة بين النتائج والحقيقة الأساسية لإظهار أداء البروتوكول وحدوده. ويوفر هذا العمل معياراً للتعميم المستقبلي لتطبيقات الكواكب الخارجية.

Introduction

تحديد عوالم صالحة للسكن هو واحد من الأهداف النهائية في علم الأحياء الفلكية¹. منذ الكشف الأول²، أكثر من 4000 الكواكب الخارجية وقد تم تأكيد حتى الآن³ مع عدد من النظير الأرض (على سبيل المثال ، TRAPPIST - 1e)^4. هذه الكواكب لها خصائص مدارية وكوكبية مماثلة لتلك الموجودة في الأرض، وبالتالي يمكن أن تكون صالحة للسكن. ومن الضروري في هذا السياق تقييم صلاحيتها للسكن من خلال ملاحظات محدودة. واستنادا إلى معرفة الحياة على الأرض، تعتبر النظم الجيولوجية والمناخية حاسمة الأهمية بالنسبة للصلاحية للسكن، التي يمكن أن تكون بالتالي بمثابة توقيعات بيولوجية. ومن حيث المبدأ، يمكن ملاحظة ملامح هذه النظم من مسافة بعيدة حتى عندما لا يمكن حل كوكب ما مكانياً أفضل من نقطة واحدة. وفي هذه الحالة، فإن تحديد المعالم الجيولوجية والنظم المناخية من منحنيات الضوء ذات النقطة الواحدة أمر ضروري عند تقييم صلاحية الكواكب الخارجية للسكن. يصبح رسم الخرائط السطحية لهذه الكواكب الخارجية أمراً ملحاً.

على الرغم من الالتواء بين هندسة المشاهدة والخصائص الطيفية، يتم تضمين معلومات سطح الكوكب الخارجي في منحنيات الضوء ذات النقطة الواحدة التي تم حلها زمنيًا، والتي يمكن الحصول عليها من مسافة بعيدة، والتي يتم الحصول عليها بملاحظات كافية. ومع ذلك، فإن رسم الخرائط السطحية ثنائية الأبعاد للكواكب الخارجية التي يمكن أن تكون صالحة للسكن على الأرض يشكل تحدياً بسبب تأثير السحب. وقد تم تطوير واختبار أساليب استرجاع الخرائط 2D باستخدام منحنيات الإضاءة محاكاة والأطياف المعروفة^5،6،7،8، لكنها لم تطبق على الملاحظات الحقيقية. وعلاوة على ذلك، قد تكون افتراضات الأطياف المميزة مثيرة للجدل في تحليلات عمليات رصد الكواكب الخارجية في الوقت الحاضر وفي المستقبل القريب عندما لا تكون التراكيب السطحية الكوكبية مقيدة بشكل جيد.

في هذه الورقة، نُظهر تقنية رسم خرائط سطحية للكواكب الخارجية الشبيهة بالأرض. نحن نستخدم SVD لتقييم وفصل المعلومات من مصادر مختلفة التي ترد في منحنيات ضوء متعدد الطول الموجي دون افتراضات من أي أطياف محددة. جنبا إلى جنب مع هندسة العرض، ونحن نقدم إعادة بناء الخرائط السطحية باستخدام معلومات سطحية حل في الوقت المناسب ولكن معقدة مكانيا. ولغرض إثبات هذه الطريقة، يجري تحليل عمليات رصد الأرض ذات الطول الموجي المتعدد الطول لمدة سنتين من نقطة واحدة يحصل عليها مرصد المناخ السحيق/كاميرا التصوير متعدد الألوان للأرض (DSCOVR/EPIC؛ www.nesdis.noaa.gov/DSCOVR/spacecraft.html). نحن نستخدم الأرض ككوكب خارجي بالوكالة لتقييم هذه الطريقة لأن عمليات الرصد المتاحة حاليًا للكواكب الخارجية ليست كافية. نرفق الرمز مع ورقة كمثال. وقد تم تطويره تحت الثعبان 3.7 مع حزم أناكوندا و healpy ، ولكن يمكن أيضا أن يتم الرياضيات من البروتوكول في بيئات البرمجة الأخرى (على سبيل المثال ، IDL أو MATLAB).

Protocol

1. إعداد البرمجة

1. إعداد بيئة البرمجة للتعليمات البرمجية المرفقة. مطلوب جهاز كمبيوتر مع نظام التشغيل لينكس، كما لا تتوفر حزمة healpy على ويندوز. التعليمات البرمجية غير مكلفة حسابياً، لذا يمكن للكمبيوتر الشخصي العادي معالجة البروتوكول.
2. اتبع التعليمات (https://docs.anaconda.com/anaconda/install/linux/) لتثبيت أناكوندا مع بيثون 3.7 على النظام ، ثم استخدام الأوامر التالية في المحطة الطرفية لإعداد بيئة البرمجة :
   $ كوندا إنشاء --اسم myenv بيثون = 3.7
   $ conda تنشيط myenv
   $ كوندا تثبيت اناكوندا
   $ كوندا تثبيت healpy
   ملاحظة: قد تستغرق هذه الخطوات tens دقائق استناداً إلى سرعة الأجهزة وإنترنت. يمكن تغيير اسم البيئة 'myenv' في أول سطري الأوامر إلى أي سلسلة أخرى.

2. الحصول على منحنيات ضوء متعدد الطول الموجي وهندسة المشاهدة من الملاحظات

1. في هندسة المشاهدة، تشمل خط الطول والعرض من شبه ممتاز ونقاط المراقب الفرعي لكل إطار زمني المقابلة.
   لاستخدام التعليمات البرمجية المرفقة التالية، تأكد من أن هذين الملفين لديهم نفس تنسيق LightCurve.csv و Geometry.csv.
2. تشغيل PlotTimeSeries.py لتصور البيانات والتحقق من صفاتها. سيتم إنشاء اثنين من الشخصيات LightCurve.png والهندسة.png (الرقم التكميلي 1-2). قد تحتاج المعلمات في هذا و رموز الرسم التالية إلى ضبط إذا تم تطبيقها على ملاحظات مختلفة.
   $ بيثون PlotTimeSeries.py لايتكوريف
   هندسة PlotTimeSeries.py الثعبان

3. استخراج المعلومات السطحية من منحنيات الضوء

1. مركز الوقت التي حلها متعددة الطول الموجي منحنيات ضوء albedo من كوكب خارجي وتطبيعها عن طريق الانحراف المعياري المقابلة في كل طول موجي. وهذا يؤدي إلى الأهمية المتساوية لكل قناة.
   
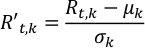
   حيث_{R't, ك} و R_t,k هي albedo تحجيم ولاحظ في الخطوة t-th الوقت و ك الطول الموجي, على التوالي; μ_ك و σ_ك هي الانحراف المتوسط والياري لسلسلة الزمن albedo في الطول الموجي ك th.
   1. تشغيل Normalize.py لتطبيع منحنيات الضوء، R_t،k. يتم حفظ الإخراج في تطبيعLightCurve.csv.
      80 دولار Normalize.py بيثون
2. تشغيل PlotTimeSeries.py لتصور منحنيات الضوء تطبيع. سيتم إنشاء شخصية NormalizedLightCurve.png (الشكل التكميلي 3).
   $ بيثون PlotTimeSeries.py تطبيعLightCurve
3. تطبيق SVD على منحنيات ضوء albedo تحجيم للعثور على أجهزة الكمبيوتر المهيمنة وسلسلة زمنية المقابلة لها.
   
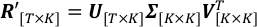
   على الجانب الأيسر، T وK هي العدد الإجمالي للخطوات الوقت وأطوال موجية للمراقبة; R' هو مصفوفة من الملاحظات albedo تحجيم، الذي (ر، ك) th العنصر هو_R't،k. على الجانب الأيمن، أعمدة V هي أجهزة الكمبيوتر، vectors أو متعامدة التي تحدد مشاريع SVD الفضاء إلى; Σ هو مصفوفة قطرية، عنصرها (ك، ك) th هو الانحراف المعياري من المنحنيات الخفيفة تحجيم على طول محور k-th التي يحددها العمود ك- th من V؛ أعمدة U هي سلسلة الوقت المقابلة لكل جهاز كمبيوتر في V.
   1. تشغيل SingularValueDecomposition.py لتتحلل R'. يتم حفظ Uالناتجة ، Σ، V^T في ملفات الإخراج U.csv، SingularValue .csv و V_T.csv، على التوالي.
      800 دولار SingularValueDecomposition.py بيثون
4. استخدم PlotTimeSeries.py PlotSVD.py لتصور نتيجة SVD. ثلاثة أرقام U.png، سيغما.png V_T.png وسيتم إنشاء(الرقم التكميلي 4-6).
   $ بيثون PlotTimeSeries.py يو
   PlotSVD.py بيثون دولار
5. تحليل المساهمات وسلسلة زمنية مقابلة من أجهزة الكمبيوتر لتحديد واحد الذي يحتوي على معلومات سطحية.
   1. قارن بين القيم المفردة عند قطري Σ. ومن المتوقع أن يكون للكواكب الخارجية الغائمة جزئياً الشبيهة بالأرض قيمتان متماثلتان مُنفردتان مُقارنتان.
      ملاحظة: قد تحتوي Σ على قيمتين مفردتين مهيمنتين أو أكثر، وهو ما تتم مناقشته أدناه.
   2. قارن بين أنماط السلاسل الزمنية لأجهزة الكمبيوتر المهيمنة. يميل الكمبيوتر الذي يحتوي على معلومات السطح إلى أن يكون الشكل أكثر انتظاما من الآخر. بسبب عدم التماثل الطولي وظهور السطح مع تغيرات صغيرة في يومين متتاليين ، تميل السلسلة الزمنية المقابلة إلى أن يكون لها تباين يومي ثابت تقريبًا.
   3. حساب الدوّات الدورية لاثنين من أجهزة الكمبيوتر المهيمنة باستخدام لومب سكارجل^{910 ،}لتأكيد اختيار جهاز الكمبيوتر. يميل الكمبيوتر الذي يحتوي على معلومات سطحية إلى أن يكون أعلى الذروة المقابلة لفترة التناوب في الطيف كثافة الطاقة.
   4. تشغيل Periodogram.py للحصول على أطياف الطاقة من سلسلة الوقت من كل جهاز كمبيوتر. يتم حفظ أطياف الطاقة في منظار الالوغرام.csv.
      800 دولار Periodogram.py
   5. تشغيل PlotPeriodogram.py لتصور هذه العصور الزمنية وتأكيد اختيار جهاز الكمبيوتر. سيتم إنشاء رسم اجسام اغراء.png (الشكل التكميلي 7). تضيف التعليمات البرمجية للرسم الحالية في خطوط متقطعة تمثل دورات سنوية ونصف سنوية ويومية ونصف يومية كمرجع، والتي قد تحتاج إلى تغيير عند تطبيقها على ملاحظات أخرى.
      80 PlotPeriodogram.py بيثون دولار
   6. حدد PC، V_ي،الذي يحتوي على المعلومات السطحية وسلسلة الوقت، ش_ي.
      
      
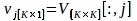
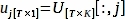
      حيث V[: ، ي ] وU[: ، ي] هي الأعمدة ي - th من V وU، على التوالي ؛ ي هو مؤشر الكمبيوتر الاستدلال في الخطوة 3.3 التي تحتوي على معلومات السطح.

4. بناء خريطة سطح الكواكب

1. استخدم أسلوب^{11 11 11} بكسل 11 (HEALPix) في منطقة متساوية هرمية. يقسم السطح الكروي لكوكب إلى بيكسل بنفس المساحة والتوزيع الموحد. الإشارة إلى القيمة غير المعروفة للبكسل p-th كـ x_p.
   1. تشغيل HEALPixRandom.py لتصور أسلوب البكسل. وسيتم إنشاء الرقم HEALPixRandom.png (الرقم التكميلي 8). يمكن تغيير_{المعلمة N الجانب} في سطر 17 لمختلف القرارات. قد تستغرق هذه الخطوة بضع ثوانٍ إلى دقائق استناداً إلى الدقة.
      HEALPixRandom.py بيثون دولار
2. حساب وزن p-th بكسل في الملاحظات في الخطوة t-th الوقت، ث_{t، ع،}باستخدام هندسة العرض.
   
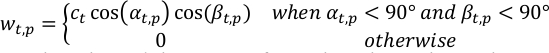
   حيث α_t,p,β_t,p هي الشمسية وزوايا ذروة المركبة الفضائية في p-th بكسل في الخطوة t-th الوقت; c_t عبارة التطبيع من t-th الملاحظة بحيث مجموع الوزن الكلي في كل خطوة الوقت هو الوحدة.
   ملاحظة: يفترض الهندسة أن تكون معروفة في هذه الخطوة أو يمكن أن يكون مشتق من تحليل آخر الذي تتم مناقشته أدناه.
   1. تشغيل ComputeWeight.py لحساب w_{t, p}. تغيير قيمة_جانب N في سطر 23 لدقات أخرى من مخطط استرداد. يتم حفظ الإخراج كـ W.npz بسبب حجمه.
      ComputeWeight.py بيثون دولار
3. استخدم PlotWeight.py لتصور هذه الأوزان. سيتم إنشاء عدد من الأرقام، واحدة في كل خطوة من الوقت، في مجلد الوزن. يؤدي دمجها إلى فيديو تكميلي 1، والذي يوضح كيفية تغير وزن كل بكسل مع مرور الوقت. قد تستغرق هذه الخطوة ساعات لإنهاء نظراً لعدد كبير من المرئيات.
   800 دولار PlotWeight.py بيثون
4. الجمع بين الهندسة والملاحظات للوصول إلى مشكلة الانحدار الخطي.
   
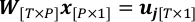
   حيث P هو العدد الإجمالي للبكسل المسترجع؛ W هو مصفوفة الوزن مع ث_{t، ع} كعنصر (t،p)-th؛ x يتكون من x_p كعنصر p-th، وهو الكمية التي يجب حلها في هذه المشكلة.
   حل مشكلة الانحدار الخطي مع تنظيم القاعدة L-2.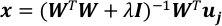
   
   حيث أنا مصفوفة الهوية وλ هو معلمة الانتظام.
   ملاحظة: 10^-3 هي قيمة جيدة لλ عندما تي ~ 10⁴ وP ~ 3 * 10³. وينبغي تعديلها بمقارنة قيم المصطلحين في الخطأ المربع المُعدن، (هـ) كما هو مبين أدناه.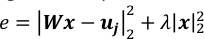
   
   1. تشغيل LinearRegression.py لحل هذه المشكلة الانحدار الخطي. يتم حفظ نتيجة x في ملف PixelValue.csv. تغيير قيمة λ في السطر 16 لنقاط القوة المختلفة للتقنية.
      LinearRegression.py بيثون دولار
5. تحويل x إلى خريطة سطح 2D وفقا لقاعدة رسم الخرائط من HEALPix.
   1. تشغيل PlotMap.py لإنشاء الخرائط المسترجعة باستخدام معلمات تنظيمية مختلفة. ثلاثة أرقام Map_-2.png، Map_-3.png Map_-4.png سيتم إنشاؤها مع الإعداد الحالي(الشكل التكميلي 9). يتم وصف العلاقة بين مؤشرات البكسل ومواقعها على الخريطة في وثيقة HEALPix¹¹. تستغرق هذه الخطوة عشرات الثواني.
      80 PolotMap.py بيثون دولار

5. تقدير عدم اليقين من الخريطة المستردة

1. أعد كتابة مشكلة الانحدار الخطي في الخطوة 4.3 مع "القيمة الحقيقية" من x كض وضوضاء المراقبة ε.
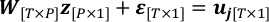
   1. افترض ε لمتابعة توزيع غاوسي N (0، σ²I_[T*T])وتقدير التباين المشترك. T-P هي درجة حرية u_j من المراقبة عند إصلاح الخريطة المسترجعة.
      
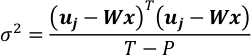
   2. دمج المعادلات في الخطوة 4.4 و 5.1. وهو يؤدي إلى متجه جاوسي من x.
      
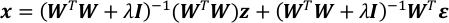
   3. حساب التوقع ومصفوفة التباين المشترك لـ x.
      
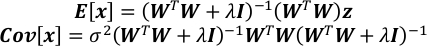
   4. الحصول على عدم اليقين من كل عنصر في x كما الجذر التربيعي للعنصر المقابل على قطري من كوف[x].
      
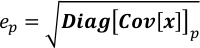
      حيث e_p هو عدم اليقين من س_ع؛ Diag[Cov[x]]_p هو عنصر p-th على قطري Cov[x].
   5. تشغيل Covariance.py لحساب مصفوفة التباين المشترك لـ x. يتم حفظ النتيجة فيOvariance.npz بسبب حجمه. تستغرق هذه الخطوة عشرات الثواني إلى الدقائق حسب حجم W.
      Covariance.py بيثون دولار
2. تحويل_ص إلى الخريطة 2D استرداد وفقا لقاعدة رسم الخرائط من HEALPix.
   1. تشغيل PlotCovariance.py لتصور كوف[س] وخريطة عدم اليقين ص_p إلى الخريطة المستردة. سيتم إنشاء اثنين من الشخصيات التباين.png وعدم اليقين.png (الشكل التكميلي 10-11).
      800 دولار PlotCovariance.py

النتائج

نستخدم منحنيات الضوء أحادية الطول متعددة الطول أحادية نقطة للأرض لإثبات البروتوكول، ونقارن النتائج مع الحقيقة الأرضية لتقييم جودة رسم الخرائط السطحية. الملاحظة المستخدمة هنا تحصل عليها DSCOVR/EPIC، وهو ساتل يقع بالقرب من أول نقطة لاغرانجية (L1) بين الأرض والشمس التي تأخذ الصور في أطوال موجية ع...

Discussion

وأحد المتطلبات الحاسمة للبروتوكول هو جدوى استخراج المعلومات السطحية من منحنيات الضوء، التي تعتمد على تغطية السحابة. في الخطوة 3.5.1، قد تختلف القيم النسبية لأجهزة الكمبيوتر الشخصية بين الكواكب الخارجية. في حالة الأرض، أول جهازي كمبيوتر تهيمن على الاختلافات منحنى الضوء، وتتوافق مع السحب ا?...

Materials

Name	Company	Catalog Number	Comments
Python 3.7 with anaconda and healpy packages			Other programming environments (e.g., IDL or MATLAB) also work.