在德布罗意发表他的想法后不久,氢原子中的电子可以更好地被认为是圆形驻波,而不是粒子在量化的圆轨道中移动,厄尔文·施罗因丁格通过推导来扩展德布罗意的工作。现在称为薛定谔方程。当薛定谔将他的方程式应用于类似氢的原子时,他能够重现能量的玻尔表达式,并由此再现控制氢谱的里德伯格公式。薛定谔将电子描述为三维固定波或波函数,由希腊字母psi(ψ )表示。
几年后,麦克斯·伯恩(Max Born)提出了对波函数ψ 的一种解释,该解释至今仍被接受:电子仍然是粒子,因此以ψ 不是物理波,而是复杂的概率振幅。波函数∣ ψ ∣ 2 的大小的平方描述了量子粒子出现在空间中某个位置附近的概率。 这意味着波函数可用于确定电子密度相对于原子核的分布。在最一般的形式中,薛定谔方程可写为:
其中,Ĥ是哈密顿算子,这是一组数学运算,表示量子粒子(例如原子中的电子)的总能量(势能和动能),&psi ; 是该粒子的波函数,可用于查找发现该粒子的概率的特殊分布,而 E  是该粒子的总能量的实际值粒子。
薛定谔的工作以及海森堡和许多其他科学家紧随其后的工作,通常被称为量子力学。
量子力学模型将轨道描述为原子内原子核周围的三维空间,在其中发现电子的概率最高。
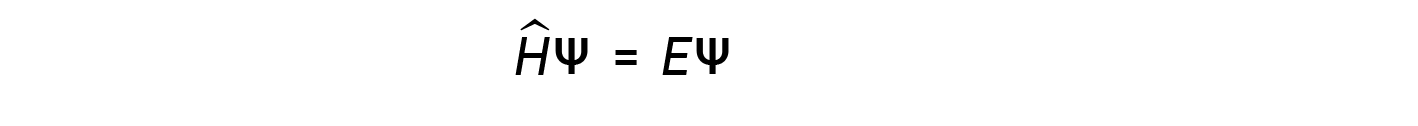
版权所属 © 2025 MyJoVE 公司版权所有,本公司不涉及任何医疗业务和医疗服务。