通过仪表AFM压痕硬度定量测量

摘要

This experimental protocol describes how atomic force microscopy can be used to measure hardness at the true nanometer scale and to detect single atomistic plasticity events.

摘要

In this work, a combination of amplitude-modulated non-contact atomic force microscopy and atomic force spectroscopy is applied for instrumented hardness measurements on an Au(111) surface with atomistic resolution of single plasticity events. A careful experimental procedure is described that includes the force sensor selection, its calibration, the calibration of the cantilever deflection detection system, and the minimization of instrumental drift for accurate and reproducible force-distance measurements. Also, a method for the data analysis is presented that allows the extraction of force-penetration curves from recorded force-distance curves. A typical curve displays a clear elastic deformation regime up to the first plasticity event, or pop-in, with a length in the range of one to two Burger's vectors. Later plasticity events exhibit the same magnitude. The work of plasticity is further extracted from the measurements. Finally, the hardness is determined in combination with the indentation curve using non-contact atomic force microscopy images of the remaining indents.

引言

For the last 150 years, hardness values have been used to characterize the mechanical behavior of materials and to predict their performance under various loading conditions. The hardness of a material describes the resistance of its surface to the penetration of a harder indenter. For metallic materials, the hardness relates to resistance to plastic flow.

Although the implementation of hardness testing has proven to be relatively easy, the yielded results have long been rather empirical, making them unable to describe the intrinsic properties of the investigated material. The empirical nature of hardness testing results has been a consequence of the use of various indenter geometries, each of which has a different established hardness scale. However, all empirical hardness scales, such as the Brinell hardness (HB) test for spherical indenters and the Vickers (HV) and Knoop (HK) hardness tests for different types of four-sided pyramids, have one thing in common: the hardness number is determined from the ratio of the applied load to the developed area of the remaining indent. In an attempt to relate the hardness of metals to their fundamental mechanical properties, the hardness measured with a spherical indenter has been defined as the ratio of the applied load to the projected area of the remaining indent. This hardness value, also known as the Meyer's hardness (H), is equal to the mean contact pressure and directly relates to the yield strength of non-work-hardening metals¹.

Hardness testing has long been limited to the macro-scale, in which case the sizes of indents have been measured by optical means. The development of instrumented indentation, where force-displacement curves are recorded, has been recognized as a valuable alternative for determining the hardness of a material, although the size of the remaining indent may be too small to be accurately imaged. In this case, the projected area of the indent is calculated from the tip displacement according to a so-called indenter-area function². Due to this development, the analysis of the curvature of force-displacement curves and of the occurrence of distinct plasticity events in the shape of pop-ins is now widely used to study the mechanisms of plastic deformation at the micrometer scale, such as by means of nanoindentation³.

It is well accepted that the carriers of plastic deformation in metals, i.e., dislocations, operate at the nanometer scale. To understand their modes of operation at the atomic level, new experimental techniques with atomic resolution are needed. Initial investigations of atomistic plasticity events at the interfaces between nanometer-sized single asperities and single crystalline Au surfaces of different orientations have been carried out by interfacial force microscopy (IFM)^{4, 5}. Atomic force microscopy (AFM) indentation has been applied to observe the nucleation and gliding of single dislocations in KBr(100) single crystals⁶, Cu(100)⁷, and Au(111)^{8, 9}. There, atomistic plasticity events were observed in the shape of pop-ins, with lengths in the range of 1 Å. AFM indentation has also been used to measure the nano-hardness and -elasticity of gold nano-island grown on mica¹⁰. In this work, the nano-hardness was found to be smaller than the bulk value and was observed to depend linearly on the indentation area. Also, a detailed measurement protocol has been proposed to determine the hardness of hard surfaces, such as fused quartz and silicon, by AFM indentation with a diamond-tipped sapphire cantilever¹¹. In particular, this method takes into account the non-linearity of the photo-sensitive deflection detectors for large cantilever deflection¹². More recently, AFM indentation and non-contact AFM imaging have been combined to quantitatively determine the hardness and the fundamental mechanisms of plastic deformation of a Pt(111) single crystalline surface and Pt-based metallic glass¹³. For Pt(111), plastic deformation mechanisms at the nanometer scale were found to be consistent with the discrete mechanisms established for larger scales. Further, the nanometer-scale plastic deformation of the metallic glass was found to be not discrete, but rather continuous and highly localized around the indenting tip. These results revealed a lower size limit for metallic glasses, below which shear transformation mechanisms are not activated by indentation. AFM indentation has also been used to determine the hardness values of biological samples (such as collagen fibrils)¹⁴, polymers¹⁵, and colloidal crystals¹⁶.

In the present work, a careful experimental procedure is described that includes the force sensor selection, its calibration, the calibration of the cantilever deflection detection system, and the minimization of instrumental drift for accurate and reproducible force-distance measurements. Also, a method for the data analysis is presented that allows the extraction of force-penetration curves from recorded force-distance curves. Further representative results are shown and discussed in the light of recent findings in the field of plastic deformation of small volumes.

For this experiment, an atomic force microscope (AFM) was used. The cornerstone of an AFM is its micro-fabricated force sensor (usually a cantilever beam), with a sharp tip at the end whose radius is in the range of several nanometers. In the particular configuration of the instrument used for this experiment, the cantilever is mounted onto a piezo-electric z-scanner, while the sample to be investigated is mounted onto a piezo-electric x/y-scanner. During AFM imaging, the force sensor tip is scanned over a sample to register interaction forces with the sample surface that result in a deflection of the cantilever according to Hooke's law. The static or dynamic deflection of the cantilever can be measured with an optical beam deflection detector, consisting of a laser diode, a set of mirrors, and a photodiode that converts the cantilever deflection into a voltage. During imaging, the signal at the photodiode is controlled by a feedback loop so as to keep the interaction forces at the sample surface; this results in adjustments of the z-scanner position, which are recorded and displayed as a topography image.

Prerequisites for the experiment described below are that the piezo-electric scanners of the atomic force microscope are well-calibrated and that the instrument stays in the laboratory at a constant temperature and humidity level. The reader should be aware that, depending on the atomic force microscope model, some of the experimental procedure steps may have to be modified. In particular, all measurements are performed after setting the scanners' ranges to "small"; this function allows for the reduction of the x/y-scanner range to 5 x 5 µm² and the z-scanner range to 4 µm, which ensures a resolution at small scales. This function is not available on all commercial AFM and is not mentioned in the remainder of the text.

For data analysis, the use of the free SPM data analysis software Gwyddion¹⁷ and the Matlab software package¹⁸ are recommended.

This protocol gives a description of the experimental procedure to be followed in order to perform instrumented hardness measurements by AFM. Since the handling of different commercial AFMs may differ from one model to the other, the reader should refer to the manual provided by the AFM manufacturer for detailed setting procedures and software information. In the following text, in order to reproduce the described experiment, it is assumed that the reader is familiar with the handling of the particular AFM used here.

研究方案

1.仪器设置和校准

1. 仪器的建立
   1. 使用类型DT-NCLR或CDT的NCLR的僵硬金刚石涂层悬臂具有第一自由共振频率f _0,1≥180千赫，一个品质因数Q≥300和弯曲刚度ķ≥40牛顿/米。
   2. 装入选定悬臂上通过AFM制造商提供的夹紧座。要特别小心放置的悬臂，使得其长轴垂直于AFM的快速扫描方向。另外，胶悬臂梁上用双组分环氧胶的原子力显微镜制造商提供的悬臂支架。
   3. 安装悬臂支架上AFM头，并使用通常可用的AFM系统的光学显微镜集中于AFM悬臂。仔细检查悬臂的长轴垂直于快速扫描方向。如果没有，回去第1.1.2节。
   4. 对准的激光束，以便它在悬臂的端部反射。监视在光电二极管上的电压总和，并进行微调，以最大限度地提高和信号。典型的和信号的值是在2伏的范围内
   5. 调整反射镜的水平和垂直的倾斜角度，以便使反射的激光点进入光电二极管，其中，对应于垂直和横向位移的电压几乎为零的中心。
2. 校准
   1. 执行一个频率扫描，以确定所述第一自由弯曲谐振F中的悬臂的_0,1。
   2. 确定悬臂k的弯曲刚度，根据¹⁹计算出
      （1）
      其中E是杨氏模量，L为悬臂的长度，w是cantil的宽度以往，t是其厚度。为此目的，测量由光学显微镜或扫描电子显微镜的悬臂的长度和宽度具有更高的精度。从其第一自由弯曲共振频率计算悬臂的厚度_˚F0,1，根据
      （2）
      其中ρ是质量密度。
   3. 选择用于特定悬臂型的光电二极管的灵敏度的缺省值以用于在AFM中的设置菜单中的实验。通过点击按钮的方式带来悬臂尖端与参考样本接触的负荷F _N = 10 NN。
   4. 打开在AFM软件的力谱菜单和与z扫描器的相对缩回和延伸设置为50nm，并且在z扫描器缩回/延伸至0.3微米/秒。这样，力 - 距离曲线的记录会由第一与z扫描器至50纳米从样品表面离开，然后一系列相同的距离的方法和撤消的回缩。
   5. 记录与在1.2.4建议在光滑和不符合要求的表面所设置的参数，如纳米晶金刚石或蓝宝石的力距离曲线，以避免样品变形效果。要做到这一点点击在AFM软件的力量光谱菜单中的采集按钮。
   6. 适合的力 - 距离曲线的推斥力部分具有线性函数，在AFM中软件的校准菜单。嵌合线的逆斜率对应于光电二极管灵敏度S。通过点击执行校准按钮代替确定的值，以在AFM软件的校准菜单仪器软件的默认值。

2.样品制备

注:THI测量样品小号实验由一个100-nm厚，原子级平滑的Au（111）薄通过物理气相沉积生长在云母膜构成。

1. 装入样品到由双面碳胶带的装置由仪器制造商提供的磁性样品架。为了避免在测量过程中样品的漂移，装入样品一天测量之前，以便让碳胶带放松。可替代地，安装样本上银漆，通常在几分钟之内干燥的持有人。
2. 安装磁性样品架到X / Y扫描仪。

3.测量步骤

1. 略设定振荡频率偏共振（在此实验中F = 190.67千赫），并在A = 20纳米注振荡幅度，这些数值是由仪器软件此特定悬臂自动设置。 在_设定点 = 5纳米手动设置振荡设定点。
2. 画悬臂朝向使用原子力显微镜的步进电机样品表面。确保该力传感器不与样品表面碰撞。请重点悬臂粗进近过程中，并停止粗的办法之前，样品表面是在完美的焦点。
3. 通过点击的方式按钮自动接近力传感器。一旦振荡幅度已经达到其设定点，尖端准备扫描样品表面的形貌。
4. 上记录的区域范围从5×5到1×1平方微米的一系列地形图像（如果有的话，通过倾斜的x / y扫描器调整地形信号的斜率）。确保同一地区的连续图像不显示漂移的迹象，而且Z扫描器位置几乎保持不变。如果不是这种情况下，继续成像直到系统已经稳定。
5. 一旦系统已经稳定，平滑的1×1平方微米面积已经发现，收回的F奥尔塞通过点击回缩按钮传感器从样品表面上的几微米。
6. 选择在仪器菜单的力谱模式和移动力传感器预选1×1平方微米区域的中间，以10nm的力设定点。监视的z扫描器的位置，直到它保持不变。
7. 选择，其中心对应于预选1×1平方微米区域的中心点的2×2的网格。在500nm设置两个下相邻点之间的距离。
8. 设置相对扫描器的距离为0到150纳米，在300纳米/秒的速度变化，并随后缩回过相同的距离，并以相同的速度。给定悬臂的倾斜角相对于所述样品表面上，由一个垂直扫描器扩展Z，其中φ是倾斜角²⁰期间移动由Z横向扫描器×黄褐色φ施加倾斜校正。
   注:一些研究所ruments占其力光谱法或压痕模式悬臂倾斜;这是在这项工作中使用的原子力显微镜的情况。
9. 按下仪器软件启动按钮，开始收购AFM压痕数据。
10. 一旦AFM压痕测量已经完成时，缩回力传感器从样品表面几微米远。
11. 选择在仪器软件菜单的非接触型的AFM模式成像和重复在第3.1和3.2中描述的方法。
12. 执行过相同的1×1平方微米面积的扫描如第3.3节，以找到缩进的精确位置。在一个500×500纳米2表面积进一步的表面扫描，可以更详细地进行图像其余缩进。

4.数据分析

1. 图像处理
   1. 处理所记录的形貌的图像，以便使其在快速扫描目录的线基于中值差挠度。使用Gwyddion的内置函数。
2. 计算投影面积使用Gwyddion的压痕分析功能缩进的_页 。
3. 通过使用Gwyddion的尖端分析功能估算缩进的地形图像针尖形状。然后平均尖端形图像，并测量平均前端形状的半开口角α。
4. 通过根据¹³计算尖端位移δ转换力-距离曲线生效位移曲线
   （3）
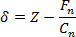
   其中Z是相对的扫描仪的位置。
5. 现在，绘制力与尖端位移。所得曲线通常显示所谓弹出插件，与长度在几个100微米的范围内，对应于原子可塑性事件。使用第一个THES的Ë弹出插件，以确定在弹性限度_δEL ⁴尖端位移。
6. 适合与赫兹功能²¹的力-位移曲线的弹性部分。
   （4）
   其中R是尖端半径和^E'*是弹性模量减小，由下式给出 ，其中M _S，T是样品和尖端的压痕模，分别。在这种情况下，拟合参数是 。
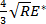7. 延伸拟合函数成可塑性制度，以便从拟合函数和实验曲线²¹之间的面积差来计算塑性W¯¯ _可塑性的工作。
8. 根据¹计算样品的硬度^，2
   （5）
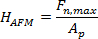
   和
   （6）
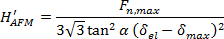
   其中，F _N，max是最大施加载荷，A _p是在4.2节计算缩进的投影面积，α是在4.3节算出的末端的半开度角，δ _埃尔处于第一可塑性尖端位移事件， _最大 δ是最大位移尖（参见4.4节）。

结果

在这项工作中，悬臂k的弯曲刚度根据几何梁理论¹⁹计算。在这项工作中所用的特定金刚石涂覆悬臂，我们发现K = 55.69牛顿/米。需要注意的是我们忽略了金刚石涂层;金刚石涂层的厚度是一个数量级比悬臂厚度小两个数量级，因此不显著增加其弯曲刚度（虽然它的杨氏模量是比硅的显著大）。

为了避免样品?...

讨论

的方法，已提出了用金刚石涂覆AFM针尖上的Au（111）执行一系列压痕薄膜表面。非接触式的AFM成像和原子力显微镜压痕用相同的力传感器进行的。用于非接触成像的要求是很高的第一自由共振频率f _0,1≥180千赫和高品质因数Q≥300。在AFM压痕，要施加的垂直力在几个微牛顿的范围内，并具有高的弯曲刚度悬臂是必需的。该悬臂刀片的附加要求是，它是机械上稳定的和耐磨。这些...

材料

Name	Company	Catalog Number	Comments
AFM XE-100	Park Instruments	discontinued	Atomic force microscope
CDT-NCLR	NanoSensors	CDT-NCLR	Conductive diamond coated non-contact lever
100 nm thick Au(111) thin film on Mica	Phasis	20020011	atomically smooth gold thin film