Strukturbasierte Simulation und Probenahme von Transkriptionsfaktor-Proteinbewegungen entlang der DNA vom atomaren Schritt bis zur grobkörnigen Diffusion

Zusammenfassung

Das Ziel dieses Protokolls ist es, die strukturelle Dynamik der eindimensionalen Diffusion von Protein entlang der DNA unter Verwendung eines pflanzlichen Transkriptionsfaktors WRKY-Domänenprotein als beispielhaftes System aufzudecken. Zu diesem Zweck wurden sowohl atomistische als auch grobkörnige Molekulardynamiksimulationen zusammen mit umfangreichen computergestützten Stichproben implementiert.

Zusammenfassung

Das eindimensionale (1-D) Gleiten des Transkriptionsfaktors (TF)-Proteins entlang der DNA ist essentiell für die erleichterte Diffusion der TF, um die Ziel-DNA-Stelle für die genetische Regulation zu lokalisieren. Der Nachweis der Base-Pair-Auflösung (bp) des TF-Gleitens oder -Tretens auf der DNA ist immer noch eine experimentelle Herausforderung. Wir haben kürzlich All-Atom-Molekulardynamik-Simulationen (MD) durchgeführt, die spontanes 1-bp-Stepping eines kleinen WRKY-Domänen-TF-Proteins entlang der DNA erfassen. Basierend auf dem 10 μs WRKY-Schrittpfad, der aus solchen Simulationen gewonnen wurde, zeigt das Protokoll hier, wie umfangreichere Konformationsproben der TF-DNA-Systeme durchgeführt werden können, indem das Markov-Zustandsmodell (MSM) für das 1-bp-Protein-Stepping konstruiert wird, wobei verschiedene Mikro- und Makrozustände für die MSM-Konstruktion getestet wurden. Um die prozessive 1-D-Diffusionssuche des TF-Proteins zusammen mit DNA mit struktureller Basis zu untersuchen, zeigt das Protokoll außerdem, wie grobkörnige (CG) MD-Simulationen durchgeführt werden können, um die langfristige Skalendynamik des Systems zu untersuchen. Solche CG-Modellierungen und -Simulationen sind besonders nützlich, um die elektrostatischen Auswirkungen der Protein-DNA auf die prozessiven Diffusionsbewegungen des TF-Proteins über Dutzende von Mikrosekunden aufzudecken, im Vergleich zu Submikrosekunden bis Mikrosekunden Proteinschrittbewegungen, die aus den Allatomsimulationen aufgedeckt wurden.

Einleitung

Transkriptionsfaktoren (TF) suchen nach der Ziel-DNA, um die Gentranskription und die damit verbundenen Aktivitäten zu binden und zu regulieren¹. Abgesehen von der dreidimensionalen (3D) Diffusion wurde vorgeschlagen, dass die erleichterte Diffusion von TF für die Ziel-DNA-Suche unerlässlich ist, bei der die Proteine auch entlang eindimensionaler (1D) DNA gleiten oder hüpfen oder mit intersegmentalem Transfer auf die DNA^{springen können} 2,3,4,5,6,7.

In einer kürzlich durchgeführten Studie haben wir Dutzende von Mikrosekunden (μs) All-Atom-Gleichgewichtsmolekulardynamik (MD) -Simulationen an einer pflanzlichen TF durchgeführt - dem WRKY-Domänenprotein auf der DNA⁸. Ein vollständiges 1-bp-Stepping von WRKY auf Poly-A-DNA innerhalb von Mikrosekunden wurde aufgenommen. Die Bewegungen des Proteins entlang der DNA-Rille und der Breaking-Reforming-Dynamik von Wasserstoffbrückenbindungen (HBs) wurden beobachtet. Während eine solche Trajektorie einen abgetasteten Pfad darstellt, fehlt es immer noch an einer allgemeinen Protein-Stepping-Landschaft. Hier zeigen wir, wie mit dem konstruierten Markov-Zustandsmodell (MSM) rechnerische Stichproben um den anfänglich erfassten Proteinschrittpfad erweitert werden können, die für die Simulation einer Vielzahl von biomolekularen Systemen mit erheblichen Konformationsänderungen und Zeitskalentrennung weit verbreitet sind 9,10,11,12,13,14,15,16^{. 17,18,19}. Ziel ist es, das Konformationsensemble und die metastabilen Zustände der TF-Proteindiffusion entlang der DNA für einen zyklischen Schritt aufzudecken.

Während die obige MD-Simulation die atomare Auflösung der Proteinbewegungen für 1 bp auf der DNA zeigt, ist die strukturelle Dynamik der langzeitprozessiven Diffusion der TF entlang der DNA bei der gleichen hohen Auflösung kaum zugänglich. Die Durchführung von grobkörnigen (CG) MD-Simulationen auf Rückstandsebene ist jedoch technisch zugänglich. Die CG-Simulationszeitskala kann effektiv auf das Zehn- oder Hundertfache verlängert werden als die atomaren Simulationen 20,21,22,23,24,25,26,27,28,29. Hier zeigen wir die CG-Simulationen, die durch die Implementierung der von Takada lab³⁰ entwickelten CafeMol-Software durchgeführt wurden.

Im aktuellen Protokoll präsentieren wir zuerst die atomaren Simulationen des WRKY-Domänenproteins entlang der Poly-A-DNA und die MSM-Konstruktion, die sich auf die Probenahme der Proteinschrittbewegungen für nur 1 bp entlang der DNA konzentrieren. Dann präsentieren wir die CG-Modellierung und Simulationen desselben Protein-DNA-Systems, die die rechnerische Probenahme auf die proteinprozessive Diffusion über Dutzende von bps entlang der DNA ausdehnen.

Hier verwenden wir die Software GROMACS 31,32,33, um MD-Simulationen durchzuführen, und MSMbuilder^34, um das MSM für abgetastete Konformationsschnappschüsse zu konstruieren und VMD ³⁵ zur Visualisierung der Biomoleküle zu verwenden. Das Protokoll erfordert, dass der Benutzer in der Lage ist, die oben genannte Software zu installieren und zu implementieren. Die Installation und Implementierung der CafeMol 30-Software ist dann für die Durchführung der CG^{MD-Simulationen} erforderlich. Weitere Analysen der Trajektorien und Visualisierungen werden ebenfalls in VMD durchgeführt.

Protokoll

1. Aufbau des Markov-Zustandsmodells (MSM) aus atomaren MD-Simulationen

1. Spontaner Proteinschrittweg und anfängliche Struktursammlung
   1. Verwenden Sie eine zuvor erhaltene 10-μs-Allatom-MD-Trajektorie^8, um 10000 Frames gleichmäßig aus einem "vorwärts" 1-bp-Schrittpfad (d. h. einem Frame für jede Nanosekunde) zu extrahieren. Die Gesamtzahl der Frames muss ausreichend groß sein, um alle repräsentativen Konformationen einzubeziehen.
   2. Bereiten Sie den Übergangspfad mit 10000 Frames in VMD vor, indem Sie auf Datei > Klicken Sie auf Datei Speichern Sie Koordinaten, geben Sie Protein oder Nukleinsäure in das Feld Ausgewählte Atome ein, wählen Sie Frames im Feld Frames aus, klicken Sie auf Speichern , um die benötigten Frames abzurufen.
      HINWEIS: Eine zuvor erhaltene 10 μs All-Atom MD-Simulationstrajektorie (hier "Forward Stepping Trajektorie" genannt) für WRKY stepping 1-bp Abstand auf einer 34-bp homogenen Poly-A DNA⁸ wurde als erster Weg verwendet, um weitere Konformationsproben zu starten. Beachten Sie, dass in den meisten Praktiken jedoch ein anfänglicher Pfad konstruiert wird, indem gesteuerte oder gezielte MD-Simulationen durchgeführt oder allgemeine Pfadgenerierungsmethoden usw. implementiert werden.36,37,38,39.
   3. Richten Sie die Längsachse der Referenz-DNA (von der Kristallstruktur) an der x-Achse aus und legen Sie den Anfangsmassenschwerpunkt (COM) der vollständigen 34-bp-DNA am Ursprung des Koordinatenraums fest, um die weitere Datenanalyse zu erleichtern. Klicken Sie dazu in VMD auf Erweiterungen > Tk-Konsole und geben Sie im Befehlsfenster Tk-Konsole Folgendes ein:
      Quelle rotate.tcl
      Das tcl-Skript finden Sie in der Zusatzdatei 3.
   4. Berechnen Sie dann den Wurzel-Mittelwert-Quadratabstand (RMSD) des Proteinrückgrats, indem Sie die zentrale 10-bp-DNA (A 14 bis 23 und T 14' bis 23') an der aus der Kristallstruktur⁴⁰ ausrichten, und die RMSD stellen geometrische Maße der Systeme dar (siehe Abbildung 1A). Klicken Sie dazu auf VMD > Erweiterungen > Analyse > RMSD-Trajektorienwerkzeug und geben Sie Nukleie und Rückstand 14 bis 23 und 46 bis 55 in das Atomauswahlfeld ein, klicken Sie auf Ausrichten und dann auf das Feld RMSD, um die RMSD-Werte zu berechnen.
   5. Berechnen Sie den Rotationsgrad des Proteins um DNA Θ(t) auf der y-z-Ebene in MATLAB, indem Sie den Befehl
      rad2deg(atan(z/y))
      wobei die anfängliche Winkelpositionierung als Θ(0)=0 definiert ist, wie zuvor⁸ durchgeführt.
   6. Geben Sie den folgenden Befehl in MATLAB⁴¹ ein, um die K-Means-Methoden^42,43,44 zu verwenden und die 10000 Strukturen durch Eingabe in 25 Cluster zu klassifizieren:
      [idx, C]=kmeans( X, 25)
      hier ist X eine 2D-Matrix von RMSD und Rotationswinkel von WRKY auf der DNA. Sammeln Sie die Strukturen dieser 25 Clusterzentren für weitere MD-Simulationen.
      HINWEIS: Da das Protein RMSD, das relativ zur DNA beprobt wird, einen Bereich von etwa 25 Å abdeckt, wählen wir 25 Cluster aus, um einen Cluster pro Angstrom zu haben.
2. Durchführung der 1^. Runde der MD-Simulationen und der Simulationseinstellungen
   1. Erstellen Sie atomistische Systeme für die 25 Strukturen, indem Sie die GROMACS 5.1.2-Software³² unter dem Parmbsc1-Kraftfeld⁴⁵ verwenden und die buildsystem.sh-Datei aus der Zusatzdatei 2 in der Schale verwenden.
   2. Führen Sie 60-ns-MD-Simulationen für diese 25 Systeme unter NPT-Ensemble mit einem Zeitschritt von 2 fs durch, indem Sie den folgenden Befehl in die Shell eingeben:
      gmx_mpi grompp -f md.mdp -c npt.gro -p topol.top -o md.tpr
      gmx_mpi mdrun -deffnm MD
3. Clustern der 1^St Runde MD-Trajektorien
   1. Entfernen Sie die ersten 10 ns jeder Simulationstrajektorie, indem Sie in shell eingeben:
      gmx_mpi trjcat -f md.xtc -b 10000 -e 600000 -o newtraj.xtc
      und sammeln Konformationen aus den 25 × 50 ns Trajektorien für das Clustering, um die Eingabestrukturen für die nachfolgenden umfangreicheren Stichproben vorzubereiten (MD-Simulationen der 2^. Runde).
      HINWEIS: Um die Auswirkungen des anfänglichen Pfades zu reduzieren und ein lokales Gleichgewicht zu ermöglichen, wurden 10 ns der Anfangsphase der Simulationen entfernt.
   2. Wählen Sie Entfernungspaare zwischen Protein und DNA als Eingabeparameter für die Projektion der zeitunabhängigen Komponentenanalyse (tICA)^46,47,48. Verwenden Sie dazu den Befehl make_ndx in GROMACS:
      gmx_mpi make_ndx -f Eingabe.pdb -o index.ndx
      HINWEIS: Hier wurden die Protein-CA-Atome und die schweren Atome (NH1, NH2, OH, NZ, NE2, ND2) des Rests Y119, K122, K125, R131, Y133, Q146, K144, R135, W116, R117, Y134, K118, Q121 ausgewählt, die Wasserstoffbrückenbindungen (HBs) mit dem DNA-Nukleotid bilden können, die sich mit den O1P O2P- und N6-Atomen des DNA-Nukleotids (A14-20, T19-23). Die ausgewählten Aminosäuren können entweder stabile HBs bilden oder Salzbrücken mit DNA bilden.
   3. Kopieren Sie den oben ausgewählten Atomindex aus der Datei index.ndx in eine neue Textdatei (index.dat). Holen Sie sich die Paarinformationen zwischen diesen Atomen mit dem Python-Skript aus Supplementary File 1 generate_atom_indices.py und geben Sie Folgendes ein:
      python2.6 generate_atom_indices.py index.dat > AtomIndices.txt
      Dadurch entstehen die 415 Entfernungspaare zwischen Protein und DNA.
   4. Berechnen Sie die 415 Entfernungspaare aus jeder Trajektorie, indem Sie den folgenden Befehl in das MSMbuilder-Befehlsfenster eingeben:
      msmb AtomPairsFeaturizer -out pair_features --pair_indices AtomIndices.txt --top references.pdb --trjs "trajectories/*.xtc" --transformierte pair_features --Schritt 5
   5. Führen Sie tICA durch, um die Dimension der Daten auf die ersten 2 zeitunabhängigen Komponenten (tICs) oder Vektoren zu reduzieren, indem Sie Folgendes eingeben:
      msmb tICA -i .. /tica_rc_a/tmp/ -o tica_results --n_components 2 --lag_time 10 --gamma 0,05 -t tica_results.h5
      HINWEIS: tICA ist eine Dimensionsreduktionsmethode, die den Eigenwert der zeitverzögerten Korrelationsmatrix berechnet,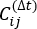 um die langsamsten entspannenden Freiheitsgrade des Simulationssystems durch die Gleichung zu bestimmen: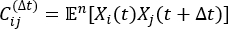
      
      wobei X i(t) der Wert der _i-ten Reaktionskoordinate zum Zeitpunkt t und X j(t+Δ t) der Wert der _j-ten Reaktionskoordinate zum Zeitpunkt t+Δ t ist.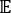 ist der Erwartungswert des Produkts der Gesamtsimulationstrajektorien X _i(t) und X_j(t +Δ t). Die Richtungen entlang der langsamsten Entspannungsgrade entsprechen den größten Eigenwerten der obigen zeitverzögerten Korrelationsmatrix. 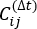Hier scheinen 2 tICs ein minimaler Satz zu sein, um drei Makrozustände auf unserer MSM-Konstruktion zu unterscheiden (später angesprochen). Man kann auch den verallgemeinerten Matrix-Rayleigh-Quotienten (GMRQ) -Score⁴⁹ berechnen, um beispielsweise einen optimalen Satz von Komponenten zu untersuchen, die verwendet werden sollen.
   6. Verwenden Sie den Befehl in MSMbuilder, um die projizierten Datasets mit der K-center^{43,44-Methode} in 100 Clustern zu gruppieren (siehe Abbildung 1B):
      msmb KCenters -i ./tica_results.h5 -o kcenters_output -t kcenters_output --n_clusters 100.
      Wählen Sie die Mittelstruktur jedes Clusters als Ausgangsstruktur für die 2. Runde der MD-Simulationen^aus. Pflegen Sie die Simulationsinformationen der simulierten 100 Strukturen, einschließlich Positionen, Temperaturen, Drücke usw., mit Ausnahme der Geschwindigkeiten.
      HINWEIS: Nach der ersten Runde von 25 Simulationen wurde der Speicher des anfänglichen Pfades reduziert, so dass wir in der zweiten Runde mehr Cluster, z. B. 100 Cluster, generieren, um die Konformationsstichproben erheblich zu erweitern.
4. Durchführung der 2^. Runde umfangreicher MD-Simulationen
   1. Führen Sie 60-ns-MD-Simulationen durch, beginnend mit diesen 100 Anfangsstrukturen, nachdem Sie allen Atomen zufällige Anfangsgeschwindigkeiten auferlegt haben. Fügen Sie die zufälligen Anfangsgeschwindigkeiten hinzu, indem Sie die Geschwindigkeitsgenerierung in der mdp-Datei aktivieren, d.h. die md.mdp-Datei gen_vel = nein in gen_vel = ja ändern.
   2. Entfernen Sie die ersten 10 ns jeder Simulation, wie in Schritt 1.3.1 beschrieben, sammeln Sie 2.500.000 Snapshots von den 100 × 50 ns-Trajektorien gleichmäßig, um das MSM zu konstruieren.
      HINWEIS: Beachten Sie, dass in der späteren Makrozustandskonstruktion eine kleine Anzahl von Off-Path-Zuständen mit einer besonders niedrigen Population (~ 0,2%, auf der Unterseite der X-Θ-Ebene) gefunden wurde. Diese Off-Path-Zustände werden als ein Makrozustand klassifiziert, wenn die Gesamtzahl der Makrozustände auf 3 bis 6 festgelegt ist (Abbildung 2B). Da ein so bevölkerungsarmer Makrostat nur 3 Trajektorien umfasst, die am Ende entfernt wurden, wurden die in diesem Protokoll gezeigten Ergebnisse tatsächlich aus 97 × 50 ns Trajektorien mit insgesamt 2.425.000 Frames oder Snapshots erhalten.
5. Clustern der MD-Trajektorien der 2^. Runde
   1. Führen Sie tICA für die Trajektorien der 2. Runde wie zuvor durchgeführt^durch. Geben Sie MSMbuilder ein:
      msmb tICA -i .. /tica_rc_a/tmp/ -o tica_results --n_components 2 --lag_time 10 --gamma 0,05 -t tica_results.h5
   2. Berechnen Sie die implizite Zeitskala, um Parameter für die Korrelationsverzögerungszeit Δt und Mikrozustandszahlen zu validieren (siehe Abbildung 1C),
      
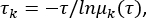
      wobei τ die Verzögerungszeit darstellt, die zum Erstellen der Übergangswahrscheinlichkeitsmatrix (TPM) verwendet wird; μ_k(τ) stellt den k-ten Eigenwert des TPM unter einer Verzögerungszeit von τ dar. Verwenden Sie das Python-Skript aus der Zusatzdatei 1 für diese Python-BuildMSMsAsVaryLagTime.py -d .. / -f .. /trajlist_num -i 50 -m 1000 -t 10 -n 20 -s 500.
   3. Variieren Sie die Verzögerungszeit τ und die Anzahl der Mikrozustände, indem Sie die oben verwendeten Parameter ändern:
      python BuildMSMsAsVaryLagTime.py -d .. / -f .. /trajlist_num -i 50 -m 1000 -t 5 10 20 30 40 -n 20 -s 20 20 200 400 500 800 2000
      HINWEIS: Das System wird als Markovian betrachtet, wenn sich die implizierten Zeitskalenkurven mit der Zeitskalentrennung einpendeln. Wählen Sie dann die Dt als Korrelationsverzögerungszeit und die τ die Verzögerungszeit, bei der sich die implizierte Zeitskala einpendelt, um MSM zu erstellen.
   4. Wählen Sie dementsprechend eine vergleichsweise große (aber nicht zu große) Anzahl von Zuständen, N = 500, und eine vergleichsweise kurze Korrelationsverzögerungszeit Δt = 10 ns. Es wurde festgestellt, dass die Verzögerungszeit τ = 10 ns für die Erstellung von MSM beträgt.
   5. Klassifizieren Sie die Konformationen in 500 Cluster (siehe Abbildung 1D), indem Sie den folgenden Befehl verwenden:
      msmb KCenters -i ./tica_results.h5 -o kcenters_output -t kcenters_output --n_clusters 500
6. MSM-Konstruktion
   1. Fassen Sie die 500 Mikrozustände in 3-6 Makrozustände zusammen, um die Anzahl der Makrozustände herauszufinden, die am besten nach dem PCCA + -Algorithmus⁵⁰ in MSMbuilder passen, indem Sie das Python-Skript in Supplementary File 1 Python msm_lumping_usingPCCAplus.py verwenden. Identifizieren Sie ein reduziertes kinetisches Netzwerk von Modellen für die wichtigsten Konformationsänderungen von Biomolekülen, indem Sie eine kleine Anzahl von Makrozuständen konstruieren, d.h. Hunderte von Mikrozuständen kinetisch in einen Topf werfen, wie unter^17,51 beschrieben.
   2. Abbildung der hochdimensionalen Konformationen auf das X (Proteinbewegung entlang der DNA-Langachse) und den Rotationswinkel des Proteins entlang der DNA für jeden Makrozustand, wie in Schritt 1.1.3 und 1.1.4 beschrieben (z. B. kein Zustand mit zu niedriger Population < 1%; siehe Abbildung 2C). Suchen Sie dann die 3 Makrozustände, die das System am besten darstellen (Abbildung 1E). In Abbildung 2D finden Sie Momentaufnahmen der Bewegung des Proteins entlang der DNA und des Proteinrotationswinkels um die DNA.
      HINWEIS: In früheren Arbeiten, die den spontanen 10-μs-Protein-Vorwärtsschrittpfad erzeugten, führten wir zusätzlich 5 x 4 μs Gleichgewichts-MD-Simulationen durch, um die Probenahmen moderat zu erweitern. Wir zeigten die Abbildung des ursprünglichen Vorwärtspfades (siehe Abbildung 2A links) und weitere 4-μs-Abtasttrajektorien auf dem zuvor durchgeführten Vorwärtspfad (siehe Abbildung 2A rechts)⁸. Die Abbildung der ursprünglichen 100 × 50 ns (siehe Abbildung 2B links)⁸ und die in dieser Arbeit verwendeten Trajektorien von 97 × 50 ns sind dargestellt (siehe Abbildung 2B rechts).
7. Berechnung der mittleren ersten Durchgangszeiten (MFPT)
   1. Führen Sie fünf 10-ms-Monte-Carlo-Trajektorien (MC) basierend auf dem TPM des 500-Mikrozustands-MSM durch, wobei die Verzögerungszeit von 10 ns als Zeitschritt von MC festgelegt ist. Berechnen Sie MFPT⁵² zwischen jedem Makrozustandspaar (Abbildung 3) mit dem Python-Skript in Supplementary File 1 python python mfpt_msm3.py.
   2. Berechnen Sie den durchschnittlichen und Standardfehler des MFPT mithilfe der bash-Datei in Supplementary File 2, geben Sie Folgendes ein:
      sh mfpt_analysis.bash

2. Durchführung einer grobkörnigen (CG) Simulation zur Abtastung der Langzeitdynamik

1. Führen Sie CG-Simulationen mit der CafeMol 3.0-Software³⁰ durch. Sehen Sie sich die CG-Simulationseinstellungen an, die in der Eingabekonfigurationsdatei mit der Erweiterung .inp angegeben sind, einschließlich Eingabestrukturen, Simulationsparametern, Ausgabedateien usw. Geben Sie den folgenden Befehl auf dem Terminal ein, um die CG-Simulation auszuführen:
   cafemol XXX.inp
2. Geben Sie die folgenden Blöcke in der Eingabedatei an, wobei jeder Block mit der Bezeichnung < and ending with >>>> beginnt.
   1. Legen Sie den Dateinamenblock (erforderlich) fest, um die Arbeitsverzeichnisse und den Speicherpfad der Eingabe-/Ausgabedatei anzugeben. Geben Sie für den Dateinamenblock für diese Simulationen Folgendes ein:
      <<<< Dateinamen
      Pfad = XXXXX (Arbeitspfad)
      filename = wrky (die Namen der Ausgabedateien)
      AUSGABE psf pdb movie dcd rst
      path_pdb = XXXXX (nativer Strukturpfad eingeben)
      path_ini = XXXXX (Eingangsstrukturpfad)
      path_natinfo = XXXXX (nativer Informationsdateipfad)
      path_para = XXXXX (Parameterdateipfad)
      >>>>
      HINWEIS: Da das Go-Modell⁵³ in der CG-Modellierung verwendet wird, d.h. Protein wird auf die native Konformation ausgerichtet, so dass man die modellierte Struktur als native Konformation festlegen muss. Hier wurde die Eingangskristallstruktur als native Konformation festgelegt.
   2. Legen Sie den Jobsteuerungsblock (erforderlich) fest, um die Ablaufweise der Simulationen zu definieren. Geben Sie den folgenden Befehl ein:
      <<<< job_cntl
      i_run_mode = 2 (= 2 die Konstanttemperatursimulation)
      i_simulate_type = 1 (=1 Langevin-Dynamik)
      i_initial_state = 2 (=2 bedeutet, dass die Erstkonfiguration eine native Konfiguration ist)
      >>>>
      Wählen Sie die Simulationen der Langevin-Dynamik mit konstanter Temperatur.
   3. Legen Sie die Einheit und den Statusblock (erforderlich) fest, um die Informationen für Eingabestrukturen zu definieren. Geben Sie den folgenden Befehl ein:
      <<<< unit_and_state
      i_seq_read_style = 1 (=1 bedeutet Lesesequenzen aus der PDB-Datei)
      i_go_native_read_style = 1 (=1 bedeutet, dass die native Struktur aus der PDB-Datei stammt)
      1 Proteinprotein.pdb (Unit & State molecular_type native_structure)
      2-3 DNA-DNA.pdb (unit&state molecular_type native_structure)
      >>>>
      HINWEIS: Die anfänglichen Eingabestrukturdateien (Protein.pdb und DNA.pdb hier) werden benötigt. Die Strukturen sind im PDB-Format geschrieben. Hier werden zwei PDB-Dateien benötigt: eine ist die Proteinstrukturdatei, die die schweren Atomkoordinaten von WRKY (Einheit 1) enthält, und die andere sind die Koordinaten der 200-bp doppelsträngigen (ds) DNA (Einheit 2-3). Das Protein wird zunächst 15 Å von der DNA entfernt platziert.
   4. Setzen Sie den im energy_function Block definierten Energie-Funktionsbaustein (erforderlich). Geben Sie den folgenden Befehl ein:
      <<<< energy_function
      LOKAL(1) L_GO
      LOKAL(2-3) L_DNA2
      NLOCAL(1/1) GO EXV ELE
      NLOCAL(2-3/2-3) ELE-DNA
      NLOCAL(1/2-3) EXV ELE
      i_use_atom_protein = 0
      i_use_atom_dna = 0
      i_para_from_ninfo = 1
      i_triple_angle_term = 2
      >>>>
      HINWEIS: In den CG-Simulationen wird das Protein durch das Go-Modell⁵³ grobkörnig gekörnt, wobei jede Aminosäure durch ein CG-Partikel an seiner Cα-Position dargestellt wird. Die Proteinkonformation wird dann unter dem Go-Potential in Richtung der nativen Struktur oder Kristallstruktur verzerrt (Abbildung 4A links). Die DNA wird durch das 3SPN.2-Modell⁵⁴ beschrieben, in dem jedes Nukleotid durch 3 CG-Partikel S, P, N dargestellt wird, die Zucker, Phosphat bzw. stickstoffhaltiger Base entsprechen (Abbildung 4A rechts). Die elektrostatischen und vdW-Wechselwirkungen werden zwischen verschiedenen Ketten betrachtet. Die elektrostatischen Wechselwirkungen zwischen Protein und DNA in der CG-Simulation werden durch das Debye-Hückel-Potential⁵⁵ angenähert. Die vdW-Abstoßungsenergie nimmt die gleiche Form an wie beim Go-Modell.
   5. Setzen Sie den md_information Block (erforderlich), um die Simulationsinformationen zu definieren. Geben Sie den folgenden Befehl ein:
      <<<< md_information
      n_step_sim = 1
      n_tstep(1) = 500000000
      tstep_size = 0,1
      n_step_save = 1000
      n_step_neighbor = 100
      i_com_zeroing = 0
      i_no_trans_rot = 0
      tempk = 300,0
      n_seed = -1
      >>>>
      Der n_tstep ist der Simulationsschritt. Legen Sie die tstep_size als Zeitlänge jedes MD-Schritts fest, jeder CG Cafemol-Zeitschritt beträgt etwa 200 fs³⁰, so dass jeder MD-Schritt hier im Prinzip 200 × 0,1 fs beträgt. Aktualisieren Sie die Nachbarliste alle 100 MD-Schritte (n_step_neighbor = 100). Stellen Sie die Simulationstemperatur auf 300 K ein. Steuern Sie die Temperatur, indem Sie den geschwindigkeitsartigen Verlet-Algorithmus zur Aktualisierung der Proteinstruktur mit dem Berendsen-Thermostat⁵⁶ verwenden.
      HINWEIS: Die n_step_sim ist die Beckennummer des auf dem Go-Modell basierenden Potentials oder die lokale Minimalzahl der Energiekurve. Ein Multi-Basin-Potential ermöglicht es, dass die Proteinkonformation auf verschiedene Konformationen verzerrt ist, so dass sich die Proteinkonformation von einem lokalen Minimum zum anderen ändern kann. Hier wird nur das Einzelbecken-Go-Modell verwendet, was in den Simulationen nur eine verzerrte Konformation (Kristallstruktur) für Protein bedeutet. Da im CG-Kontext keine Protein-DNA-Wasserstoffbrückenbindungsinteraktion usw. modelliert ist, können die molekularen Bewegungen noch schneller, d.h. > 10-mal als in den atomaren Simulationen, abgetastet werden.
   6. Setzen Sie den elektrostatischen Block (nur erforderlich, wenn elektrostatische Wechselwirkungen verwendet werden), da die elektrostatische Wechselwirkung zwischen verschiedenen Ketten betrachtet wird, also verwenden Sie diesen Block, um die Parameter für die elektrostatische Wechselwirkung zu definieren, indem Sie Folgendes eingeben:
      <<<< elektrostatisch
      cutoff_ele = 10,0
      ionic_strength = 0,15
      >>>>
      Setzen Sie die Debye-Länge in der elektrostatischen Wechselwirkung auf 10 Å, entsprechend der Lösungsbedingung. Stellen Sie die Ionenstärke auf 0,15 M ein, wie bei der physiologischen Bedingung.

Ergebnisse

Rotationsgekoppeltes Gleiten oder 1 bp Treten von WRKY aus der MSM-Konstruktion
Alle Proteinkonformationen auf der DNA werden auf die Längsbewegung X und den Rotationswinkel des Proteins COM entlang der DNA abgebildet (siehe Abbildung 3A). Die lineare Kopplung dieser beiden Grade zeigt ein rotationsgekoppeltes Stepping des WRKY-Domänenproteins auf der DNA an. Die Konformationen können im MSM weiter in 3 Makrozustände (S1, S2 und S3) gruppiert werden. Das Vorwärtsstep...

Diskussion

Diese Arbeit befasst sich mit der Durchführung strukturbasierter Computersimulationen und Probenahmen, um einen Transkriptionsfaktor oder ein TF-Protein aufzudecken, das sich entlang der DNA bewegt, nicht nur im atomaren Detail des Steppens, sondern auch in der prozessiven Diffusion, die für die erleichterte Diffusion von TF in der DNA-Zielsuche unerlässlich ist. Dazu wurde zunächst das Markov-Zustandsmodell oder MSM eines kleinen TF-Domänenproteins WRKY konstruiert, das für 1-bp entlang homogener Poly-A-DNA schrit...

Materialien

Name	Company	Catalog Number	Comments
CafeMol	Kyoto University		coarse-grained (CG) simulations
GROMACS	University of Groningen Royal Institute of Technology Uppsala University		molecular dynamics simulations software
Matlab	MathWorks		Numerical calculation software
MSMbuilder	Stanford University		build MSM
VMD	UNIVERSITY OF ILLINOIS AT URBANA-CHAMPAIGN		molecular visualization program