Cuantitativa de la dureza de medición por instrumentado AFM-muesca

Resumen

This experimental protocol describes how atomic force microscopy can be used to measure hardness at the true nanometer scale and to detect single atomistic plasticity events.

Resumen

In this work, a combination of amplitude-modulated non-contact atomic force microscopy and atomic force spectroscopy is applied for instrumented hardness measurements on an Au(111) surface with atomistic resolution of single plasticity events. A careful experimental procedure is described that includes the force sensor selection, its calibration, the calibration of the cantilever deflection detection system, and the minimization of instrumental drift for accurate and reproducible force-distance measurements. Also, a method for the data analysis is presented that allows the extraction of force-penetration curves from recorded force-distance curves. A typical curve displays a clear elastic deformation regime up to the first plasticity event, or pop-in, with a length in the range of one to two Burger's vectors. Later plasticity events exhibit the same magnitude. The work of plasticity is further extracted from the measurements. Finally, the hardness is determined in combination with the indentation curve using non-contact atomic force microscopy images of the remaining indents.

Introducción

For the last 150 years, hardness values have been used to characterize the mechanical behavior of materials and to predict their performance under various loading conditions. The hardness of a material describes the resistance of its surface to the penetration of a harder indenter. For metallic materials, the hardness relates to resistance to plastic flow.

Although the implementation of hardness testing has proven to be relatively easy, the yielded results have long been rather empirical, making them unable to describe the intrinsic properties of the investigated material. The empirical nature of hardness testing results has been a consequence of the use of various indenter geometries, each of which has a different established hardness scale. However, all empirical hardness scales, such as the Brinell hardness (HB) test for spherical indenters and the Vickers (HV) and Knoop (HK) hardness tests for different types of four-sided pyramids, have one thing in common: the hardness number is determined from the ratio of the applied load to the developed area of the remaining indent. In an attempt to relate the hardness of metals to their fundamental mechanical properties, the hardness measured with a spherical indenter has been defined as the ratio of the applied load to the projected area of the remaining indent. This hardness value, also known as the Meyer's hardness (H), is equal to the mean contact pressure and directly relates to the yield strength of non-work-hardening metals¹.

Hardness testing has long been limited to the macro-scale, in which case the sizes of indents have been measured by optical means. The development of instrumented indentation, where force-displacement curves are recorded, has been recognized as a valuable alternative for determining the hardness of a material, although the size of the remaining indent may be too small to be accurately imaged. In this case, the projected area of the indent is calculated from the tip displacement according to a so-called indenter-area function². Due to this development, the analysis of the curvature of force-displacement curves and of the occurrence of distinct plasticity events in the shape of pop-ins is now widely used to study the mechanisms of plastic deformation at the micrometer scale, such as by means of nanoindentation³.

It is well accepted that the carriers of plastic deformation in metals, i.e., dislocations, operate at the nanometer scale. To understand their modes of operation at the atomic level, new experimental techniques with atomic resolution are needed. Initial investigations of atomistic plasticity events at the interfaces between nanometer-sized single asperities and single crystalline Au surfaces of different orientations have been carried out by interfacial force microscopy (IFM)^{4, 5}. Atomic force microscopy (AFM) indentation has been applied to observe the nucleation and gliding of single dislocations in KBr(100) single crystals⁶, Cu(100)⁷, and Au(111)^{8, 9}. There, atomistic plasticity events were observed in the shape of pop-ins, with lengths in the range of 1 Å. AFM indentation has also been used to measure the nano-hardness and -elasticity of gold nano-island grown on mica¹⁰. In this work, the nano-hardness was found to be smaller than the bulk value and was observed to depend linearly on the indentation area. Also, a detailed measurement protocol has been proposed to determine the hardness of hard surfaces, such as fused quartz and silicon, by AFM indentation with a diamond-tipped sapphire cantilever¹¹. In particular, this method takes into account the non-linearity of the photo-sensitive deflection detectors for large cantilever deflection¹². More recently, AFM indentation and non-contact AFM imaging have been combined to quantitatively determine the hardness and the fundamental mechanisms of plastic deformation of a Pt(111) single crystalline surface and Pt-based metallic glass¹³. For Pt(111), plastic deformation mechanisms at the nanometer scale were found to be consistent with the discrete mechanisms established for larger scales. Further, the nanometer-scale plastic deformation of the metallic glass was found to be not discrete, but rather continuous and highly localized around the indenting tip. These results revealed a lower size limit for metallic glasses, below which shear transformation mechanisms are not activated by indentation. AFM indentation has also been used to determine the hardness values of biological samples (such as collagen fibrils)¹⁴, polymers¹⁵, and colloidal crystals¹⁶.

In the present work, a careful experimental procedure is described that includes the force sensor selection, its calibration, the calibration of the cantilever deflection detection system, and the minimization of instrumental drift for accurate and reproducible force-distance measurements. Also, a method for the data analysis is presented that allows the extraction of force-penetration curves from recorded force-distance curves. Further representative results are shown and discussed in the light of recent findings in the field of plastic deformation of small volumes.

For this experiment, an atomic force microscope (AFM) was used. The cornerstone of an AFM is its micro-fabricated force sensor (usually a cantilever beam), with a sharp tip at the end whose radius is in the range of several nanometers. In the particular configuration of the instrument used for this experiment, the cantilever is mounted onto a piezo-electric z-scanner, while the sample to be investigated is mounted onto a piezo-electric x/y-scanner. During AFM imaging, the force sensor tip is scanned over a sample to register interaction forces with the sample surface that result in a deflection of the cantilever according to Hooke's law. The static or dynamic deflection of the cantilever can be measured with an optical beam deflection detector, consisting of a laser diode, a set of mirrors, and a photodiode that converts the cantilever deflection into a voltage. During imaging, the signal at the photodiode is controlled by a feedback loop so as to keep the interaction forces at the sample surface; this results in adjustments of the z-scanner position, which are recorded and displayed as a topography image.

Prerequisites for the experiment described below are that the piezo-electric scanners of the atomic force microscope are well-calibrated and that the instrument stays in the laboratory at a constant temperature and humidity level. The reader should be aware that, depending on the atomic force microscope model, some of the experimental procedure steps may have to be modified. In particular, all measurements are performed after setting the scanners' ranges to "small"; this function allows for the reduction of the x/y-scanner range to 5 x 5 µm² and the z-scanner range to 4 µm, which ensures a resolution at small scales. This function is not available on all commercial AFM and is not mentioned in the remainder of the text.

For data analysis, the use of the free SPM data analysis software Gwyddion¹⁷ and the Matlab software package¹⁸ are recommended.

This protocol gives a description of the experimental procedure to be followed in order to perform instrumented hardness measurements by AFM. Since the handling of different commercial AFMs may differ from one model to the other, the reader should refer to the manual provided by the AFM manufacturer for detailed setting procedures and software information. In the following text, in order to reproduce the described experiment, it is assumed that the reader is familiar with the handling of the particular AFM used here.

Protocolo

1. Conjunto Instrumental en marcha y calibración

1. Instrumental puesta a punto
   1. Use un voladizo rígido con recubrimiento de diamante del tipo DT-NCLR o CDT-NCLR con una primera frecuencia de resonancia f libre _0,1 ≥ 180 kHz, un factor de calidad Q ≥ 300, y una rigidez a la flexión k ≥ 40 N / m.
   2. Montar el voladizo seleccionado en un soporte de sujeción proporcionado por el fabricante AFM. Tenga especial cuidado para colocar el voladizo de tal manera que su eje longitudinal es perpendicular a la dirección de exploración rápida de la AFM. Alternativamente, pegar el voladizo en un soporte en voladizo proporcionado por el fabricante AFM con pegamento epoxi de dos componentes.
   3. Montar el soporte en voladizo sobre la cabeza AFM y utilizar el microscopio óptico normalmente disponible con el sistema de AFM para centrarse en el voladizo del AFM. a comprobar que el eje largo del voladizo es perpendicular a la dirección de exploración rápida. Si no, volver aSección 1.1.2.
   4. Alinear el haz láser de modo que se refleja en el extremo del voladizo. Monitorear la suma de tensión en el fotodiodo y llevar a cabo un ajuste fino para maximizar la señal suma. valores de señal de suma típicas están en el intervalo de 2 V.
   5. Ajustar ángulos de inclinación horizontal y vertical del espejo con el fin de llevar el punto de láser se refleja en el centro de la fotodiodo, donde las tensiones correspondientes al desplazamiento vertical y lateral son casi cero.
2. Calibración
   1. Realizar un barrido de frecuencias para determinar la primera resonancia plegado libre f _0,1 del voladizo.
   2. Determinar la rigidez a la flexión del voladizo k, calculado de acuerdo con ¹⁹
      (1)
      donde E es el módulo de Young, L es la longitud del voladizo, w es la anchura de la cantilnunca, y t es su espesor. Con este fin, medir la longitud y la anchura del voladizo por microscopía óptica o microscopía electrónica de barrido para una mayor precisión. Calcular el espesor del voladizo desde su primera frecuencia de resonancia de flexión libre f _0,1, de acuerdo con
      (2)
      donde ρ es la densidad de masa.
   3. Seleccione el valor predeterminado de la sensibilidad fotodiodo para el tipo voladizo particular a ser utilizado para el experimento en el menú de configuración de la AFM. Llevar la punta en voladizo en contacto con la muestra de referencia en una carga F _n = 10 nN haciendo clic en el botón de enfoque.
   4. Abrir el menú de la espectroscopia de fuerza en el software de AFM y establecer la retracción relativa y extensión de la z-scanner a 50 nm y la z-scanner retracción / extensión a 0,3 m / seg. Si lo hace, el registro de la curva de fuerza-distancia seconsistir primero de una retracción de la z-scanner a 50 nm de distancia de la superficie de la muestra y después de una serie de enfoques y retracciones de la misma distancia.
   5. Registrar una curva de distancia de la fuerza con los parámetros establecidos en 1.2.4 sugeridas sobre una superficie lisa y no conforme, como diamantes nano-cristalino o zafiro, con el fin de evitar los efectos de deformación de la muestra. Para ello haga clic en el botón adquirir en el menú de espectroscopia de fuerza del software AFM.
   6. Montar la parte repulsiva de la curva de fuerza-distancia con una función lineal, en el menú de calibración del software AFM. La pendiente inversa de la línea de montaje corresponde a la sensibilidad S fotodiodo. Sustituir el valor determinado con el valor por defecto del software del instrumento en el menú de calibración del software AFM haciendo clic en el botón de ejecución de calibración.

Preparación 2. Muestra

NOTA: La muestra se mide en this experimento consiste en un 100-nm de espesor de película delgada, lisa atómicamente Au (111) crecido sobre mica por deposición física de vapor.

1. Montar la muestra en un soporte de muestras magnético proporcionado por el fabricante del instrumento por medio de cinta de doble cara de carbono. Con el fin de evitar la deriva de la muestra durante las mediciones, montar la muestra de un día antes de las mediciones, a fin de permitir que la cinta de carbono relajarse. Alternativamente, montar la muestra en el soporte con la pintura de plata, que generalmente se seca en pocos minutos.
2. Montar el soporte de la muestra magnética en el x / y escáner.

3. Procedimiento de medición

1. Establecer la frecuencia de oscilación ligeramente fuera de resonancia (en este experimento f = 190.67 kHz) y la amplitud de oscilación en A = 20 nm Tenga en cuenta que estos valores se establecen de forma automática por el software del instrumento para este voladizo en particular. Ajuste el punto de ajuste de oscilación de forma manual en _{un punto} de _referencia = 5 nm.
2. Dibujarel voladizo hacia la superficie de la muestra utilizando el motor paso a paso de la AFM. Asegúrese de que el sensor de fuerza no choquen con la superficie de la muestra. Mantenga el foco en voladizo durante la aproximación gruesa y detener el enfoque gruesa antes de la superficie de la muestra con un enfoque perfecto.
3. Abordar de forma automática el sensor de fuerza haciendo clic en el botón de enfoque. Una vez que la amplitud de oscilación ha llegado a su punto de ajuste, la punta está listo para escanear la topografía de la superficie de la muestra.
4. Grabar una serie de imágenes de la topografía en áreas que van desde 5 x 5 a 1 x 1 μm² (si está disponible, ajustar la pendiente de la señal de la topografía por la inclinación del X / Y-escáner). Asegúrese de que las imágenes sucesivas de la misma zona, que no presentan ningún signo de la deriva y que la posición z-escáner permanece casi constante. Si este no es el caso, continúe formación de imágenes hasta que el sistema se haya estabilizado.
5. Una vez que el sistema se haya estabilizado y un suave 1 x 1 μm² zona se ha encontrado, retraer el force sensor de unos pocos micrómetros de la superficie de la muestra haciendo clic en el botón de retracción.
6. Seleccione el modo de la espectroscopia de fuerza en el menú del instrumento y mover el sensor de fuerza para el medio de la zona preseleccionada μm² 1 x 1, con una fuerza de punto de referencia de 10 nm. Controlar la posición de la z-escáner hasta que se mantiene constante.
7. Seleccione la cuadrícula 2 x 2 de puntos cuyo centro corresponde al centro de la zona preseleccionada μm² 1 x 1. Establecer la distancia entre dos puntos vecinos próximos a 500 nm.
8. Ajustar la distancia del escáner con respecto a variar de 0 a 150 nm a una velocidad de 300 nm / s, y a continuación retraer en la misma distancia y a la misma velocidad. Teniendo en cuenta el ángulo de inclinación del voladizo con respecto a la superficie de la muestra, aplicar una corrección de la inclinación moviendo el escáner lateral por Z × tan φ durante una extensión de escáner vertical Z, donde φ es el ángulo de inclinación ^20.
   NOTA: Algunos instruments representan la inclinación en voladizo en su espectroscopia de fuerza o modo de sangrado; este es el caso para el AFM utilizada en este trabajo.
9. Presione el botón de inicio en el software del instrumento para iniciar la adquisición de los datos de AFM de sangría.
10. Una vez que se han completado las mediciones de AFM de sangría, retraer el sensor de fuerza unos pocos micrómetros de distancia de la superficie de la muestra.
11. Seleccione la imagen sin contacto modo de AFM en el menú de software del instrumento y repita el procedimiento descrito en las secciones 3.1 y 3.2.
12. Realizar un análisis sobre el mismo 1 x 1 μm² superficie como en la sección 3.3 con el fin de localizar la posición exacta de los guiones. Más escanea la superficie más de un área de superficie nm² 500 x 500 se pueden realizar para la imagen de los guiones restantes con mayor detalle.

Análisis 4. Datos

1. Procesamiento de imágenes
   1. Procesar las imágenes grabadas topografía fin de alinear las líneas en el directorio de exploración rápidaexión basada en la diferencia media. Utilice la función incorporada de Gwyddion.
2. Calcular el área proyectada A _p de guiones utilizando la función de análisis sangría de Gwyddion.
3. Estimar la forma de la punta del AFM de las imágenes de la topografía de guiones mediante el uso de la función de análisis punta de Gwyddion. A continuación, un promedio de las imágenes de forma de punta y medir el ángulo de apertura de la mitad α de la forma de la punta promediado.
4. Convertir las curvas de fuerza-distancia en las curvas de fuerza-desplazamiento mediante el cálculo del desplazamiento de la punta δ acuerdo con ¹³
   (3)
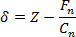
   donde Z es la posición del escáner relativa.
5. Ahora, trazar la fuerza en función del desplazamiento de la punta. La curva resultante muestra generalmente llamados pop-ins, con longitudes del orden de varios 100 horas, que corresponden a eventos de plasticidad atomizados. Utilizar el primero de los these pop-ins para determinar el desplazamiento de la punta en el límite elástico δ _el ^4.
6. Montar la parte elástica de la curva de fuerza-desplazamiento con la función de Hertz ^21.
   (4)
   donde R es el radio de la punta y E ^'* es la reducción del módulo de elasticidad, dada por , Con M _s, siendo _t el módulo de muesca de la muestra y de la punta, respectivamente. En este caso, el parámetro de ajuste es .
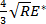7. Extender la función de ajuste en el régimen de la plasticidad así como para calcular el trabajo de la plasticidad W _plasticidad de la diferencia de área entre la función de ajuste y la curva experimental ^21.
8. Calcular la dureza de la muestra de acuerdo con ^{1, 2}
   (5)
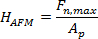
   y
   (6)
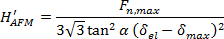
   donde F _{n, max} es la carga máxima aplicada, _Ap es el área proyectada del guión calculado en la Sección 4.2, α es el ángulo de apertura de la mitad de la punta calculada en la Sección 4.3, δ _EL es el desplazamiento de la punta en la primera plasticidad evento, y δ es el _máximo desplazamiento de la punta máxima (ver sección 4.4).

Resultados

En este trabajo, la rigidez a la flexión del voladizo k se calcula de acuerdo con la teoría de la viga ¹⁹ geométrica. Para el cantilever con recubrimiento de diamante particular utilizado en este trabajo, encontramos k = 55,69 N / m. Tenga en cuenta que hemos descuidado el revestimiento de diamante; el espesor de la capa de diamante es de uno a dos órdenes de magnitud menor que el espesor en voladizo y por lo tanto no aumenta de manera significativa su re...

Discusión

Un método ha sido presentado para la realización de una serie de muescas en Au (111) de superficie de película delgada con una punta de AFM con recubrimiento de diamante. Sin contacto AFM de imágenes y la sangría AFM se realizaron con el mismo sensor de fuerza. Los requisitos para la formación de imágenes sin contacto son una gran primera frecuencia de resonancia f libre de _0,1 ≥ 180 kHz y un alto factor de calidad Q ≥ 300. En AFM sangría, la fuerza vertical que se aplic...

Materiales

Name	Company	Catalog Number	Comments
AFM XE-100	Park Instruments	discontinued	Atomic force microscope
CDT-NCLR	NanoSensors	CDT-NCLR	Conductive diamond coated non-contact lever
100 nm thick Au(111) thin film on Mica	Phasis	20020011	atomically smooth gold thin film