Determinación de la resistencia mecánica de metales de grano ultrafino

Resumen

El protocolo presentado aquí describe los experimentos radiales de alta presión diamante-yunque-célula y analiza los datos relacionados, que son esenciales para obtener la resistencia mecánica de los nanomateriales con un avance significativo en el enfoque tradicional.

Resumen

El fortalecimiento mecánico de los metales es el desafío de larga data y el tema popular de la ciencia de los materiales en las industrias y la academia. La dependencia del tamaño de la fuerza de los nanometales ha atraído mucho interés. Sin embargo, caracterizar la resistencia de los materiales a menor escala nanométrica ha sido un gran desafío porque las técnicas tradicionales ya no son efectivas y confiables, como la nanoindentación, la compresión micropilar, la tracción, etc. El protocolo actual emplea técnicas de difracción de rayos X (XRD) de células radiales de diamante-yunque (rDAC) para rastrear los cambios de tensión diferencial y determinar la resistencia de los metales ultrafinos. Se encuentra que las partículas de níquel ultrafinas tienen un límite elástico más significativo que las partículas más gruesas, y el fortalecimiento del tamaño del níquel continúa hasta 3 nm. Este hallazgo vital depende enormemente de técnicas de caracterización efectivas y confiables. Se espera que el método rDAC XRD desempeñe un papel importante en el estudio y la exploración de la mecánica de nanomateriales.

Introducción

La resistencia a la deformación plástica determina la resistencia de los materiales. La resistencia de los metales generalmente aumenta con la disminución del tamaño del grano. Este fenómeno de fortalecimiento del tamaño puede ser bien ilustrado por la teoría tradicional de la relación Hall-Petch desde el milímetro hasta el régimen^{submicrométrico 1,2}, que se basa en el mecanismo de deformación mediado por dislocación de metales de tamaño a granel, es decir, dislocaciones se acumulan en los límites de grano (GB) y dificultan sus movimientos, lo que lleva al fortalecimiento mecánico en metales ^3,4.

En contraste, el ablandamiento mecánico, a menudo conocido como la relación inversa Hall-Petch, se ha reportado para nanometales finos en las últimas dos décadas 5,6,7,8,9,10. Por lo tanto, la resistencia de los nanometales sigue siendo desconcertante, ya que se detectó un endurecimiento continuo para tamaños de grano de hasta ~ 10 nm^11,12, mientras que los casos de ablandamiento de tamaño por debajo del régimen de 10 nm también se informaron ^7,8,9,10. La principal dificultad o desafío para este tema debatido es hacer mediciones estadísticamente reproducibles sobre las propiedades mecánicas de los nanometales ultrafinos y establecer una correlación confiable entre la fuerza y el tamaño de grano de los nanometales. Otra parte de la dificultad proviene de la ambigüedad en los mecanismos de deformación plástica de los nanometales. Se han reportado varios defectos o procesos a nanoescala, incluyendo dislocaciones^13,14, hermanamiento de deformación 15,16,17, fallas de apilamiento ^15,18, migración gb¹⁹, deslizamiento GB 5,6,20,21, rotación de grano 22,23,24, parámetros de enlace atómico 25,26,27,28, etc. Sin embargo, aún no está claro cuál domina la deformación plástica y, por lo tanto, determina la resistencia de los nanometales.

Para estos problemas anteriores, los enfoques tradicionales de examen de resistencia mecánica, como la prueba de tracción²⁹, la prueba de dureza vickers ^30,31, la prueba de nanoindentación³², la compresión micropilar ^33,34,35, etc. son menos efectivos porque la alta calidad de grandes piezas de materiales nanoestructurados es muy difícil de fabricar y el indentador convencional es mucho más grande que una sola nanopartícula de materiales (para el mecánica de una sola partícula). En este estudio, introducimos las técnicas radiales DAC XRD 36,37,38 a la ciencia de materiales para rastrear in situ el texturizado de tensión de rendimiento y deformación de nano níquel de varios tamaños de grano, que se utilizan en el campo de la geociencia en estudios anteriores. Se ha encontrado que el fortalecimiento mecánico se puede extender hasta 3 nm, mucho más pequeño que los tamaños más sustanciales de nanometales reportados anteriormente, lo que amplía el régimen de la relación convencional Hall-Petch, lo que implica la importancia de las técnicas rDAC XRD para la ciencia de materiales.

Protocolo

1. Preparación de la muestra

1. Obtener polvo de níquel de 3 nm, 20 nm, 40 nm, 70 nm, 100 nm, 200 nm y 500 nm de fuentes comerciales (consulte la Tabla de materiales). La caracterización morfológica se muestra en la Figura 1.
2. Prepare partículas de níquel de 8 nm calentando partículas de níquel de 3 nm utilizando un hervidor de reacción (consulte la Tabla de materiales).
   1. Ponga ~ 20 ml de etanol absoluto y ~ 50 mg de polvo de níquel de 3 nm en el hervidor de reacción. NOTA: La solución completa no debe alcanzar ~ 70% del volumen de la tetera.
   2. Calentar el hervidor de reacción a 80 °C durante 24 h.
   3. Enfríe la solución a temperatura ambiente y deje caer una pequeña solución a una malla de cobre (rejilla TEM, consulte la Tabla de materiales).
   4. Coloque la malla de cobre seco en la cámara de microscopía electrónica de transmisión (TEM) y observe la morfología de la muestra bajo un haz de electrones de voltaje de 200 kV.
      NOTA: La malla de cobre se secó al aire durante ~ 5 minutos o se usó una luz de secado de 5 minutos.
   5. Mida manualmente la distribución del tamaño de partícula a partir de las imágenes TEM.
      NOTA: La medición del tamaño de partícula también se puede realizar utilizando cualquier software disponible gratuitamente, como Image J.
   6. Saque la solución y vaporize el etanol a temperatura ambiente; luego, el resto del sólido negro es el polvo de níquel puro con un tamaño de partícula promedio de 8 nm.
3. Preparar polvo de níquel de 12 nm
   1. Repita el paso 1.2, pero cambie el "etanol absoluto" y "80 °C durante 24 h" a "isopropanol absoluto" y "150 °C durante 12 h" para obtener el polvo de níquel puro con la partícula promedio de 12 nm.

2. Mediciones radiales DAC XRD de alta presión

1. Haga una junta de boro-epoxi transparente de rayos X utilizando una máquina de perforación láser (consulte la Tabla de materiales).
   1. Preparar kapton (una especie de plástico) juntas de soporte
      NOTA: Kapton es un material de película de poliimida (ver Tabla de Materiales).
      1. Corte el círculo interior con una máquina perforadora láser utilizando los parámetros mencionados: 35% de potencia láser, tres pasadas, 0,4 mm / s (velocidad de corte).
      2. Cortar el rectangular exterior utilizando los parámetros: 80% de potencia láser, dos pasadas, 1,2 mm/s (velocidad de corte). La dimensión rectangular es de 8 x 1,4 mm.
   2. Prepare juntas de boro-epoxi a partir de un disco de boro más grande con un diámetro de ~ 10 mm.
      NOTA: El disco de boro se hace comprimiendo la mezcla de polvo de boro amorfo y pegamento epoxi³⁶.
      1. Pulir los discos crudos a un grosor de 60-100 μm con papel de lija manualmente.
         NOTA: El papel de lija es de ~ 400 malla a ~ 1000 malla.
      2. Corte los círculos internos con una máquina perforadora láser utilizando los parámetros mencionados: 35% de potencia láser, tres pasadas, 0.4 mm / s (velocidad de corte).
      3. Corte el círculo exterior con una máquina perforadora láser: 30% de la potencia del láser, una pasada, 0,4 mm / s (velocidad de corte). Repita y deténgase inmediatamente cuando se desprenda.
   3. Montar las juntas
      1. Coloque una junta de soporte Kapton (preparada en el paso 2.1.1) en un portaobjetos de vidrio.
      2. Coloque una junta de boro perforada en el orificio interior de la junta Kapton. Asegúrese de que el extremo más grande de la junta de boro esté en la parte superior.
      3. Coloque otro portaobjetos de vidrio limpio en la parte superior. Sosténgalo firmemente y presiónelo hasta que la junta se inserte firmemente en el orificio de la junta Kapton.
      4. Guarde los conjuntos de juntas fabricados entre dos portaobjetos de vidrio limpio y envuélvalos con cinta adhesiva para su uso futuro.
         NOTA: El diámetro de la junta, Ø = tamaño del culet de diamante + 150 μm. Para una mejor reproducibilidad, se pueden usar las mismas configuraciones (posiblemente con pequeños ajustes si se encuentra algo mal) para la perforación y el corte por láser durante la preparación de la junta. Para una buena coincidencia de tamaño, el diámetro de las juntas introducidas para el corte por láser es Ø + 23 μm, mientras que el diámetro del orificio interior de las juntas de soporte Kapton (ingresado para el corte por láser) es Ø - 23 μm.
2. Carga del experimento DAC radial
   1. Monte el conjunto de la junta
      1. En el monitor de la computadora de visualización (conectado al microscopio óptico), marque un punto para ubicar el centro del diamante (el diamante del pistón del DAC).
      2. Monte la junta de boro-epoxi (preparada en el paso 2.1) y la marca en el centro del orificio de la junta.
      3. Use una corredera de vidrio para presionar hacia abajo el conjunto de la junta de tal manera que la junta se fije firmemente en el diamante del pistón.
         NOTA: Un DAC tiene dos piezas idénticas de diamantes. Generalmente, el superior se llama diamante de cilindro, y el inferior se llama diamante de pistón.
   2. Limpieza y compactación de la configuración de la junta
      1. Cargue muestras con un tamaño de trozo más pequeño que el orificio de la junta de modo que no haya desbordamiento de materiales en la superficie de la junta.
         NOTA: Las muestras aquí significan los materiales candidatos que estudiamos en nuestros experimentos. En este estudio, las muestras son polvos de Ni de diferentes tamaños y chips de Pt.
      2. Cierre la celda después de la carga de una nueva pieza de muestra para lograr la compacidad.
   3. Carga de materiales blandos (como el oro)
      1. Cargue solo una pieza de la muestra blanda (haga que el material blando sea una pequeña fracción de los materiales cargados).
      2. Use materiales amorfos duros para llenar el orificio de la junta para una buena compacidad.
   4. Carga de materiales de bajo número atómico (como espinela, piropo, serpentina)
      1. Mezclar la muestra con 10% Pt o Au. Llene el orificio de la junta con la mezcla pero sin desbordamiento.
      2. Si es necesario, coloque materiales amorfos duros en la parte superior para una buena compacidad.
3. Estudio de difracción de rayos X
   1. Monte la junta de rayos X transparente de boro-Kapton (preparada en la etapa 2.1) con un espesor de 100 μm y un orificio de cámara de 60 μm en la parte superior del culet de 300 μm de DAC con el soporte de las arcillas.
   2. Coloque un pequeño trozo de chip Pt encima de la muestra de Ni como calibrante de presión.
      NOTA: No se utilizó ningún medio de presión para maximizar la tensión diferencial entre el axial y el radial.
   3. Utilice una radiografía de sincrotrón monocromática (ver Tabla de materiales) con una energía de 25 o 30 keV para realizar los experimentos de difracción de rayos X.
   4. Enfoque el haz de rayos X a ~30 x 30 μm² de superficie en la muestra.
   5. Recopile los patrones de difracción de rayos X a intervalos de presión de 1-2 GPa mediante una placa de imagen de dos dimensiones (consulte la Tabla de materiales) con una resolución de 100 μm/píxel. La configuración utilizada se muestra en la Figura 2 y la Figura 3.
4. El análisis experimental de datos
   1. Procese cada imagen de difracción de rayos X en un archivo que contenga 72 espectros en pasos azimutales de 5° utilizando Fit2d 37,38,39,40,41,42.
      NOTA: Una imagen de difracción bidimensional contiene información de 360°. Para analizar la información de estrés y textura, es necesario separar en 72 archivos con información azimutal de 5° contenida en cada uno. Fit2d es el software utilizado para analizar datos de difracción de rayos X 37,38,39,40,41,42.
   2. Refinar el patrón de difracción con el método Rietveld en el software MAUD³⁷. La tensión de red de cada plano de celosía se obtuvo ajustando el patrón^37,40.
   3. Calcule la tensión diferencial y el límite elástico de acuerdo con la teoría de la deformación de la red³⁸ y el criterio de rendimiento de von Mises ^38,39 siguiendo el paso 2.5.
5. La teoría de la deformación reticular para el análisis experimental de datos
   1. Determinar la tensión diferencial (la diferencia entre estos componentes de tensión máxima (σ₂₂ = σ₃₃) y tensión mínima (σ₁₁)) que proporciona una estimación de límite inferior del límite elástico de un material³⁸, σ_y, basada en el criterio de rendimiento de von Mises siguiendo la ecuación (1)³⁸:
      (1) t= σ_{11-σ 33}<2τ= σ_y.
   2. Obtener la deformación desviatoria dependiente de la dirección Q_hkl midiendo los espaciados d a partir de diferentes direcciones de difracción siguiendo la ecuación (2)³⁸:
      (2)
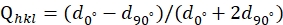
      donde d_0° y d_90° son los espaciados d medidos desde Ψ = 0° y Ψ = 90° (el ángulo entre el vector de difracción y el eje de carga), respectivamente.
   3. Luego, derive el valor de t usando la ecuación (3)³⁸:
      
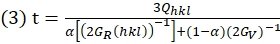
      donde G_R(hkl) y G_v son el módulo de cizallamiento de los agregados bajo la condición de Reuss (iso-tensión) y Voigt (iso-tensión), respectivamente; α es el factor para determinar el peso relativo de las condiciones de Reuss y Voigt⁴⁰.
      NOTA: Teniendo en cuenta las complicadas condiciones de estrés / tensión de los experimentos actuales, se utiliza α = 0.5 en este estudio.
   4. Para un sistema cúbico, calcule G_R(hkl) y G_vde la siguiente manera usando las ecuaciones 4-6 38,40,41:
      (4)
      (5)
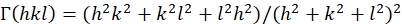
      (6)
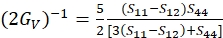
      donde S_ij son los cumplimientos elásticos monocristalinos y se pueden obtener a partir de las constantes de rigidez elástica C_ij de los materiales.

3. Mediciones de TEM

1. Prepare láminas delgadas de Ni presurizadas para TEM utilizando un sistema de haz de iones enfocado (FIB) (consulte la Tabla de materiales). Para reducir los posibles artefactos durante el fresado iónico de la muestra, deposite una capa protectora de Pt utilizando la pistola Pt equipada en el SEM con un grosor de ~ 1 μm en la región candidata.
2. Realice mediciones TEM en un microscopio electrónico de transmisión corregido por aberración de 300 kV equipado con detectores de campo oscuro anular de alto ángulo (HAADF) y campo brillante (BF).
3. Tome imágenes TEM de alta resolución.

Resultados

Bajo compresión hidrostática, las líneas de difracción de rayos X no enrolladas deben ser rectas, no curvas. Sin embargo, bajo presión no hidrostática, la curvatura (elipticidad de los anillos XRD, que se traduce en la no linealidad de las líneas trazadas a lo largo del ángulo azimutal) aumenta significativamente el níquel de grano ultrafino a presiones similares (Figura 4). A una presión similar, la tensión diferencial del níquel de tamaño 3 nm es la más alta. Los resultados d...

Discusión

Las simulaciones computacionales se han empleado ampliamente para estudiar el efecto del tamaño de grano en la fuerza de los nanometales ^{5,6,16,17,27,42}. Se ha propuesto que las dislocaciones perfectas, las dislocaciones parciales y la deformación de GB desempeñan un papel decisivo en los mecanismos de deformación de los ...

Materiales

Name	Company	Catalog Number	Comments
20 nm Ni	Nanomaterialstore	SN1601	Flammable
3 nm Ni	nanoComposix		Flammable
40, 70, 100, 200, 500 nm Ni	US nano	US1120	Flammable
Absolute ethanol			as the solution to make 8 nm Ni
Absolute isopropanol			as the solution to make 12 nm Ni
Amorphous boron powder	alfa asear
Copper mesh	Beijing Zhongjingkeyi Technology Co., Ltd.		TEM grid
Epoxy glue
Ethanol			clean experimental setup
Focused ion beam	FEI
Glass slide
Glue tape	Scotch
Kapton	DuPont		Polyimide film material
Laser drilling machine			located in high pressure lab of ALS
Monochromatic synchrotron X-ray	Beamline 12.2.2, Advanced Light Source (ALS), Lawrence Berkeley National Laboratory		X-ray energy: 25-30 keV
Optical microscope	Leica		to mount the gasket and load samples
Pt powder	thermofisher	38374
Reaction kettle	Xian Yichuang Co.,Ltd.		50 mL
Sand paper			from 400 mesh to 1000 mesh
Transmission Electron Microscopy	FEI		Titan G2 60-300
Two-dimension image plate	ALS, BL 12.2.2		mar 345