Inducción de microstreaming por oscilaciones de burbujas no esféricas en un sistema de levitación acústica

Resumen

Se propone una técnica rápida y fiable para controlar las oscilaciones de forma de una sola burbuja acústica atrapada que se basa en la técnica de coalescencia entre dos burbujas. Las oscilaciones en forma de burbuja controladas por simetría y estado estacionario permiten analizar el flujo de fluido generado en las proximidades de la interfaz de burbuja.

Resumen

Cuando se encuentran cerca de barreras biológicas, las microburbujas oscilantes pueden aumentar la permeabilidad de la membrana celular, lo que permite la internalización de fármacos y genes. Las observaciones experimentales sugieren que la permeabilización temporal de estas barreras puede deberse al esfuerzo cortante que se ejerce sobre los tejidos celulares por micrortransmisión de cavitación. La micrortransmisión de cavitación es la generación de flujos de vórtice que surgen alrededor de microburbujas de ultrasonido oscilantes. Para producir tales flujos de líquido, las oscilaciones de burbujas deben desviarse de las oscilaciones puramente esféricas e incluir una inestabilidad de traslación o modos de forma. Los estudios experimentales de flujos inducidos por burbujas y esfuerzo cortante en superficies cercanas a menudo están restringidos en su alcance debido a la dificultad de capturar las deformaciones de forma de las microburbujas de una manera estable y controlable. Describimos el diseño de una cámara de levitación acústica para el estudio de oscilaciones no esféricas controladas por simetría. Dicho control se realiza mediante el uso de una técnica de coalescencia entre dos burbujas que se aproximan en un campo de ultrasonido suficientemente intenso. El control de oscilaciones no esféricas abre el camino a una micrortransmisión de cavitación controlada de una microburbuja oscilante de superficie libre. Las cámaras de alta velocidad de cuadro permiten investigar casi simultáneamente la dinámica de burbujas no esféricas en la escala de tiempo acústica y el flujo de líquido en una escala de tiempo más baja. Se muestra que se puede obtener una gran variedad de patrones de fluidos y que están correlacionados con el contenido modal de la interfaz de burbujas. Demostramos que incluso los modos de forma de alto orden pueden crear patrones de fluidos de gran distancia si la dinámica de la interfaz contiene varios modos, destacando el potencial de las oscilaciones no esféricas para la administración de fármacos dirigida y localizada.

Introducción

En medicina, un medicamento administrado debe penetrar muchos obstáculos en el sistema vivo antes de alcanzar los objetivos deseados. Sin embargo, la mayoría de los medicamentos se limpian rápidamente del torrente sanguíneo. La eficiencia de la focalización es baja y no pueden cruzar fácilmente las membranas celulares, lo que lleva a una administración ineficaz de medicamentos. Actualmente, el uso de microburbujas en combinación con ultrasonido ha sido propuesto como un método innovador para la administración no invasiva, precisa y dirigida de fármacos y genes a tejidos y células patológicas¹. En este enfoque, las microburbujas pueden desempeñar un papel como portadores donde los medicamentos libres se inyectan conjuntamente con una suspensión de burbujas de gas o se cargan en su superficie. Las microburbujas también pueden actuar como un vector local para reenfocar la energía del ultrasonido con el fin de interactuar con las células. Básicamente, bajo la exposición al ultrasonido, las burbujas se comprimen y expanden de manera estable, un régimen llamado cavitación estable que genera flujos de líquido y, por lo tanto, tensión de cizallamiento en objetos cercanos. Las microburbujas también pueden oscilar de forma no lineal y expandirse hasta el colapso, en régimen de cavitación inercial, produciendo ondas de choque que se propagan radialmente desde el sitio de colapso². Se ha demostrado que la cavitación, ya sea estable o inercial, mejora la permeabilización de las membranas celulares y, por lo tanto, mejora la internalización de los fármacos en la célula³.

En aplicaciones terapéuticas, comprender el mecanismo de la interacción burbuja-célula es muy importante, pero existen varias barreras, tanto científicas como técnicas, que impiden que nuestro conocimiento avance. En primer lugar, capturar la dinámica de las células en respuesta a estímulos mecánicos inducidos por burbujas es muy difícil⁴. En la escala de tiempo acústica, las oscilaciones de microburbujas de primer orden pueden conducir a la activación de los canales de membrana, facilitando el paso molecular a través de las interfaces biológicas. Esto ocurre a través de la oscilación directa de la membrana celular, también llamada "masaje celular"⁵. La activación del canal después del estrés mecánico directo se evidenció utilizando técnicas de patch-clamp que midieron las propiedades electrofisiológicas de las membranas celulares durante y después de la exposición al ultrasonido⁶. La medición de la dinámica celular inducida por burbujas (es decir, el campo completo de deformación de la membrana celular) en la escala de tiempo acústica, también proporcionaría información sobre el umbral de expansión del área de membrana Δ A/ A requerida para inducir poros en la membrana celular⁷. La segunda barrera es controlar el régimen de colapso de burbujas para evitar la lisis celular inducida por microburbujas. Los colapsos de burbujas y los microchorros inducidos han sido identificados como un mecanismo a través del cual ocurre la perforación de la membrana ^8,9. Una vez permeabilizada, la membrana celular se repara mediante el autosellado del calcio de las bicapas lipídicas y la fusión de vesículas intracelulares⁹. La aparición de colapsos de burbujas también puede causar daños letales a la célula e inducir efectos secundarios innecesarios en los alrededores. En aplicaciones sensibles como la apertura de la barrera hematoencefálica mediada por ultrasonido, generalmente se acepta que se deben evitar los colapsos de burbujas inerciales¹⁰.

Por lo tanto, actualmente se dedican grandes esfuerzos al diseño de secuencias de emisión de ultrasonidos, junto con el monitoreo y control pasivo de la cavitación, para garantizar oscilaciones estables de microburbujas¹¹. En este régimen estable, se ha planteado la hipótesis de que las burbujas oscilantes estables juegan un papel importante en el desencadenamiento de la permeabilización de la membrana al promover el esfuerzo cortante espacialmente dirigido en la membrana celular⁷. El esfuerzo cortante resulta de los flujos de líquido creados en las proximidades de las burbujas oscilantes. Estos flujos de líquido se denominan micrortransmisión de cavitación y, como se mencionó anteriormente, son uno de los varios mecanismos posibles que son responsables de una mayor absorción de moléculas extracelulares. Cuando se trata de la suspensión de burbujas o células, como los ensayos de transfecciones biológicas in vitro¹², la permeabilización por micrortransmisión podría ser mucho más eficiente que la permeabilización por colapso de burbujas. Esto se puede demostrar mediante una simple consideración geométrica. En las suspensiones celulares, la sonoporación será eficiente si la mayoría de las células suspendidas se someten a efectos mecánicos suficientemente grandes (lo que lleva a la permeabilización de la membrana). Se sabe que los colapsos de burbujas se dirigen a lo largo de la dirección de ruptura de la simetría isotrópica, como el eje¹³ de la pared de la burbuja o la burbuja-burbuja y la línea de células burbuja que unen su centro de masa¹⁴. El microchorro producido es, por lo tanto, un fenómeno espacialmente localizado a lo largo de un número finito de líneas que unen los centros celular y de burbuja. Dependiendo de la célula y la concentración de burbujas, así como de la distancia burbuja-celda, este efecto puede no ser el más eficiente para permeabilizar todo el número de células suspendidas. En contraste, la microtransmisión de cavitación es un fenómeno que ocurre en una escala de tiempo lenta, con una gran expansión espacial en comparación con el radio de la burbuja. Además, el flujo de líquido se distribuye alrededor de la burbuja y, por lo tanto, puede afectar a un mayor número de células, a un rango muy largo. Por lo tanto, comprender la microtransmisión de cavitación generada alrededor de una burbuja oscilante es un requisito previo para controlar y cuantificar el esfuerzo cortante inducido por burbujas que se aplica a las células.

Para ello, un paso preliminar consiste en controlar las oscilaciones esféricas y no esféricas de una burbuja impulsada por ultrasonidos, ya que los flujos de líquido generados son inducidos por el movimiento de la interfaz de la burbuja^15,16. En particular, las oscilaciones de forma de las microburbujas deben activarse y mantenerse estables. Además, la orientación de las oscilaciones en forma de burbuja debe controlarse para analizar adecuadamente la correlación entre la dinámica de la interfaz de burbuja y el patrón de microstreaming inducido. Al resumir la literatura existente, es obvio que los resultados experimentales detallados de la microtransmisión inducida por cavitación solo están disponibles para burbujas adheridas a una superficie. Las microburbujas unidas a la pared se usan comúnmente para evaluar la dinámica precisa de la interfaz y las interacciones celulares a escala micrométrica bajo un sistema de microscopía ultrarrápida. Esta configuración es terapéuticamente relevante cuando se consideran microburbujas vibratorias localizadas en la membrana celular^17,18,19. Sin embargo, el estudio de la burbuja unida al sustrato puede complicar el análisis de la dinámica de la burbuja, en parte debido a la naturaleza compleja de la dinámica de la línea de contacto²⁰ y al desencadenamiento de modos de forma asimétrica²¹. En aplicaciones médicas y biológicas, las burbujas que no están unidas a una pared se encuentran comúnmente en geometrías confinadas, como vasos pequeños. Esto afecta significativamente la dinámica de burbujas y las inestabilidades de forma. En particular, la presencia de una pared cercana cambia el umbral de presión para el modo de forma, lo que se activa a valores de presión más bajos según el número de modo de forma y el tamaño de burbuja²². La pared también afecta el microstreaming inducido por burbujas con posiblemente mayor intensidad para el flujo producido²³.

Entre todos los posibles escenarios que pueden experimentar las microburbujas (libres o adheridas, cerca de una pared, colapsando o oscilando establemente), proponemos investigar la dinámica no esférica de una sola burbuja lejos de cualquier límite. La configuración experimental se basa en un sistema de levitación acústica²⁴ en el que se utiliza una onda de ultrasonido estacionaria para atrapar la burbuja. Este escenario es consistente con aplicaciones médicas en las que una colección de burbujas y células suspendidas coexisten en una cámara de sonotransfección, por ejemplo. En la medida en que las burbujas y las células no están demasiado cerca, se supone que la presencia de una célula no afecta la dinámica de la interfaz de burbujas. Cuando las células siguen las trayectorias en forma de bucle de la micrortransmisión inducida por cavitación, se acercan cíclicamente y repelen desde la ubicación de la burbuja y podemos suponer que la presencia celular no afecta ni al patrón de transmisión ni a su velocidad media. Además, la dinámica no esférica y la microtransmisión inducida desde burbujas individuales lejos del límite son bien conocidas desde un punto de vista teórico. Para vincular el flujo de líquido inducido por burbujas a la dinámica del contorno de burbujas, se requiere caracterizar con precisión la dinámica de la interfaz de burbujas. Para ello, es preferible adaptar la escala espaciotemporal en estudios experimentales con respecto a los utilizados en terapéutica para que la adquisición con cámaras comunes de alta velocidad (por debajo de 1 millón de fotogramas/segundo) sea posible mediante el uso de grandes burbujas excitadas a frecuencias más bajas. Cuando se consideran burbujas no recubiertas, la frecuencia propia ω n de un modo _n dado está relacionada con el tamaño de la burbuja como 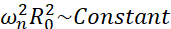²⁵. Esta relación radio-frecuencia propia se modifica ligeramente cuando se consideran las burbujas con cáscara²⁶, pero el orden de magnitud de la frecuencia propia ω_n sigue siendo el mismo. Por lo tanto, la investigación de burbujas con radios de equilibrio ~ 50μm en un campo de ultrasonido de 30 kHz es similar al estudio de burbujas recubiertas de radios ~ 3μm en un campo de 1.7 MHz, como propone Dollet et ^al.27. Por lo tanto, se esperan números de modo de forma similares y, por lo tanto, patrones de microtransmisión.

Para desencadenar oscilaciones no esféricas de la interfaz de burbuja, es necesario exceder un cierto umbral de presión que depende del radio, como se muestra en la Figura 1. Las técnicas experimentales existentes se basan en el aumento de la presión acústica para activar los modos de superficie (ilustrado por la trayectoria (1) en la Figura 1), ya sea por aumento de presión paso a paso²⁸ o por excitación de amplitud modulada responsable del inicio periódico y la extinción de los modos de superficie²⁹. Los principales inconvenientes de estas técnicas son (i) una orientación aleatoria del eje de simetría de las oscilaciones superficiales que no se puede controlar para que estén en el plano de imagen, (ii) una corta vida útil de las oscilaciones en forma de burbuja que dificulta el análisis de los flujos de líquido inducidos en escalas de tiempo más grandes, y (iii) la activación frecuente de modos de forma inestables. Proponemos una técnica alternativa para cruzar el umbral de presión a una presión acústica constante en el mapa de radio/presión, como se ilustra en la trayectoria (2) de la Figura 1. Para ello, se requiere aumentar el tamaño de la burbuja de tal manera que esté en la zona de inestabilidad. Tal aumento se realiza mediante una técnica de coalescencia de burbujas. La coalescencia de dos microburbujas, inicialmente oscilantes esféricamente, se explota para crear una sola burbuja deformada. Si la presión acústica y el tamaño de burbuja de la burbuja fusionada están en la zona de inestabilidad, se activan los modos de superficie. También evidenciamos que la técnica de coalescencia induce oscilaciones de forma estables en un régimen de estado estacionario, así como un eje de simetría controlado definido por el movimiento rectilíneo de las dos burbujas que se aproximan. Debido a que se garantiza una oscilación de forma estable durante minutos, el análisis del flujo de fluido inducido por burbujas es posible sembrando el medio líquido con micropartículas fluorescentes, iluminadas por una lámina láser delgada. El registro del movimiento de las micropartículas sólidas en las proximidades de la interfaz de burbujas permite identificar el patrón del flujo de fluido inducido³⁰. El principio general de la activación de oscilaciones en forma de burbuja, que conduce a un flujo de fluido estable en el tiempo, se ilustra en la Figura 2.

En el siguiente protocolo, describimos los pasos necesarios para crear oscilaciones estables en forma de burbuja a través de la técnica de coalescencia y describimos las mediciones del flujo de fluido. Esto incluye el diseño del sistema de levitación acústica, la calibración acústica, la nucleación de burbujas y la técnica de coalescencia, la medición de la dinámica de la interfaz de burbujas y el flujo de fluido circundante, y el procesamiento de imágenes.

Protocolo

1. Diseño de la cámara de levitación acústica

1. Diseñe un tanque cúbico ópticamente transparente (similar al PMMA) (8 cm de borde y 2,8 mm de espesor por cara) con el módulo de geometría de un software de simulación multifísica (Tabla de materiales).
2. Inserte una superficie cilíndrica (Ø = 35 mm) centrada en la parte inferior del tanque, para modelar el transductor ultrasónico.
3. Ajuste las condiciones de contorno a presión cero en cada pared con un desplazamiento normal de amplitud de 1 μm en la superficie del transductor.
4. Usando un módulo de dominio de frecuencia, simule la función de respuesta de frecuencia (FRF) del tanque en el rango de frecuencia [10 - 40] kHz, en las tres ubicaciones arbitrarias loc1 = (0.01375, 0.01375, 0.04125), loc2 = (0, 0, 0.0088) y loc3 = (0.021725, 0.023375, 0.00935).
5. Adapte el tamaño del tanque de tal manera que uno de los modos acústicos de la cavidad corresponda a la frecuencia nominal del transductor (aquí 31.2 kHz). Por lo tanto, el FRF contiene un pico de resonancia cercano a esta frecuencia, como se ilustra en la Figura 3.
6. Trazar el campo de presión dentro del tanque, como se muestra en la Figura 4. El modo de resonancia elegido debe contener al menos un antinodo de presión en el interior del recipiente, en el que quedará atrapada la burbuja acústica.
7. Al diseñar el tanque, diseñe una cara superior móvil con una ranura guía en cada borde para cerrar firmemente las caras del tanque. Perfore un pequeño orificio en la cara superior para llenar el tanque con el medio líquido.
8. Coloque el tanque de agua encima de un marco casero que contenga el transductor de ultrasonido (tipo Langevin, frecuencia nominal de 31.2 kHz). Use gel ecográfico para acoplar el transductor a la pared inferior del tanque.
9. Coloque el tanque y el sistema de bastidor sobre una mesa de desplazamiento de tres direcciones con tornillos micrométricos.
10. Llene el tanque con agua microfiltrada, desmineralizada y (no desgasificada, volumen ~ 500 ml, saturación de oxígeno de aproximadamente 8 mg · ^L-1).
    NOTA: El uso de agua no desgasificada en lugar de desgasificada permite mantener burbujas estables durante la duración de los experimentos. El uso de agua desgasificada acelerará la contracción de las burbujas debido a la difusión de gas, incluso si se contrarresta ligeramente con la difusión rectificada (mediada por ultrasonido).

2. Generación de burbujas y calibración acústica

1. Preparar la configuración experimental utilizada para la nucleación de burbujas inducida por láser, la excitación acústica y la grabación de alta velocidad (Figura 5a, b, c). La configuración experimental consiste en (A) el sistema de levitación acústica, (B) la fuente de alimentación láser y (C) el cabezal láser, (D) una lente cóncava esférica, (E) una lente plano-cóncava y una lente asférica, (F) la cámara de alta velocidad, (G) el diodo emisor de luz continuo. Posteriormente, para las mediciones de flujos de líquido (Figura 5d) (H) se añadirá una fuente láser de onda continua, (I) una lente cilíndrica plano-cóncava seguida de una lente cilíndrica plano-cóncava insertada detrás de la primera lente y orientada en el eje ortogonal.
2. Conecte el transductor de ultrasonido a un generador de funciones. Ajuste la señal de excitación como: forma de onda sinusoidal, onda continua, frecuencia 31.2 kHz. La amplitud es el único parámetro variable.
3. Coloque la lente (D) a una distancia aproximada de 6 cm delante del cabezal láser (C).
4. Coloque la lente (E) a una distancia aproximada de 12 cm delante de la lente (D).
5. Coloque el tanque de agua (A) de tal manera que un punto de enfoque del láser se encuentre dentro del tanque de agua, lo que lleva a la generación de chispas para cada pulso láser (5 -10 mJ). La chispa láser debe ubicarse aproximadamente 3 cm por debajo del antinodo de presión objetivo.
   NOTA: Sin ultrasonido (US), la burbuja nucleada con láser se elevará a la cara superior debido a la flotabilidad.
6. Encienda el transductor de ultrasonido. Aumente el voltaje aplicado hasta que la burbuja ya no se eleve verticalmente, sino que se desvíe hacia el antínodo de presión y, para una presión suficientemente alta, quede atrapada.
7. Ajuste la iluminación retroiluminada (diodo emisor continuo de luz) y la cámara de alta velocidad para observar la burbuja atrapada.
   NOTA: Al nuclear una nueva burbuja con una chispa láser, es fácil capturar la trayectoria de la burbuja acercándose a su ubicación de captura.
8. Mueva la ubicación de la chispa láser dentro del tanque de agua de modo que la trayectoria de la burbuja permanezca dentro del plano focal de la cámara.
9. Atrapa una burbuja y captura sus oscilaciones radiales con los siguientes parámetros: tamaño de fotograma 128 x 128 píxeles, velocidad de adquisición 180 kHz. En la Figura 6 se proporciona un ejemplo de oscilaciones radiales de gran amplitud durante dos períodos acústicos. El tamaño típico de las burbujas de gas varía de 30 a 80 μm.
10. Grabe las oscilaciones radiales de burbujas durante 3 a 30 milisegundos para capturar cientos o miles de oscilaciones de burbujas. Repita esta grabación para aumentar los voltajes aplicados del transductor. Los voltajes aplicados típicos están en el rango de 0 - 8 V.
    NOTA: Al modificar el voltaje aplicado, la ubicación de equilibrio de la burbuja atrapada se mueve ligeramente verticalmente. Para seguir las oscilaciones sin mover la iluminación retroiluminada y la cámara, coloque el sistema (transductor y tanque de agua) en una mesa móvil de tres direcciones con precisión micrométrica.
11. Encienda el transductor de ultrasonido y capture una imagen del fondo para el análisis posterior.
12. Vuelva a procesar la serie de vídeos siguiendo este procedimiento:
    1. Ejecute el archivo ejecutable VoltagePressure.exe. La interfaz que se muestra en la figura 7 debería abrirse.
       NOTA: El script está disponible como documento complementario.
    2. Especifique los parámetros físicos y experimentales en la columna izquierda (Figura 7A).
    3. Especifique los valores de voltaje aplicado para la serie de registros en la tabla inferior derecha (Figura 7B).
    4. En el panel de análisis de radio de burbuja, haga clic en Parámetros de carga (Figura 7C) y seleccione la carpeta que contiene todos los archivos de su serie de videos, y luego la imagen de fondo (obligatorio).
    5. Se permite elegir entre analizar todos los videos a la vez, haciendo clic en Auto, o uno por uno haciendo clic en Paso a paso.
    6. Para cada archivo de vídeo, la evolución del radio de la burbuja se traza en un período acústico, y se superpone un ajuste numérico. La curva roja corresponde a un modelado linealizado de Rayleigh-Plesset. Se muestra el radio de burbuja de equilibrio (Figura 7D).
    7. De acuerdo con el ajuste numérico, la presión aplicada para este voltaje se muestra en el panel gráfico Presión (Voltaje) (Figura 7E). El valor de la presión aplicada también se muestra en la tabla inferior derecha (Figura 7B). Las presiones aplicadas típicas correspondientes a la dinámica de voltaje de 0 a 8 V son de 0 a 25 kPa.
    8. Una vez que se hayan procesado todos los videos, haga clic en el botón Regresión lineal para realizar un ajuste lineal de la curva de presión / voltaje. Los datos (valores de voltaje y presión) se guardan en un archivo .txt ubicado en el directorio actual. Se proporciona la pendiente del ajuste.

3. Técnica de coalescencia

1. Encienda el transductor de ultrasonido. Ajuste la tensión aplicada lo suficientemente alta como para que la presión acústica correspondiente pueda provocar la activación de la inestabilidad superficial, de acuerdo con el diagrama numérico de presión/radio de las zonas de inestabilidad, como se muestra en la figura 8.
2. Nuclear una burbuja, que luego migrará a su lugar de captura. Si la burbuja atrapada solo exhibe oscilaciones esféricas, pase al siguiente paso. Si aparecen oscilaciones no esféricas:
   1. Apague la potencia del ultrasonido para permitir que la burbuja suba a la superficie superior.
   2. Modifique la energía del láser (ajustando finamente unos pocos mJ) o reduzca el voltaje del transductor.
   3. Encienda la alimentación del ultrasonido.
   4. Nuclear una nueva burbuja.
   5. Repita este procedimiento hasta que el tamaño de la burbuja provoque oscilaciones puramente esféricas.
3. Cuando una burbuja atrapada exhibe solo oscilaciones esféricas, genere una nueva chispa láser. Cuando la nueva burbuja alcanza el lugar de captura, se produce la coalescencia.
4. Si la burbuja fusionada exhibe solo oscilaciones esféricas, genere una nueva burbuja. Pueden ser necesarias múltiples coalescencias para alcanzar el radio de burbuja en el que se producen las deformaciones no esféricas. Un ejemplo de coalescencia de burbujas que conduce a oscilaciones no esféricas se muestra en la Figura 9.
5. Una vez que la burbuja fusionada exhiba oscilaciones no esféricas, registre las oscilaciones de la burbuja durante aproximadamente 3 a 30 milisegundos.
6. Identifique el número de modo de oscilaciones de forma consultando la figura 10.

4. Mediciones de flujo de fluido

1. En el caso de las mediciones de micrortransmisión de cavitación, se deben agregar partículas trazadoras fluorescentes al agua antes de la nucleación de burbujas. En este estudio, se utilizan partículas de 0,71 μm (Tabla de materiales). Son lo suficientemente pequeños para ser acústicamente transparentes (no influenciados por la fuerza de radiación acústica) y para seguir con precisión el flujo, así como lo suficientemente grandes como para dispersar la luz láser. Utilice tres gotas para el volumen del tanque de agua, correspondientes a aproximadamente 2.10⁴ partículas/mm³.
2. Antes de tomar medidas, establezca los siguientes parámetros para capturar tanto la dinámica de burbujas (escala de tiempo rápida) como el flujo de fluido (escala de tiempo baja):
   1. Cree una partición del disco de grabación de la cámara.
   2. Alternativamente, defina los parámetros de grabación como:
      1. Velocidad de fotogramas 180 kHz, tamaño de fotograma 128 x 128 píxeles y tiempo de exposición de 1 μs para una grabación de la dinámica de la interfaz de burbuja
      2. Velocidad de fotogramas 600 Hz, tamaño de fotograma 1024 x 768 píxeles y tiempo de exposición de 1 ms para una grabación del movimiento de los trazadores de tinte.
3. Utilice un láser continuo.
4. Cree una lámina láser delgada dejando pasar sucesivamente el rayo láser a través de la lente cilíndrica plano-cóncava y la lente cilíndrica plano-convexa orientada en un eje ortogonal. Se puede obtener un ancho de haz de aproximadamente 160 μm.
5. Configure la hoja láser para que corresponda al plano de imagen:
   1. Coloque el láser en un dispositivo móvil para que la lámina láser se pueda mover paralelamente al plano de imagen.
   2. Ajuste la posición para que las partículas iluminadas sean visibles por la cámara.
   3. Nuclear y atrapar una burbuja.
   4. Ajuste aún más la posición de la lámina láser, de modo que una sombra se haga visible detrás de la burbuja. La burbuja está ahora dentro de la lámina láser, como se muestra en la Figura 11.
6. Inducir la coalescencia de burbujas hasta que se observe un modo de forma oscilante estable.
7. Haz varias grabaciones cambiando de un lado a otro entre la dinámica de burbujas y la microtransmisión.
   NOTA: Apague el láser continuo cuando no sea necesario. El calentamiento puede crear flujos convectivos no deseados. Además, apague el diodo emisor de luz cuando realice las mediciones del flujo de transmisión.

5. Procesamiento de imágenes para visualizar los patrones de microstreaming de cavitación

1. Instale el software de visualización ImageJ para el procesamiento y análisis de imágenes en Java. También instale el complemento CINE File Reader para abrir los archivos de la cámara de alta velocidad.
2. Haga clic en Archivo | Importar | CineFile y seleccione el vídeo *.cine que contiene la captura del movimiento de la partícula.
3. Seleccione Usar pila virtual en la nueva ventana, el video ahora está cargado.
4. Para observar el movimiento de la partícula sin mostrar el patrón de transmisión, haga clic en Imagen | Ajustar | Brillo/contraste | Automático. El fondo oscuro ahora se reemplaza por una imagen optimizada automáticamente.
5. Para mostrar el patrón resultante, haga clic en Imagen | Pilas | Z Project y elija la opción Max Intensity para la proyección de la imagen. Se muestra una imagen de salida con píxeles que contiene el valor máximo sobre todas las imágenes de la pila. Ajuste el contraste de la imagen como se describe en el paso 5.4, si es necesario.
   NOTA: Se obtiene un patrón de transmisión como los que se muestran en la figura 12b y la figura 12d.

Resultados

En la Figura 9 se presenta una secuencia completa de coalescencia de burbujas que conduce a oscilaciones no esféricas estables en el tiempo y controladas por simetría. La fase de aproximación de dos burbujas oscilantes esféricamente termina cuando se rompe la delgada película líquida entre las dos burbujas. Vale la pena señalar que, en la última etapa anterior a la coalescencia, las interfaces de burbuja se desvían de la esfericidad. Ambas burbujas s...

Discusión

El procedimiento presentado consiste en utilizar la coalescencia de burbujas para desencadenar oscilaciones en forma de burbuja controladas por simetría en estado estacionario, lo que permite estudiar el flujo de fluido a largo plazo inducido por estas oscilaciones. El principal desafío en la técnica es el control de oscilaciones no esféricas para una burbuja atrapada, lejos de cualquier límite.

La mayoría de las técnicas existentes propuestas en la literatura se centraron en burbujas u...

Materiales

Name	Company	Catalog Number	Comments
Aspherical lens	Thorlabs	AL4050	Lens of focus 40 mm
Continuous wave laser source	CNI	MLL6FN	DPSS laser of wavelength 532nm, energy 400 mW
Cylindrical plano-concave lens	Thorlabs	LJ1277L1-A	lens of focus -25?4mm
Cylindrical plano-concave lens	Thorlabs	LK1900L1	lens of focus 250 mm
Fluorescent particles	Duke Scientific	R700	Red polymer fluorescent microspheres
Function generator	Agilent	HP33120	Generator of function feeding the ultrasound transducer
High-speed camera	Vision Research	Phantom v12.0	High-speed recording up to 1 Mfps
Liquid medium	Carlo Erba	Water for analysis	Demineralized, undegassed water
Multiphysics software	Comsol	None	Softwate for simulating the acoustic field of the levitation chamber
Nd:Yag pulsed laser	New Wave Research	Solo III-15	5 ns pulse duration, λ=532 nm, 3.5 mm beam diameter, up to 50 mJ
Plano-concave lens	Thorlabs	N-BK7	lens of focus 125 mm
Spherical concave lens	Thorlabs	N-SF11	Bi-concave lens of focus -25mm
Ultrasound transducer	SinapTec	Custom-made	Nominal frequency 31kHz, active area 35mm diameter
Visualization software	NIH	ImageJ	Software for image processing and analysis in Java
XY Linear stage	Newport	M-406	Displacement stage with micrometric screw
Z-axis linear stage	Edmund Optics	62-299	Vertical displacement stage with micrometric screw