Caracterización viscoelástica de fantasmas de gelatina que imitan tejidos blandos mediante elastografía por indentación y resonancia magnética

Resumen

Este artículo presenta una demostración y resumen de los protocolos de fabricación de fantasmas de gelatina que imitan los tejidos blandos, y la correspondiente caracterización viscoelástica mediante indentación y elastografía por resonancia magnética.

Resumen

La caracterización de las propiedades biomecánicas de los tejidos biológicos blandos es importante para comprender la mecánica tisular y explorar los mecanismos biomecánicos relacionados con la enfermedad, las lesiones y el desarrollo. El método de prueba mecánica es la forma más sencilla para la caracterización de tejidos y se considera como verificación para la medición in vivo . Entre las muchas técnicas de prueba mecánica ex vivo , la prueba de indentación proporciona una forma confiable, especialmente para muestras que son pequeñas, difíciles de fijar y viscoelásticas, como el tejido cerebral. La elastografía por resonancia magnética (ERM) es un método utilizado clínicamente para medir las propiedades biomecánicas de los tejidos blandos. Sobre la base de la propagación de ondas cortantes en tejidos blandos registrada mediante MRE, las propiedades viscoelásticas de los tejidos blandos se pueden estimar in vivo basándose en la ecuación de onda. Aquí, las propiedades viscoelásticas de los fantasmas de gelatina con dos concentraciones diferentes se midieron mediante MRE y sangría. Se han presentado los protocolos de fabricación fantasma, pruebas y estimación del módulo.

Introducción

La mayoría de los tejidos biológicos blandos parecen tener propiedades viscoelásticas que son importantes para comprender su lesión y desarrollo ^1,2. Además, las propiedades viscoelásticas son biomarcadores importantes en el diagnóstico de una variedad de enfermedades como la fibrosis y el cáncer 3,4,5,6. Por lo tanto, la caracterización de las propiedades viscoelásticas de los tejidos blandos es crucial. Entre las muchas técnicas de caracterización utilizadas, las pruebas mecánicas ex vivo de muestras de tejido y la elastografía in vivo utilizando imágenes biomédicas son los dos métodos ampliamente utilizados.

Aunque se han utilizado varias técnicas de prueba mecánica para la caracterización de tejidos blandos, los requisitos para el tamaño de la muestra y las condiciones de prueba no son fáciles de cumplir. Por ejemplo, las pruebas de cizallamiento deben tener muestras fijadas firmemente entre las placas de cizallamiento⁷. La prueba biaxial es más adecuada para el tejido de membrana y tiene requisitos específicos de sujeción ^8,9. Una prueba de compresión se usa comúnmente para pruebas de tejidos, pero no puede caracterizar posiciones específicas dentro de una muestra¹⁰. La prueba de indentación no tiene requisitos adicionales para fijar la muestra de tejido y se puede usar para medir muchas muestras de tejido biológico, como el cerebro y el hígado. Además, con una pequeña cabeza penetradora, se podrían probar propiedades regionales dentro de una muestra. Por lo tanto, se han adoptado pruebas de indentación para probar una variedad de tejidos blandos 1,3,11.

La caracterización de las propiedades biomecánicas de los tejidos blandos in vivo es importante para los estudios traslacionales y las aplicaciones clínicas de la biomecánica. Las modalidades de imagen biomédica como la ecografía (US) y la resonancia magnética (RM) son las técnicas más utilizadas. Aunque las imágenes estadounidenses son relativamente baratas y fáciles de llevar a cabo, sufren de bajo contraste y son difíciles de medir órganos como el cerebro. Capaz de obtener imágenes de estructuras profundas, la elastografía por RM (ERM) pudo medir una variedad de tejidos blandos 6,12, especialmente el cerebro^13,14. Con la vibración externa aplicada, MRE podría medir las propiedades viscoelásticas de los tejidos blandos a una frecuencia específica.

Los estudios han demostrado que a 50-60 Hz, el módulo de corte del cerebro normal es ~ 1.5-2.5kPa 5,6,13,14,15 y ~ 2-2.5 kPa para el hígado normal ¹⁶. Por lo tanto, los fantasmas de gelatina que tienen propiedades biomecánicas similares han sido ampliamente utilizados para imitar tejidos blandos para pruebas y validación^17,18,19. En este protocolo, se prepararon y probaron fantasmas de gelatina con dos concentraciones diferentes. Las propiedades viscoelásticas de los fantasmas de gelatina se caracterizaron utilizando un dispositivo electromagnético MRE hecho a medida¹⁴ y un dispositivo de hendidura ^1,3. Los protocolos de prueba podrían usarse para analizar muchos tejidos blandos como el cerebro o el hígado.

Protocolo

1. Preparación fantasma de gelatina

1. Pese la gelatina, el glicerol y el agua de acuerdo con la Tabla 1. Mezclar la gelatina en polvo con agua para obtener la solución de gelatina.
   NOTA: Las concentraciones de los componentes individuales para preparar los dos fantasmas se muestran en la Tabla 1. Cuanto mayor es la concentración de gelatina, más rígido es el fantasma.
2. Calentar la solución de gelatina a 60 °C en un baño maría. Agregue glicerol a la solución de gelatina mientras mantiene la temperatura.
   NOTA: El glicerol estabiliza las mezclas de gelatina aumentando su temperatura de fusión y módulo de cizallamiento¹⁷.
3. Revuelva la solución y caliéntela a 60 °C de nuevo. Vierta la solución mezclada en un recipiente que se utilizará para MRE y pruebas de indentación. Enfríe la solución a temperatura ambiente y espere hasta que la solución se solidifique.

2. Prueba de MRE

1. Coloque la placa de vibración encima del fantasma de gelatina. Asegúrese de que el contacto entre el fantasma y la placa vibratoria sea firme (Figura 1A).
   NOTA: La placa vibratoria está fabricada en Poliamida con una dimensión de 50 x 50 x 5 mm³.
2. Coloque el fantasma de gelatina en la bobina de la cabeza. Coloque esponjas y sacos de arena alrededor del fantasma de gelatina para asegurarse de que el fantasma esté firmemente colocado. Utilice un actuador electromagnético personalizado con una barra de transmisión^14,18. Monte un actuador electromagnético en la bobina de la cabeza. Conecte la barra de transmisión a la placa vibratoria (Figura 1B).
3. Conecte las líneas de alimentación del actuador con el amplificador. Conecte las líneas de control con el controlador (Figura 1C).
4. Configuración de los parámetros del actuador y de la resonancia magnética
   1. Establezca la forma de onda, la frecuencia de vibración y la amplitud en el generador de funciones. Ajuste la amplitud de vibración deseada ajustando el amplificador de potencia.
      NOTA: Aquí, la forma de onda se establece en sinusoidal en el generador de funciones; la frecuencia de vibración se establece en 40 Hz o 50 Hz, y la amplitud se establece en 1,5 Vpp. En el amplificador de potencia, la relación de amplificación se establece en 40%.
   2. Configure el generador de funciones para que funcione en el modo de disparo. Conecte la línea de activación al puerto de disparo externo de la máquina de resonancia magnética.
   3. Ajuste la frecuencia de escaneo MRE (actuador) igual que la del generador de funciones, de modo que el gradiente de codificación de movimiento se sincronice con el movimiento de la placa de vibración.
5. Medición y análisis de datos
   1. Siga los procedimientos rutinarios de posicionamiento por imágenes. Utilice una secuencia de MRE basada en eco de gradiente (GRE) 2D para obtener imágenes del fantasma de gelatina²⁰. Establezca los parámetros de imagen GRE-MRE de la siguiente manera: Ángulo de giro = 30°; TR/TE = 50/31 ms; Campo de visión = 300 mm; Grosor de la rebanada = 5 mm; Tamaño del vóxel = 2,34 x 2,34 mm².
   2. Mida las imágenes de fase en cuatro puntos temporales en un ciclo sinusoidal. Aplique gradientes de codificación de movimiento positivo y negativo en cada punto de tiempo.
   3. En función de la imagen de fase adquirida, elimine la fase de fondo restando las imágenes de fase codificadas positiva y negativa. Desenvuelva la fase con un algoritmo basado en la clasificación de fiabilidad²¹.
   4. Extraiga el componente principal del movimiento aplicando la transformada rápida de Fourier a las imágenes de fase sin ajustar. Filtre la imagen de fase con un filtro de paso de banda digital. Estimar el módulo de corte con un algoritmo de inversión directa (DI) 2D para obtener el módulo de almacenamiento G' y el módulo de pérdida G''^13,14.
      NOTA: La frecuencia de corte del filtro de paso de banda es [0,04 0,08]. El tamaño de la ventana de ajuste del algoritmo DI es 11 x 11.

3. Prueba de sangría

1. Use un punzón circular o una cuchilla quirúrgica para recortar el fantasma de gelatina en una muestra cilíndrica o cuboide, respectivamente. Asegúrese de que el grosor de la muestra esté entre 3 y 10 mm y que el diámetro de la muestra cilíndrica o del lado largo del cuboide sea mayor de 4 mm. Use una cuchilla afilada para recortar la superficie de la muestra para que sea lo más suave posible para la hendidura.
2. Encienda la alimentación del probador de sangría. Realice lo siguiente utilizando el programa de control de penetrador diseñado para automatizar el procedimiento de contacto del penetrador (programa personalizado; consulte Tabla de materiales).
   1. Haga clic en el botón Retroceder en la GUI para inicializar el proceso de calibración (Figura 2B). Lea el valor del sensor láser y escriba el valor en el cuadro Línea base .
      NOTA: Durante el proceso de calibración, la distancia entre el sensor láser y la placa deflectora se ajusta a un valor predefinido específico.
   2. Coloque un portaobjetos de vidrio en la placa deflectora y registre el valor mostrado por el sensor láser. A continuación, coloque la muestra en el portaobjetos de vidrio y colóquelos juntos en la placa deflectora. Lea el valor del sensor láser y escriba este valor en el cuadro Muestra+Diapositiva .
      NOTA: El sensor láser se utiliza para registrar el desplazamiento de la hendidura, pero también se utiliza para medir el grosor de la muestra antes de la prueba.
   3. Tome la diferencia entre los dos valores obtenidos en el paso 3.2.2 como el espesor de la muestra en la región de interés (ROI).
   4. Coloque cuidadosamente la muestra junto con el portaobjetos de vidrio subyacente justo debajo del penetrador y, a continuación, haga clic en el botón Contacto para iniciar el contacto automático entre el penetrador y la superficie de la muestra.
      NOTA: Si el contacto automático no es satisfactorio, es decir, el penetrador presiona profundamente en la muestra o no tiene un contacto, ajuste la posición del penetrador escribiendo un valor en el rango de 0,05-0,1 mm en el cuadro Desplazamiento y repita los pasos 1.2.1-1.2.4.
   5. Sobre la base del espesor de la muestra medida (paso 3.2.3), estime el desplazamiento de la hendidura (es decir, la profundidad total de la hendidura) multiplicando el espesor por la deformación de prueba con sangría (aquí, se establece en ≤8% para mantener la hendidura dentro de la suposición de deformación pequeña).
   6. Escriba los valores de desplazamiento (paso 3.2.5) en el cuadro Desplazamiento (mm). Ajuste el tiempo de relajación a 180 s en el cuadro Tiempo de permanencia . Haga clic en el botón Sangría . El desplazamiento y la fuerza reactiva durante el procedimiento de retención de rampa se registrarán automáticamente y se guardarán en un archivo en la ruta de archivo especificada.
      NOTA: La ruta de archivo se puede predefinir como la ruta para guardar datos de prueba.
3. Exporta los datos de sangría a una hoja de cálculo. Utilice una serie 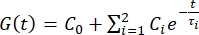de Prony de dos términos para ajustarse a la curva de relajación de la fuerza ^1,3,11: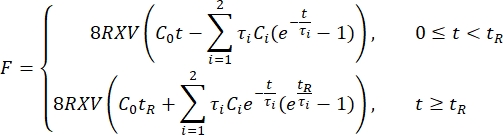
   
4. Estimar el módulo de cizallamiento instantáneo (G ₀) y el módulo de cizallamiento a largo plazo (G_∞) basándose en los parámetros ajustados:
   
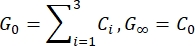
   NOTA: En las ecuaciones anteriores, C ₀, C i y τ_i son parámetros del modelo de la serie Prony, F es la fuerza de indentación, R es el radio del penetrador, X es el factor de compensación para el supuesto de medio espacio infinito, V es la velocidad de indentación, t es la variable de tiempo y t _R es el tiempo de rampa.

Resultados

Siguiendo el protocolo MRE, se observó una clara propagación de onda de corte en los fantasmas de gelatina a 40 y 50 Hz (Figura 3). Las propiedades viscoelásticas medidas a partir de MRE, y las pruebas de indentación se muestran en la Figura 4. Los valores estimados de G' y G" en cada prueba para cada fantasma se resumen en la Tabla 2. Siguiendo el protocolo de indentación, las propiedades viscoelásticas de cada fantasma en cada punto de p...

Discusión

Los fantasmas de gelatina se utilizan comúnmente como materiales que imitan el tejido para probar y validar algoritmos y dispositivos 17,19,22,23,24,25,26,27. Uno de los estudios pioneros que utilizaron el fantasma de gelatina para comparar la ERM y las pr...

Materiales

Name	Company	Catalog Number	Comments
24-channel head & Neck coil	United Imaging Healthcare	100120	Equipment
3T MR Scanner	United Imaging Healthcare	uMR 790	Equipment
Acquisition board	Advantech Co	PCI-1706U	Equipment
Computer-Windows	HP	790-07	Equipment
Electromagnetic actuator	Shanghai Jiao Tong University		Equipment
Function generator	RIGOL	DG1022Z	Equipment
Gelatin	CARTE D’OR		Reagent
Glycerol	Vance Bioenergy Sdn.Bhd		Reagent
Indenter control program	custom-designed		Software; accessed via: https://github.com/aaronfeng369/FengLab_indentation_code.
Laser sensor	Panasonic	HG-C1050	Equipment
Load cell	Transducer Technique	GSO-10	Equipment
MATLAB	Mathworks		Software
Power amplifier	Yamaha	A-S201	Equipment
Voice coil electric motor	SMAC Corporation	DB2583	Equipment