Se requiere una suscripción a JoVE para ver este contenido. Inicie sesión o comience su prueba gratuita.
Method Article
Enfoque de modelado de elementos finitos basado en imágenes de ultrasonido intravascular para cuantificar in vivo las propiedades mecánicas de la arteria coronaria humana
* Estos autores han contribuido por igual
En este artículo
Resumen
Las imágenes de ultrasonido intravascular in vivo muestran el movimiento de la sección transversal coronaria correspondiente a diferentes condiciones de carga de presión. Sobre la base de un modelo de elementos finitos, se empleó un esquema iterativo para determinar las propiedades mecánicas específicas del paciente de las arterias coronarias in vivo mediante la comparación del movimiento coronario del modelo computacional y las imágenes médicas.
Resumen
La cuantificación de las propiedades mecánicas de las paredes arteriales coronarias podría proporcionar información significativa para el diagnóstico, el manejo y el tratamiento de las enfermedades de las arterias coronarias. Dado que no se dispone de muestras coronarias específicas del paciente para los pacientes que requieren una monitorización continua, es imposible realizar pruebas experimentales directas de las propiedades del material de los vasos. Los modelos coronarios actuales suelen utilizar parámetros de materiales de la literatura disponible, lo que conduce a errores significativos en el cálculo de la tensión/deformación mecánica. Aquí, presentaríamos un enfoque de actualización basado en modelos de elementos finitos (FEMBUA) para cuantificar las propiedades materiales in vivo específicas del paciente de las arterias coronarias basadas en imágenes médicas. Se adquirieron imágenes de ultrasonido intravascular (IVUS) e histología virtual (VH)-IVUS de las arterias coronarias de un paciente con enfermedad de las arterias coronarias. Se segmentaron las imágenes de IVUS que mostraban el movimiento vascular a lo largo de un ciclo cardíaco y se seleccionaron dos fotogramas de IVUS con circunferencias lumínicas máximas y mínimas para representar la geometría coronaria en condiciones de presión sistólica y diastólica, respectivamente. También se segmentó la imagen VH-IVUS para obtener los contornos de los vasos, y se añadió un espesor de capa de 0,05 cm a los contornos VH-IVUS para reconstruir la geometría coronaria. Se creó un modelo computacional de elementos finitos con un modelo anisotrópico de material de Mooney-Rivlin utilizado para describir las propiedades mecánicas del vaso y las condiciones de presión arterial pulsátil prescritas a la superficie luminal coronaria para hacer que se contraiga y expanda. Luego, se empleó un enfoque de actualización iterativa para determinar los parámetros del material del modelo anisotrópico de Mooney-Rivlin haciendo coincidir las circunferencias mínimas y máximas de lúmenes del modelo computacional de elementos finitos con las de las imágenes de cine IVUS. Este enfoque de actualización basado en modelos de elementos finitos basado en imágenes podría extenderse con éxito para determinar las propiedades de los materiales de las paredes arteriales en varios lechos vasculares y tiene el potencial para la evaluación del riesgo de enfermedades cardiovasculares.
Introducción
La enfermedad de las arterias coronarias (EAC) es una de las principales causas de mortalidad y morbilidad, y fue responsable de más de 9,14 millones de muertes en 2019 en todo el mundo 1,2. El desarrollo de enfermedades de las arterias coronarias, como la aterosclerosis y la estenosis, suele ir acompañado de alteraciones en las fuerzas mecánicas y cambios en las propiedades del material de la pared vascular3. Las propiedades materiales de las arterias coronarias no solo son la piedra angular para determinar su respuesta mecánica a la carga fisiológica, sino también los elementos clave para simular el comportamiento mecánico de los vasos sanguíneos, predecir el desarrollo de lesiones ateroscleróticas y evaluar el efecto terapéutico de diversos dispositivos médicos 4,5. En consecuencia, una comprensión profunda y una cuantificación precisa de las propiedades del material coronario tienen un valor primordial para el diagnóstico precoz de la enfermedad, la medicina de precisión y la evaluación del pronóstico6.
Los experimentos mecánicos de tejidos coronarios aislados, como la prueba biaxial plana, la prueba de indentación, la prueba de extensión de inflado y la prueba de extensión uniaxial, son enfoques comunes para cuantificar las propiedades mecánicas de las paredes de los vasos coronarios ex vivo 7,8,9. A partir de estos enfoques, se obtuvieron muestras de arterias coronarias de pacientes o animales de experimentación. Se llevaron a cabo ensayos mecánicos para determinar las respuestas de deformación de la pared del recipiente bajo diferentes condiciones de tensión, y luego se determinaron los parámetros del material mediante el ajuste de los datos experimentales10. Estudios previos han demostrado que las propiedades coronarias son altamente no lineales y anisotrópicas11. Aunque los experimentos ex vivo pueden proporcionar datos precisos sobre las propiedades de los materiales, también existen limitaciones significativas, que son las siguientes: en primer lugar, el comportamiento mecánico de la muestra después de extraerla de los sujetos vivos sería diferente al de las condiciones in vivo, lo que puede afectar a la precisión de los resultados de las pruebas. En segundo lugar, debido a las limitaciones éticas y prácticas, es difícil obtener una gran colección de tejidos normales o patológicos de las arterias coronarias para realizar las pruebas mecánicas.
Para superar estas limitaciones, los investigadores han explorado técnicas novedosas para la cuantificación in vivo, en tiempo real y específica del paciente de las propiedades del material coronario. Entre ellos, el enfoque de actualización basado en modelos de elementos finitos (FEMBUA) basado en imágenes médicas promete abordar estos problemas desafiantes. Este abordaje hace uso de técnicas de imagen avanzadas como la ecografía intravascular (IVUS) y la histología virtual (VH)-IVUS para capturar la geometría coronaria detallada, la composición de los tejidos y su movimiento12. Mediante la construcción de modelos 3D de elementos finitos (FE) y la incorporación de condiciones fisiológicas de presión arterial específicas del paciente, se pudo recuperar el comportamiento vascular dinámico durante los ciclos cardíacos optimizando los parámetros del material para que coincidan con los datos de imagen para una cuantificación rápida y precisa de las propiedades del material coronario13. Las ventajas del enfoque de actualización de FE in vivo sobre los experimentos ex vivo incluyen la evaluación in vivo sin escisión de tejidos, la facilitación de evaluaciones a gran escala y la simulación de la dinámica vascular en condiciones complejas para ayudar a la comprensión de la fisiopatología de las enfermedades coronarias.
En este artículo, se presentan los pasos clave del enfoque de actualización basado en modelos de elementos finitos, que incluyen una segmentación y procesamiento detallados de imágenes de cine IVUS y VH-IVUS, reconstrucción del modelo computacional de estructura de capa delgada solamente, ejecución del esquema iterativo para buscar parámetros de material óptimos para los tejidos arteriales coronarios. El objetivo de este protocolo es cuantificar las propiedades materiales de la arteria coronaria de una muestra de paciente con EAC utilizando el método FEMBUA como demostración, especialmente la ilustración de métodos paso a paso. Concluimos discutiendo la importancia y otros aspectos de este método in vivo .
La participante seleccionada es una mujer de 64 años sin antecedentes clínicos previos de enfermedad coronaria. Este paciente fue diagnosticado con enfermedad de las arterias coronarias después de tener síntomas de dolor torácico. Se realizó coronariografía y gammagrafía IVUS para confirmar el diagnóstico. Se encontró una lesión en placa con estenosis del 60% en el centro de la arteria descendente anterior izquierda. Después de la evaluación, se adoptó el tratamiento médico óptimo para tratar al paciente.
Protocolo
Los datos clínicos no identificados, incluidas las imágenes de IVUS in vivo y los datos de presión arterial, se obtuvieron de un paciente con EAC en el Hospital de Zhongda, Universidad del Sureste, con el consentimiento informado obtenido. El paciente de muestra fue seleccionado de la lista de pacientes de un estudio clínico sobre lesiones ateroscleróticas coronarias intermedias para demostrar el método para cuantificar las propiedades del material de los vasos coronarios específicos del paciente14. El estudio se llevó a cabo siguiendo el protocolo aprobado por el Comité de Ética de Investigación Clínica del Hospital de Zhongda, Universidad del Sureste (número de aprobación: 2017ZDSYLL023-p01).
1. Adquisición y tratamiento de datos
- Adquisición de imágenes Cine IVUS y VH-IVUS
- Colocar el catéter IVUS distal a la lesión aterosclerótica con la guía de una angiografía coronaria y tirar de él hacia el lado proximal. Genere imágenes de IVUS en escala de grises a lo largo del camino para visualizar la sección transversal del vaso coronario.
- Utilice el sistema de imágenes IVUS equipado con un catéter de platino 2.9F de 20 MHz de alto rendimiento para adquirir imágenes IVUS del segmento arterial coronario con placa aterosclerótica del paciente con EAC (Figura 1).
- Durante la adquisición de la imagen de IVUS, detenga el catéter en el sitio de la lesión preseleccionado durante aproximadamente 2 s para obtener una secuencia de imágenes de IVUS llamada cine IVUS. Las imágenes de cine IVUS mostraron claramente los cambios dinámicos de la sección transversal en el sitio de la placa dada a lo largo del ciclo cardíaco.
- Genere imágenes VH-IVUS basadas en fotogramas IVUS adquiridos en el instante del pico R en electrocardiogramas para visualizar los componentes de la placa en forma codificada por colores utilizando el sistema de imágenes.
NOTA: Las imágenes VH-IVUS proporcionan un mapa de color intuitivo para cuatro componentes clave de la placa en la placa aterosclerótica: núcleo necrótico rico en lípidos (lípido) en rojo, calcificación en blanco, tejido fibroso en verde oscuro y tejido adiposo fibroso en verde claro. - Guarde imágenes VH-IVUS y cine IVUS en formato DICOM para analizarlas sin conexión.
- Segmentación y procesamiento de imágenes
- Abra archivos DICOM con el visor, haga doble clic en el nombre de la secuencia correspondiente para abrir la imagen y haga clic en Exportar > Exportar imágenes para guardar cada fotograma de cine IVUS o fotograma VH-IVUS como una imagen individual en formato BMP. Cada imagen BMP contiene 500 x 500 píxeles, tal y como indica el archivo DICOM original.
- Examine la imagen del cine IVUS fotograma a fotograma para encontrar los fotogramas consecutivos obtenidos en el sitio de la placa preseleccionado durante un ciclo cardíaco. Se generaron 26 fotogramas de cine IVUS durante un ciclo cardíaco para este sitio de placa de muestra.
- Examine todas las imágenes de VH-IVUS generadas para encontrar la imagen de VH-IVUS obtenida en el sitio de la placa dado. Las imágenes VH-IVUS utilizadas aquí se crearon utilizando un fotograma IVUS de los fotogramas IVUS del cine en un ciclo cardíaco.
- Segmente las imágenes de VH-IVUS y cine IVUS utilizando el software ImageJ para obtener los contornos de los límites de los vasos y los límites de los componentes de la placa (véase la Figura 1C).
- Seleccione la pestaña Línea recta > segmentada y delinee manualmente los contornos del lumen, el límite exterior del vaso coronario y los componentes de la placa en las imágenes de cine IVUS y VH-IVUS. Para la imagen de cine IVUS, solo segmente los contornos de la luz y el límite de los vasos externos, mientras que para la imagen de VH-IVUS, segmente los contornos de la luz, el límite de los vasos externos y los límites de los componentes de la placa.
- Para simplificar, mantenga solo los componentes lipídicos grandes para generar un modelo de elementos finitos e ignore los componentes lipídicos pequeños y aislados. Solo un lípido estaba presente en esta muestra de placa. Superponga los contornos delineados en las imágenes originales mediante Imagen > Superposición > pestaña Agregar selección .
- Vaya al menú Administrador de ROI para administrar contornos, ajustar propiedades y establecer los colores y el ancho de línea en los valores adecuados para una mejor visualización. Seleccione la pestaña Propiedades , establezca el color del trazo en un color diferente y rellene el ancho de línea en ancho. Aquí, establezca los colores de línea como verde, azul y rojo para los contornos de lúmenes, límites exteriores y lípidos, respectivamente, y el ancho de línea como 3.
- Suaviza los contornos con Editar > selección > Ajustar spline desde la barra de comandos después de seleccionar un contorno específico para obtener un contorno suave. Esta operación utiliza técnicas de ajuste de curva spline para suavizar automáticamente los contornos.
- Haga clic en Archivo > en la pestaña Coordenadas XY para guardar las coordenadas de punto de cada contorno, como el lumen, el límite exterior y >el componente de placa, en un archivo TXT independiente. Este archivo contiene los valores de las coordenadas x e y de los puntos que constituyen el contorno, con los píxeles como unidad.
- Registre el tamaño físico real de cada píxel en imágenes de cine IVUS y VH-IVUS (denotado como tamaño de píxel) desde el archivo DICOM. La distancia real de un píxel en los datos IVUS utilizados aquí es de 0,002 cm. Esta información se utilizaría para convertir las coordenadas de los puntos con el píxel como unidad a distancia real con cm como unidad.
- Procesamiento de datos de contornos
- Procesamiento de datos de contorno de Cine IVUS
- Lea archivos txt de los contornos de lúmenes de todas las imágenes de cine IVUS en un ciclo cardíaco con MATLAB.
- Multiplique todos los contornos de lúmenes por el tamaño de píxel para obtener el tamaño real de los contornos de lúmenes.
- Calcule las circunferencias de lúmenes para todos los contornos de lúmenes e identifique los marcos de IVUS con circunferencias de lúmenes máximas (Cmax) y mínimas (Cmin), que representan condiciones diastólicas y sistólicas, respectivamente.
- Procesamiento de datos de contorno VH-IVUS
- Lea archivos txt de los contornos de los componentes del lumen, el límite exterior y la placa de la imagen VH-IVUS con MATLAB.
- Multiplique todos los contornos por el tamaño de píxel para obtener el tamaño real de todos los contornos.
- Vuelva a dividir cada contorno en 100 puntos igualmente espaciados y realice un suavizado 2D para obtener nuevos datos de contorno VH-IVUS para reemplazar los antiguos.
- Procesamiento de datos de contorno de Cine IVUS
2. Modelo de elementos finitos
- Reconstrucción de la geometría de los vasos coronarios
- Cree una capa de contornos en el espacio tridimensional agregando el valor de la coordenada z para todos los puntos de los contornos de VH-IVUS, incluidos el lumen, el límite exterior y el lípido, y establezca z = 0 para todos los puntos (Figura 2).
- Cree otra capa de contornos agregando el valor de la coordenada z para todos los puntos de los contornos de VH-IVUS y restablezca z = 0,05 cm para todos los puntos.
NOTA: Estas dos capas de contornos reconstruyen la geometría de los vasos coronarios en 3D para el modelo de solo estructura de capa delgada agregando un espesor de capa fijo de 0,05 cm a los contornos de VH-IVUS (Figura 2).
- Generación de mallas de elementos finitos
- Cree dos contornos auxiliares interpolando linealmente los contornos de lúmenes y contornos de límite exterior con pesos 1/3 y 2/3 (Figura 3A) para cada capa.
- Divida el área del vaso en 8 partes circunferenciales y 3 partes radiales (ver Figura 3B) conectando el lumen/límite exterior al punto más cercano en el contorno lipídico (por ejemplo, puntos A y B en la Figura 3B) o dos contornos auxiliares con líneas radiales.
- Conecte todos los puntos entre capas con líneas rectas, formando una estructura 3D con volúmenes de 3 x 8 (Figura 3B). Divida cada volumen usando elementos hexaédricos para generar la malla de elementos finitos (Figura 3C) y diferentes grupos de materiales (Figura 3D).
- Realice un análisis de malla refinando la densidad de la malla en un 10 % hasta que los cambios en las soluciones < un 5 %.
- Definición de propiedades materiales
- Utilice un modelo de material anisotrópico de Mooney-Rivlin modificado para describir las propiedades del material de la pared de los vasos coronarios. Se asumió que los vasos coronarios y los componentes de la placa eran materiales hiperelásticos, anisotrópicos, casi incompresibles y homogéneos, y la función de densidad de energía de deformación del modelo de material anisotrópico modificado de Mooney-Rivlin es:
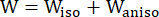 (1)
(1)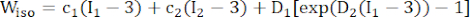 (2)
(2)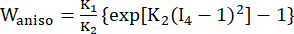 (3)
(3)
donde I1 e I2 son el primer y segundo invariantes del tensor de deformación de Cauchy-Green derecho C definido como c = [cij] = XTX, X = [Xij] = [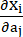 ], (Xi) fue la posición actual (aj) fue la posición original, I4 = cij(nc)i(nc)j, nc fue el vector unitario en la dirección circunferencial del recipiente. c1, c2, D1, D2, K1 y K2 fueron parámetros materiales específicos del paciente.
], (Xi) fue la posición actual (aj) fue la posición original, I4 = cij(nc)i(nc)j, nc fue el vector unitario en la dirección circunferencial del recipiente. c1, c2, D1, D2, K1 y K2 fueron parámetros materiales específicos del paciente. - Asigne los valores iniciales de los parámetros del material para un vaso coronario específico del paciente de acuerdo con los resultados de las pruebas biaxiales ex vivo, es decir, c1 = −1.312,9 kPa, c2 = 114,7 kPa, D1 = 629,7 kPa, D2 = 2,0, K1 = 35,9 kPa y K2 = 23,5 (Figura 4A-B)13,15.
- Asigne los parámetros del material para el componente de la placa, si está presente. Más específicamente, para los lípidos, c1 = 0,5 kPa, c2 = 0, D1 = 0,5 kPa y D2 = 1,5; para la calcificación se utilizó c1=920 kPa, c2=0, D1=360 kPa y D2=2,0 (Figura 4B)16.
NOTA: Se asumió que los componentes de la placa (lípidos y calcificación) eran hiperelásticos, isotrópicos y casi incompresibles, y sus propiedades mecánicas se describieron mediante un modelo de material isotrópico de Mooney-Rivlin con las funciones de densidad de energía de deformación dadas en la fórmula (2).
- Utilice un modelo de material anisotrópico de Mooney-Rivlin modificado para describir las propiedades del material de la pared de los vasos coronarios. Se asumió que los vasos coronarios y los componentes de la placa eran materiales hiperelásticos, anisotrópicos, casi incompresibles y homogéneos, y la función de densidad de energía de deformación del modelo de material anisotrópico modificado de Mooney-Rivlin es:
- Ecuaciones rectoras y establecimiento de condiciones de contorno
- Defina las ecuaciones de gobierno para el modelo de solo estructura de capa delgada, que incluye la ecuación de movimiento, la relación no lineal de deformación-desplazamiento de Cauchy-Green y el modelo de material de vasos coronarios11.
- Prescribir formas de onda de presión arterial específicas del paciente en la superficie del lumen para simular condiciones fisiológicas reales (Figura 4C). Para obtener formas de onda de presión arterial específicas del paciente, escale una forma de onda de presión aórtica típica con valores de presión sistólica y diastólica medidos con un manguito (Figura 4D).
3. Enfoque de actualización basado en modelos de elementos finitos para las propiedades del material de las arterias coronarias específicas del paciente
NOTA: El proceso iterativo para determinar las propiedades del material coronario específico del paciente se ilustra en la Figura 5.
- Determine la geometría sin carga correspondiente a la condición de presión cero como geometría inicial para el modelo computacional mediante la contracción de la geometría coronaria reconstruida a partir de la imagen VH-IVUS axialmente con una tasa de contracción fija del 95% y circunferencialmente con la contracción circunferencial (denotada como S) inicialmente establecida como 98%.
NOTA: Dado que la geometría coronaria reconstruida a partir de la imagen VH-IVUS se realizó en condiciones in vivo con presión arterial prescrita en la luz y estiramiento axial de los segmentos arteriales coronarios distal y proximal anclados, la geometría coronaria in vivo debe reducirse circunferencial y axialmente para obtener la geometría de presión cero. - Fije la tasa de contracción axial en 95% y actualice la contracción circunferencial durante los siguientes pasos.
- Defina la relación de material (denotada como k) para asignar las propiedades del material específico del paciente del vaso coronario como: es decir, c1 = k*(−1,312.9) kPa, c2 = k*114.7 kPa, D1 = k*629.7 kPa, K1 = k*35.9 kPa, y fije D2 = 2.0 y K2 = 23.5.
NOTA: Dado que solo se obtuvieron dos puntos de datos (circunferencias lumínicas mínimas y máximas correspondientes a las presiones diastólica y sistólica) para determinar los parámetros desconocidos (tasa de contracción circunferencial S y parámetros del material del modelo de Mooney-Rivlin), redujimos el número de parámetros desconocidos asumiendo que las propiedades del material específico del paciente in vivo del vaso coronario eran proporcionales a la estimación inicial con la relación de material denotada como k: es decir, c1 = k*(−1.312,9) kPa, c2 = k*114,7 kPa, D1 = k*629,7 kPa, K1 = k*35,9 kPa, mientras que D2 = 2,0 y K2 = 23,5 fueron fijos. - Actualice el valor k establecido a un valor inicial k de 1 junto con la tasa de contracción circunferencial S durante el siguiente procedimiento iterativo.
- Ejecute software para resolver el modelo computacional y obtener los resultados numéricos.
- Escriba todos los comandos para crear el modelo de solo estructura de capa fina en un archivo por lotes (archivo complementario 1) mediante MATLAB.
- Cargue este archivo por lotes mediante la interfaz de usuario avanzada (AUI) para generar el modelo (Figura 6A). Resuelva el modelo de solo estructura de capa delgada haciendo clic en Archivo de datos/Solución y guárdelo como un archivo .dat (Figura 6C). Simular tres ciclos cardíacos y adoptar la solución en el último ciclo para presentar resultados numéricos.
- Exporte los resultados de las coordenadas del nodo a un archivo txt navegando por Lista > Lista de valores > Zona y seleccionando POSICIÓN X, POSICIÓN Y y POSICIÓN Z en Variables para enumerar en Coordenada. Haga clic en Aplicar y exportar para exportar los resultados de las coordenadas.
- Guarde los datos de contorno de lúmenes correspondientes a las condiciones de presión diastólica y sistólica en archivos de .txt para los cálculos de la circunferencia de lúmenes.
- Compare las circunferencias de lúmenes calculadas por el modelo FE (modelo de estructura de capa de corte fino solamente) en condiciones de presión diastólica con datos in vivo de IVUS (Cmin) y verifique si el error relativo fue <1%. Si se cumplió la condición, vaya al siguiente paso o, de lo contrario, actualice la relación de material k utilizando el método secante y vaya al paso 3.3 para volver a ejecutar17,18.
NOTA: En la primera iterativa, se utilizó el método de Newton para actualizar la proporción de material en lugar del método secante. - Comparar las circunferencias lumínicas calculadas por el modelo FE en condiciones de presión sistólica con los datos de IVUS cine in vivo (Cmax) y comprobar si el error relativo fue del <1%. En caso afirmativo, detenga el procedimiento iterativo o, de lo contrario, actualice la tasa de contracción circunferencial S y redirija al paso 3.4 para volver a ejecutarlo.
NOTA: En la primera iterativa, se utilizó el método de Newton para actualizar la tasa de contracción circunferencial en lugar del método secante. - Registre los valores óptimos de S y k y calcule los parámetros de material correspondientes del modelo de material de Mooney-Rivlin.
- Trazar las curvas circunferencial y axial de la relación tensión-estiramiento del vaso coronario (Figura 7), que se pueden derivar de la siguiente manera:
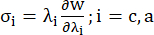 (4)
(4)
donde σ representa la tensión de Cauchy, λ representa la relación de estiramiento, i = c, a representa las direcciones circunferencial y axial.- Para dibujar una curva de material en una dirección determinada, fije la relación de estiramiento en la otra dirección en 1. Calcule el módulo de Young efectivo en la circunferencia y el axial (etiquetados como YMc e YMa, respectivamente) como la pendiente de la función de escala de la curva del material en el intervalo de la relación de estiramiento [1.0, 1.1] para reflejar la rigidez general del material de la arteria coronaria13:
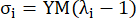 (5)
(5)
- Para dibujar una curva de material en una dirección determinada, fije la relación de estiramiento en la otra dirección en 1. Calcule el módulo de Young efectivo en la circunferencia y el axial (etiquetados como YMc e YMa, respectivamente) como la pendiente de la función de escala de la curva del material en el intervalo de la relación de estiramiento [1.0, 1.1] para reflejar la rigidez general del material de la arteria coronaria13:
- Extraiga las distribuciones de tensión/deformación de la placa en cualquier momento y registre la distribución de los ganglios y los valores máximos de tensión durante las fases sistólica y diastólica (Figura 8).
Resultados
Describimos en detalle el método FEMBUA, que permite un análisis rápido del material de la placa y del estrés de las placas coronarias después de la obtención de imágenes de IVUS en tiempo real y puede determinar las propiedades del material in vivo y los resultados biomecánicos de las placas. En la Tabla 1 se presentan los parámetros materiales in vivo del modelo de material de Mooney-Rivlin para este vaso coronario. Los resultados de la simul...
Discusión
Pasos críticos en el protocolo
El paso más crítico en el enfoque de actualización basado en modelos de elementos finitos se encuentra en el procedimiento iterativo. En este enfoque, el modelo de elementos finitos debe recuperar con precisión el movimiento de los vasos coronarios en la sección transversal vascular a partir de imágenes in vivo de cine IVUS. Para ello, en este estudio se adoptó la minimización de la diferencia de circunferencia lumínic...
Divulgaciones
Los autores declaran no tener ningún conflicto de intereses.
Agradecimientos
Esta investigación fue financiada en parte por el Proyecto de Ciencia y Tecnología de la Salud Médica de la Provincia de Shandong (No. 202425020256 y 202403010254), las subvenciones de la Fundación Nacional de Ciencias Naturales de China 11972117 y 11802060, la Fundación de Ciencias Naturales de la Provincia de Jiangsu bajo la subvención número BK20180352 y la Fundación de Ciencias Naturales de la Provincia de Shandong bajo la subvención número ZR2024QA110.
Materiales
| Name | Company | Catalog Number | Comments |
| Bee DICOM Viewer | SinoUnion Healthcare Inc. | Version 3.5.1 | A DICOM image reader software |
| ADINA | Adina R & D | Version 9.0 | Finite element solver |
| ImageJ | National Institutes of Health | Segmented IVUS contours | |
| MATLAB | MathWorks | Version R2018a | Commercial programming platform |
| Volcano s5 imaging system | Volcano Company | Intravascular ultrasound imaging system |
Referencias
- Roth, G. A., et al. Global burden of cardiovascular diseases and risk factors, 1990-2019: update from the GBD 2019 study. J Am Coll Cardiol. 76 (25), 2982-3021 (2020).
- Kanwar, S. S., et al. Acute coronary syndromes without coronary plaque rupture. Nat Rev Cardiol. 13 (5), 257-265 (2016).
- Milzi, A., et al. Coronary plaque composition influences biomechanical stress and predicts plaque rupture in a morpho-mechanic OCT analysis. Elife. 10, e64020 (2021).
- Stefanati, M., et al. Effect of variability of mechanical properties on the predictive capabilities of vulnerable coronary plaques. Comput Methods Programs Biomed. 254, 108271 (2024).
- Laurent, S., et al. Expert consensus document on arterial stiffness: methodological issues and clinical applications. Eur Heart J. 27 (21), 2588-2605 (2006).
- Daisuke, K., et al. Coronary plaque phenotype associated with positive remodeling. J Cardiovasc Comput Tomogr. 18 (4), 401-407 (2024).
- Macrae, R. A., Miller, K., Doyle, B. J. Methods in mechanical testing of arterial tissue: A review. Strain. 52, 380-399 (2016).
- Hayashi, K. Experimental approaches on measuring the mechanical properties and constitutive laws of arterial walls. J Biomech Eng. 115 (4B), 481-488 (1993).
- Sacks, M. S., Sun, W. Multiaxial mechanical behavior of biological materials. Annu Rev Biomed Eng. 5, 251-284 (2003).
- Charis, C., et al. Impact of combined plaque structural stress and wall shear stress on coronary plaque progression, regression, and changes in composition. Eur Heart J. 40 (18), 1411-1422 (2019).
- Wang, L., et al. Quantifying patient-specific in vivo coronary plaque material properties for accurate stress/strain calculations: An IVUS-based multi-patient study. Front Physiol. 12, 721195 (2021).
- Guo, X. Y., et al. Quantify patient-specific coronary material property and its impact on stress/strain calculations using in vivo IVUS data and 3D FSI models: a pilot study. Biomech Model Mechanobiol. 16 (1), 333-344 (2017).
- Wang, L., et al. Quantification of patient-specific coronary material properties and their correlations with plaque morphological characteristics: An in vivo IVUS study. Int J Cardiol. 371, 21-27 (2023).
- Lu, W., et al. Accurate identification of potential critical coronary lesions for the reduction of risk of cardiovascular events: study protocol for a randomized, open-label, active-controlled multi-center trial. Clin Trial Degenerat Dis. 3 (3), 106-110 (2018).
- Lv, R., et al. Using optical coherence tomography and intravascular ultrasound imaging to quantify coronary plaque cap stress/strain and progression: A follow-up study using 3D thin-layer models. Front Bioeng Biotechnol. 9, 713525 (2021).
- Camasao, D. B., Mantovani, D. The mechanical characterization of blood vessels and their substitutes in the continuous quest for physiological-relevant performances. A critical review. Mater Today Bio. 10, 100106 (2021).
- Holistic Numerical Methods Institute at University of South Florida. . Secant Method. , (2003).
- Barnes, J. An algorithm for solving nonlinear equations based on the secant method. Comp J. 8 (8), 66-72 (1965).
- Liu, M., Liang, L., Sun, W. A new inverse method for estimation of in vivo mechanical properties of the aortic wall. J Mech Behav Biomed Mater. 72, 148-158 (2017).
- Yu, H., et al. Patient-specific in vivo right ventricle material parameter estimation for patients with tetralogy of Fallot using MRI-based models with different zero-load diastole and systole morphologies. Int J Cardiol. 276, 93-99 (2019).
- Meuwissen, M. H. H., Oomens, C. W. J., Baaijens, F. P. T., Petterson, R., Janssen, J. D. Determination of the elasto-plastic properties of aluminium using a mixed numerical-experimental method. J Mater Process Technol. 75, 204-211 (1998).
- Davis, F. M., Luo, Y., Avril, S., Duprey, A., Lu, J. Local mechanical properties of human ascending thoracic aneurysms. J Mech Behav Biomed Mater. 61, 235-249 (2016).
- Fan, L., Wang, H., Kassab, G. S., Lee, L. C. Review of cardiac-coronary interaction and insights from mathematical modeling. WIREs Mech Dis. 16 (3), e1642 (2024).
- Andreas, W., et al. A finite element updating approach for identification of the anisotropic hyperelastic properties of normal and diseased aortic walls from 4D ultrasound strain imaging. J Mech Behav Biomed Mater. 58, 122-138 (2016).
- Liu, M., et al. Identification of in vivo nonlinear anisotropic mechanical properties of ascending thoracic aortic aneurysm from patient-specific CT scans. Sci Rep. 9, 12983 (2019).
- Trabelsi, O., Duprey, A., Favre, J. P., Avril, S. Predictive models with patient specific material properties for the biomechanical behavior of ascending thoracic aneurysms. Ann Biomed Eng. 44, 84-98 (2016).
- Cosentino, F., et al. On the role of material properties in ascending thoracic aortic aneurysms. Comput Biol Med. 109, 70-78 (2019).
- Krauz, K., et al. The role of epicardial adipose tissue in acute coronary syndromes, post-infarct remodeling and cardiac regeneration. Int J Mol Sci. 25 (7), 3583 (2024).
- McCracken, I. R., Smart, N. Control of coronary vascular cell fate in development and regeneration. Semin Cell Dev Biol. 155 (Pt C), 50-61 (2024).
- Holzapfel, G. A., et al. Determination of layer-specific mechanical properties of human coronary arteries with nonatherosclerotic intimal thickening and related constitutive modeling. Am J Physiol Heart Circ Physiol. 289 (5), H2048-H2058 (2005).
- Han, Y., et al. Ventricle stress/strain comparisons between Tertalogy of Fallot patients and healthy using models with different zero-load diastole and systole morphologies. PLoS One. 14 (8), e0220328 (2019).
- Ryo, K., et al. Role of the low-density lipoprotein-cholesterol/high-density lipoprotein-cholesterol ratio in predicting serial changes in the lipid component of coronary plaque. Circ J. 81 (10), 1439-1446 (2017).
- Thomas, T. W., et al. In vivo characterization and quantification of atherosclerotic carotid plaque components with multidetector computed tomography and histopathological correlation. Arterioscler Thromb Vasc Biol. 26 (10), 2366-2372 (2006).
- Masanori, K., et al. In vivo quantitative tissue characterization of human coronary arterial plaques by use of integrated backscatter intravascular ultrasound and comparison with angioscopic findings. Circulation. 105 (21), 2487-2492 (2002).
- Roach, M. R., Burton, A. C. The reason for the shape of the distensibility curves of arteries. Can J Biochem Physiol. 35, 681-690 (1957).
- Fung, Y. C., Liu, S. Q. Strain distribution in small blood vessel with zero-stress state taken into consideration. Am J Physiol. 262, 544-552 (1992).
- Ohayon, J., et al. Influence of residual stress/strain on the biomechanical stability of vulnerable coronary plaques: Potential impact for evaluating the risk of plaque rupture. Am J Physiol Heart Circ Physiol. 293, 1987-1996 (2007).
Reimpresiones y Permisos
Solicitar permiso para reutilizar el texto o las figuras de este JoVE artículos
Solicitar permisoExplorar más artículos
This article has been published
Video Coming Soon
ACERCA DE JoVE
Copyright © 2025 MyJoVE Corporation. Todos los derechos reservados