Resistencias en serie y en paralelo

Fuente: Yong P. Chen, PhD, Departamento de física & Astronomía, Facultad de Ciencias, Universidad de Purdue, West Lafayette, IN

Este experimento demuestra cómo se distribuye la corriente en resistencias conectadas en serie o en paralelo y así describe cómo calcular la resistencia total de «efectiva». Utilizando ley de Ohm, es posible convertir entre el voltaje y la corriente a través de una resistencia, si se conoce la resistencia.

Para dos resistencias conectadas en serie, (que significa que ellos están conectados uno después del otro), la misma corriente fluirá a través de ellos. Las tensiones se sumará hasta un "voltaje total" y, por tanto, la total "resistencia eficaz" es la suma de las dos resistencias. Esto a veces se llama un "divisor de tensión" porque la tensión total se divide entre las dos resistencias en proporción a sus resistencias individuales.

Para dos resistencias conectadas en paralelo, (que significa que ambos están conectados entre dos terminales compartidos), la corriente se divide entre los dos mientras que comparten el mismo voltaje. En este caso, el recíproco de la resistencia total efectiva será igual a la suma de los recíprocos de las dos resistencias.

Serie y paralelo resistores son un componente clave para la mayoría de circuitos e influyen en cómo la electricidad se utiliza en la mayoría de las aplicaciones.

La corriente eléctrica que fluye a través de un "dispositivo" (como un resistor de resistencia R) se define como la cantidad de carga Q que fluye a través del dispositivo por unidad de tiempo:

(Ecuación 1)

La corriente a través de un resistor (con resistencia R) se relaciona con la caída de voltaje V en la resistencia por ley de Ohm:

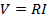(Ecuación 2)

Resistencias en serie:

Para dos resistencias (R₁ y R₂) conectadas en serie (figura 1), una continuidad actual significa que la corriente a través de R₁ es igual a la corriente a través del R₂, que es igual a la corriente a través de dos resistencias. Esto da:

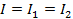(Ecuación 3)

Debido a la caída de voltaje a través de un dispositivo representa la diferencia de potencial entre los dos "terminales", la caída de tensión total V a través de ambas resistencias es la suma de las caídas de tensión individuales en cada resistencia:

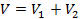(Ecuación 4)

Así, con la ley de Ohm, la caída de tensión total es igual a la resistencia eficaz, o la suma de R1 y R₂, veces la corriente:

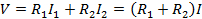(Ecuación 5)

Por lo tanto, la resistencia total o «efectiva» R de la combinación de toda la serie es igual a V / I. Así, la eficaz resistencia de resistores en serie es igual a la suma de las resistencias individuales. Es decir

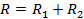(Ecuación 6)

Esto se puede generalizar también a una combinación de la serie de resistencias múltiples. Por ejemplo, si una resistencia grande se conecta en serie con una resistencia muy pequeña, la resistencia total será principalmente determinada por la resistencia grande.

Además, la corriente total I es igual a la caída de tensión total V dividida por la resistencia efectiva o la suma de las dos resistencias:

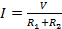(Ecuación 7)

Así, las caídas de tensión individuales (V₁ y V₂) pueden estar relacionado con la caída de tensión total V como:

(Ecuación 8)

y,

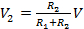(Ecuación 9)

Esta relación describe la "división de tensión", o cómo la tensión se divide entre las resistencias de dos series proporcionales a la resistencia.

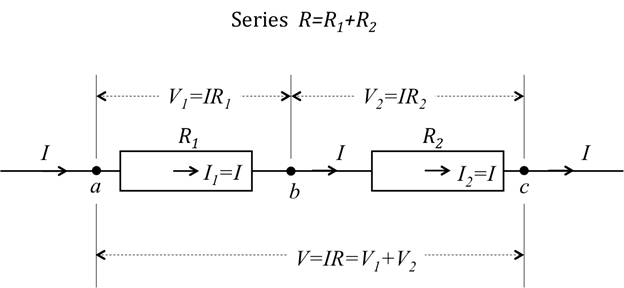
Figura 1: Diagrama que muestra dos resistores conectan en serie.

Resistencias en paralelo:

Si las dos resistencias en su lugar se conectan en paralelo, como se muestra en la figura 2, que comparten la misma caída de tensión V, pero la corriente total que está dividido entre ellos:

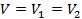(Ecuación 10)

y,

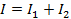(Ecuación 11)

Por lo tanto:

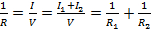(Ecuación 12)

que también significa que la resistencia efectiva, R, es igual a la "suma de productos" de las dos resistencias paralelas, o:

(Ecuación 13)

Cualquier resistencia es también un conductor, y la conductancia G de una resistencia R se define como el inverso de la resistencia:

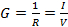(Ecuación 14)

donde la segunda igualdad es debido a la ley de Ohm (ecuación 2).

Entonces para resistencias paralelo:

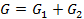(Ecuación 15)

es decir, "paralelo conductancias añadir".

Si una resistencia grande está conectada en paralelo con una resistencia muy pequeña, la resistencia total está determinada principalmente por la pequeña resistencia, que tiene la gran conductancia.

Para una conexión en paralelo, la corriente se dividirá en proporción a la conductancia

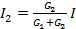, y (ecuación 16)

que también significa,

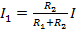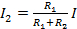, y (ecuación 17)

(nota sin embargo, el numerador es la otra resistencia).

Para todos estos ejemplos, es importante tener en cuenta que se supone que los cables de conexión de las resistencias tienen resistencias insignificante pequeñas comparado con R₁ y R₂. Si no, los cables se deben modelar como resistencias conectadas en serie para R₁ y R₂y añadir sus resistencias para formar parte de R₁ y R₂.

Figura 2: Diagrama que muestra dos resistores conectan en paralelo.

1. práctica en generar y medir corriente, voltaje y resistencia

1. Obtener una fuente de corriente, una fuente de tensión y dos multímetros pueden medir voltaje, corriente, y resistencia.
2. Obtener dos resistencias de 100-Ω y dos resistencias de 10-Ω.
3. Obtener un protoboard, que es una plataforma conveniente para conectar y organizar elementos de circuito diferente. La protoboard tiene muchos grupos de pines. Los pernos de cada grupo están conectados juntos en la parte posterior de la Junta, y los cables enchufados en el mismo grupo están en cortocircuito juntos. Un cable enchufado en el mismo grupo de pines como un terminal de un elemento de circuito está conectado a ese terminal. Diferentes terminales de un elemento de circuito no pretende estar en corto circuito deben conectarse a grupos de pines diferentes. En el siguiente, la acción de dos terminales de conexión significa que enchufarlos en el mismo grupo de pin (en las figuras, distintivo nodos etiquetados "a", "b" y "c" representan grupos de pin distintivo en la protoboard). Ello, siempre que dichos terminales se hacen de alambres que pueden colocarse convenientemente en un agujero. De lo contrario, es posible utilizar cables, enchufes de plátano y pinzas para hacer las conexiones eléctricas (por ejemplo, desde una terminal en el instrumento a una pierna de pin expuesta en la protoboard).
4. Conecte el terminal de salida de la fuente actual a un terminal de la resistencia de 100-Ω y luego conecte la otra terminal de la resistencia a la otra terminal de la fuente actual.
5. Generar 1 mA de corriente a través del resistor.
6. Seleccionar la medida de voltaje o voltímetro del multímetro y conectar los dos terminales del multímetro a los dos terminales de la resistencia. Medida de la caída de tensión cruzan la resistencia.
7. Una lectura positiva significa que el potencial en el terminal positivo del multímetro es mayor que en el polo negativo. Utilizar la lectura de tensión para verificar la relación de ley de Ohm (figura 3).
8. A continuación, conecte un terminal de una fuente de tensión a un terminal de la resistencia y conecte la otra terminal de la resistencia a la otra terminal de la fuente de tensión. Producir un 10 V tensión en la resistencia de 100-Ω.
9. Utilice el multímetro en el modo amperímetro o medición de corriente y conecte las puntas de prueba en serie con la resistencia. Medir la corriente a través del resistor.
   1. Una lectura positiva significa que la corriente eléctrica fluye desde el terminal positivo del multímetro al borne negativo. Luego, verificar la ley de Ohm (figura 4).
   2. Tenga en cuenta que el multímetro debe estar en serie con una resistencia para medir la corriente (amperímetro), pero tiene que ser en paralelo con una resistencia para medir la caída de tensión (voltímetro). En estas mediciones, se asume que la resistencia "interna" del amperímetro es muy pequeña pero que del voltímetro es muy grande. Si esto no es rigurosamente cierto entonces la corriente o el voltaje medido por el medidor sería diferente del valor antes de la conexión del medidor.
10. Por último, medir la resistencia con el multímetro (figura 5) directamente seleccionando el modo de medición de resistencia. Conectar los dos terminales del metro con los dos terminales de la resistencia y la resistencia de leer. Confirmar que la resistencia tiene sentido basado en las mediciones de corriente y tensión anteriores.

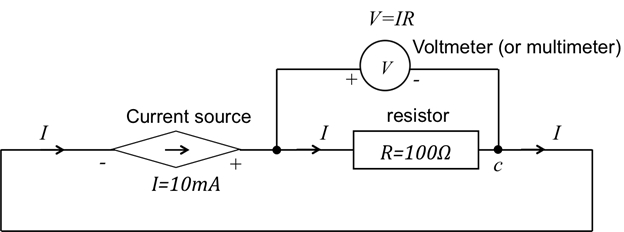
Figura 3: esquema de una corriente por el resistor R de abastecimiento y medición de tensión.

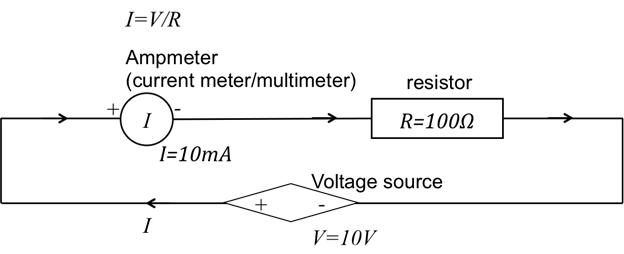
Figura 4: diagrama del circuito de abastecimiento de un voltaje en el resistor R y medición actual.

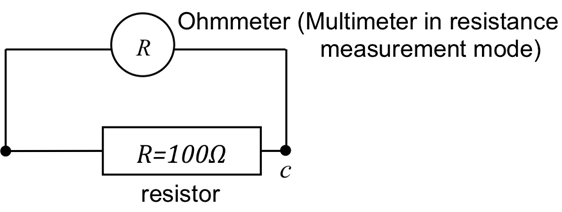
Figura 5: conexión de un multímetro para medir resistencia de un resistor.

2. resistores en serie

1. Conectar dos resistencias de 100-Ω en serie (ver figura 1). En el protoboard, esto significa conectar los dos extremos de la primera resistencia en dos grupos de diferentes pin (no pone en cortocircuito), dice grupo un y b y conectar los dos extremos de la resistencia de segunda en pin grupos b y c (c es aún otro grupo de pin no pone en cortocircuito para un y b).
   1. Conectar una corriente común de 10 mA a través de ambos resistores utilizando una fuente de corriente como se describe en el paso 1.4.
   2. Con un multímetro en modo de voltímetro, medir la caída de tensión en cada resistencia. A continuación, confirme los valores de resistencia de R₁ y R₂ usando ley de Ohm.
   3. Ahora use el voltímetro para medir el voltaje V a través de la combinación de toda la serie (entre los puntos a y c en la figura 1) y obtener la resistencia en serie total.
   4. Introduzca los valores de resistencia, como se muestra en la tabla 1.
   5. Desconecte las fuentes de energía y metros, luego utilizar una fuente de voltaje para proporcionar un total de 10 V a través de dos resistencias (entre los puntos a y c).
   6. Usar un multimetro en modo amperímetro para medir la corriente (I₁) entrar en R₁y la corriente (I₂) entrar en R₂.
   7. Verificar que₁ es igual₂ (o aproximadamente igual, cualquier pequeña diferencia podría deberse a configuraciones ligeramente diferentes, incluyendo las resistencias de alambre que cambió un poco).
2. Repita el procedimiento en el paso 2.1 para dos resistores de 10-Ω en serie y medir la resistencia con el multímetro.
3. Repita el procedimiento en el paso 2.1 para una resistencia de 100-Ω en serie con el resistor de 10-una Ω y repita las mediciones de resistencia.

3. resistencias en paralelo

1. Conectar dos resistencias de 100-Ω en paralelo (ver figura 2). En el protoboard, conecte los dos extremos de cada resistencia en dos grupos de pin, decir a y b.
   1. Fuente común caída de tensión de V = 10 V mediante una fuente de tensión.
   2. Utilice un multímetro para medir la corriente I₁ entrada R₁, confirmando así que R₁ = V / I₁. Entonces, medir₂ en R₂, confirmando así que R₂ = V / I₂.
   3. Ahora ponga el amperímetro frente a la combinación paralelo (antes del punto a en figura 2) y obtener la resistencia total R = V / I.
2. Repita lo anterior en el paso 3.1 para dos resistores de 10-Ω en paralelo y una resistencia de 100-Ω en paralelo con una resistencia de 10 Ω.

4. LED en serie y conexión en paralelo

1. Obtener dos pequeñas fuentes de luz LED, que pueden ser tratadas como dos resistencias.
2. Conecte la fuente V 1 para LED de potencia 1 (conexión similar como paso 1.5) y observe su brillo.
3. Ahora conectar los LEDs en paralelo entre la fuente V 1 (conexión similar como en el paso 3.1) y observar su brillo.
4. Ahora conectar los dos LEDs en serie y entre la fuente V 1 (conexión similar como paso 2.1.5) y observar su brillo otra vez.

Resultados representativos previstos por el procedimiento anterior se enumeran en la tabla 1 para resistencias en serie y en la tabla 2 para resistencias en paralelo.

Según los resultados en la tabla 1, la resistencia total R medida obedece ecuación 6, donde las resistencias de los componentes en serie añadir para dar la resistencia total. Los resultados en la tabla 2 muestran que la resistencia total de resistores en paralelo sigue ecuación 12 (o ecuación 13), donde añadir los recíprocos (es decir, conductancias) de las resistencias en paralelo para dar la resistencia total efectiva.

Cuando usar LEDs en lugar de resistencias, está claro que los LEDs conectan en paralelo tienen brillo similar al solo LED conectado a la misma fuente de voltaje. Esto es porque los LEDs son alimentados por la tensión, y los conectan en paralelo comparten la misma fuente de voltaje (1 V en este caso). Por lo tanto, la configuración no afecta el funcionamiento de cada LED. En contraste, los LEDs conectados en serie son más dévil que la LED solo. Esto es porque los dos LEDs en serie cada uno reciben sólo 0,5 V, la tensión se reparte entre ellos.

R1	R2	Rseries
100 Ω	100 Ω	200 Ω
10 Ω	10 Ω	20 Ω
100 Ω	10 Ω	110 Ω

Tabla 1: Los datos recogidos para la serie de dos resistencias R₁ y R₂ y la resistencia efectiva total R = R_serie.

R1	R2	Paralelo de R
100 Ω	100 Ω	50 Ω
10 Ω	10 Ω	5 Ω
100 Ω	10 Ω	9.1 Ω

Tabla 2. Los datos recogidos por dos paralelo resistencias R₁ y R₂ y la resistencia efectiva total R = R_paralelo.

En este experimento, hemos repasado cómo utilizar tensión y fuentes de corriente y multímetro (voltímetro, amperímetro de corriente, ohmetro) para verificar la actual Ley de continuidad y ley de Ohm. También demostramos cómo añade resistencia en serie, y cómo agrega conductancia en paralelo.

Conexiones paralelo y serie son comunes en muchas aplicaciones de circuitos. Por ejemplo, para utilizar una fuente de voltaje V como una fuente de corriente para algún dispositivo con una resistencia R₁, conecte una mucha resistencia fija mayor R₂ con la fuente de tensión y el dispositivo R₁. Entonces, la corriente a través de R₁ es aproximadamente V/R_2.

Cuando cualquier aparato eléctrico o equipo se conecta a un tomacorriente de 110 V en la pared, la conexión se realiza en paralelo con otros instrumentos que pueden haber ya sido enchufado. Todos ellos comparten el voltaje común de 110 V y cada uno debe funcionar sin afectar a otras personas-dentro de un cierto rango de condiciones de operación.

El autor del experimento agradece la ayuda de Gary Hudson para la preparación de material y Chuanhsun Li para la demostración de los pasos en el video.