Characterizing Dissipative Elastic Metamaterials Produced by Additive Manufacturing
In This Article
Summary
Additively manufactured polymers have been widely used for producing elastic metamaterials. The viscoelastic behavior of these polymers at ultrasonic frequencies remains, however, poorly studied. This study reports a protocol to estimate the viscoelastic properties of 3D-printed polymers and show how to use them to analyze the metamaterial dynamics.
Abstract
Viscoelastic behavior can be beneficial in enhancing the unprecedented dynamics of polymer metamaterials or, in contrast, negatively impacting their wave control mechanisms. It is, therefore, crucial to properly characterize the viscoelastic properties of a polymer metamaterial at its working frequencies to understand viscoelastic effects. However, the viscoelasticity of polymers is a complex phenomenon, and the data on storage and loss moduli at ultrasonic frequencies are extremely limited, especially for additively manufactured polymers. This work presents a protocol to experimentally characterize the viscoelastic properties of additively manufactured polymers and to use them in the numerical analysis of polymer metamaterials. Specifically, the protocol includes the description of the manufacturing process, experimental procedures to measure the thermal, viscoelastic, and mechanical properties of additively manufactured polymers, and an approach to use these properties in finite-element simulations of the metamaterial dynamics. The numerical results are validated in ultrasonic transmission tests. To exemplify the protocol, the analysis is focused on acrylonitrile butadiene styrene (ABS) and aims at characterizing the dynamic behavior of a simple metamaterial made from it by using fused deposition modeling (FDM) three-dimensional (3D) printing. The proposed protocol will be helpful for many researchers to estimate viscous losses in 3D-printed polymer elastic metamaterials that will improve the understanding of material-property relations for viscoelastic metamaterials and eventually stimulate the use of 3D-printed polymer metamaterial parts in various applications.
Introduction
Polymers reveal viscoelastic response to a greater or smaller extent. This means that in addition to elastic behavior described by elastic (storage) moduli, they have viscous (loss) components. Viscous losses cause delay in the development of stress under applied strain and vice versa. Under dynamic excitation, out-of-phase stress components are dissipated through heat, thus reducing the energy of acoustic waves propagating in a viscoelastic medium. This phenomenon is referred to as viscous damping.
Viscosity originates at a molecular level due to relative motions or local rotations of bonds in polymer chains and, thus, is governed by the chemical composition, structure, and connections of polymer chains. Molecular mobility depends on temperature and deformation rate, resulting in temperature- and time-driven behavior of viscoelastic materials. All this makes viscoelasticity an inherently complex phenomenon that has a unique signature for each material. One feasible way to approximate such behavior implies modeling a viscoelastic material as a mechanical system composed of (Hookean) springs and (Newtonian) dashpots1. Although this approach fully neglects the molecular structure of a material and all the complexity of a real relaxation process, it can provide adequate results for hard polymers with comparatively low viscous losses2.
The key to obtaining an adequate mechanical model is tuning the parameters of the springs and dashpots to experimental data for the storage and loss moduli of a viscoelastic polymer3,4,5,6,7,8. This work describes a set of methods to determine the viscoelastic moduli of additively manufactured polymers and to use them in characterizing the dynamics of elastic metamaterials. By this, we aim to bridge the gap between material properties and the structure-driven dynamics of metamaterials, enabling a more robust and reliable design of metamaterials for target working frequencies.
Elastic metamaterials are a class of engineered, often periodically structured materials that can manipulate acoustic waves in solids in an unusual yet controllable way9. The wave manipulation is mainly implemented by tailoring bandgaps - the frequency ranges in which wave propagation is prohibited4. The unique dynamics of elastic metamaterials are governed by a fine-tuned architecture represented by complex-shaped unit cells, especially for three-dimensional configurations. Such structural complexity can often be realized only using additive manufacturing which makes viscoelasticity analysis especially relevant for additively manufactured elastic metamaterials. Most current studies, however, have used oversimplified models of viscosity, such as the Maxwell10,11 or Kelvin-Voigt model11. Because these models cannot describe any real viscoelastic material2, the conclusions derived by using them cannot be considered reliable. Therefore, there is a burning need for more realistic models replicating viscoelastic material properties at ultrasonic frequencies. Several studies have addressed this need6,8,12 and reported serious limitations of commercial finite element solvers due to high13 computational load, especially when dealing with complex geometries and/or high frequencies14 and the restriction on considering the relaxation of a single modulus (in reality, both moduli of an isotropic medium under relaxation). Another analysis method, e.g., plane wave expansion, can reduce the computational burden15, but requires an analytical description of the scatterer geometry, limiting its applicability. The extended plane wave expansion approach16,17 addresses this limitation but adds computational complexity. The Bloch wave expansion18 and transfer matrix methods19 can only consider periodic structures of finite dimensions, which can be described analytically. The spectral element approach20,21 offers computational efficiency, but its applicability is limited to very low frequencies below the first bandgap. Thus, in addition to the lack of experimental data for storage and loss moduli at room temperature and high frequencies (above 100 Hz), which are common work conditions for elastic metamaterials20,22,23,24, the analysis of their dynamics remains challenging. This work aims to fill in these gaps by summarizing the experimental (and numerical) techniques for the characterization of additively manufactured viscoelastic polymers and elastic metamaterials made of them.
This approach is illustrated by analyzing a simple one dimensional (1D) continuous analog of a periodic mass-spring model made of commonly used acrylonitrile butadiene styrene (ABS) polymer and produced by a fused-deposition modeling (FDM) 3D-printing (Section 1), for which one can experimentally determine the decomposition and glass transition temperatures (Section 2) and derive the master curves for storage and loss moduli at reference room temperature (Section 3). In addition, the quasi-static mechanical moduli can be estimated in tensile tests (Section 4) and linked to their dynamic counterparts. Next, the numerical method to model the dynamic characteristics of a metamaterial is described (Section 5), and the obtained numerical results are validated experimentally in transmission experiments (Section 6). Finally, the applicability and limitations of the proposed methods based on the findings are discussed.
Protocol
1. 3D printing procedure for polymer samples
NOTE: The 3D printing of polymer samples on an FDM 3D printer includes a preparatory phase, printing process, and post-processing.
- Preparation of the model
- Create a 3D model of a sample geometry in any software supporting computer-aided design (CAD) and export it as an STL, OBJ, or STEP file.
NOTE: For metamaterials, the common software is a commercial (COMSOL Multiphysics, Abaqus, SolidWorks, etc.) or open-source (Elmer, MSLattice, etc.) finite-element package or CAD (Grasshopper, Fusion 360, SketchUp, 3DMECMET, GrabCAD, etc.) software for complex geometries. - Open the exported file in a slicer to construct an actual model for 3D printing based on the generated digital model. Specify the print settings, such as the orientation of the sample (to reduce the need for support), print speed and temperature (governed by the choice of a filament), infill density for solid parts (100% for metamaterial samples), layer height, eventual support for hangover parts, etc.
NOTE: Specific values for these settings depend on the model of a 3D printer and can be found in corresponding manuals. - Store the sliced geometry and the specified settings in a G-code file sent to the 3D printer through a network connection or an external USB drive.
- Create a 3D model of a sample geometry in any software supporting computer-aided design (CAD) and export it as an STL, OBJ, or STEP file.
- Preparation of a 3D printer
- Before starting the 3D printing process, clean the print bed with alcohol and a microfiber cloth.
- Apply a layer of adhesive (e.g., hairspray, glue, or glass-bed adhesive) on the print bed area where the sample will be 3D printed.
- Upload a filament into a nozzle, according to a manual for the 3D printer, and ensure that it is extruded properly.
- Start the 3D printing process following the instructions for the 3D printer.
- 3D printing process and post-processing
- Ensure that the 3D printer reaches the specified value of bed temperature before starting the printing process.
- Once the 3D printing is finished, let the temperature of the print bed reduce to room temperature (RT) and carefully remove the 3D printed sample.
- Cut the support or brim layer out or wash away for a clean final structure.
2. Thermogravimetric analysis (TGA) and differential scanning calorimetry (DSC)
NOTE: The TGA and DSC techniques follow a similar protocol that includes sample loading, defining experimental parameters, and test conditions, which are followed by data processing.
- Sample loading
NOTE: Ensure that the sample is in powdered form or small pieces so that the total weight does not exceed 5 mg (about half the weight of a grain of table salt).- Open the TGA oven chamber door, position the aluminum/platinum sample pan on the balance pan, and tare the balance.
- Transfer the sample onto the sample pan cautiously using a spatula.
- Record the sample mass (typically 2-5 mg) and close the oven chamber door.
- Experimental parameters
- Define the specific experimental parameters, including temperature range, heating rate, and atmosphere (nitrogen gas).
- Specify additional parameters (e.g., time step, ramp rate) and start the experiment.
- Experimental tests
- TGA: Continuously monitor the sample mass while varying temperature or time and note variations in the weight, which might indicate processes like decomposition, oxidation, or desorption.
- DSC: Continuously evaluate the heat flow as a function of temperature or time and note any endothermic or exothermic peaks that potentially signify phase transitions, crystallization, melting, or chemical reactions.
- Data collection and analysis
- Export data as binary "ASCII" or MATLAB "mat" files for plotting using tools like OriginPro, MATLAB, etc.
- Examine the measured TGA curve for step changes that indicate transitions in the sample's mass loss behavior and are characterized by sudden shifts in the slope of the curve. Identify the temperature corresponding to a 5% mass loss of the sample as the decomposition temperature. The peaks of the derivative thermogravimetry (DTG) curve indicate the points of maximum rate of mass loss.
- In the analysis of the DSC curve, identify the inflection points characterized by changes in the curve's slope as they reflect changes in the heat flow rate associated with different phase transitions occurring within the sample. Locate the onset temperature of each inflection point, which represents the point on the temperature axis where the change in slope begins. For glass transition temperature (Tg) determination, the inflection point corresponds to the midpoint of the transition region where the curve deviates from the baseline.
NOTE: A well-defined baseline curve ensures proper calibration of the instrument. If the baseline is not flat, it could indicate the instability of an instrument, improper sample handling, or contamination. The sharpness of the curve indicates the homogeneity and purity of the sample. It is common to extract data from the second cycle of DSC experiments to avoid the influence of any impurity or residual stress within the sample on the results.
3. Dynamic mechanical analysis (DMA) for material characterization
NOTE: Characterizing the viscoelastic properties of a polymer with a dynamic mechanical analyzer involves securing a sample in one of the several test setups listed in Table 1. The protocol of the DMA experiment includes the following steps.
- Sample preparation
- Fabricate test samples of cuboidal shape using a hot press, molding, cutting, or 3D printing. Ensure that the sample edges are parallel and smooth. Use abrasive paper if needed. Avoid forming air bubbles in the material.
- Refer to Table 2 for the test sample dimensions for four test configurations.
NOTE: The following protocol focuses solely on the procedure for the single cantilever test configuration which suits well for 3D-printed (hard) polymers. A similar protocol applies to the other test configurations.
- Designing experiment
- Define the temperature range for the test, the glass transition temperature, and the melting temperature of the material (based on DSC).
NOTE: To ensure accurate results, avoid operating at temperatures that are 20 °C higher or lower than the glass transition point. - Choose a heating rate of 1-3 °C/min. Choose the lowest strain value for optimal outcomes. Typical displacements vary between 5 µm and 50 µm. Usually, a starting point of 10 µm is appropriate. Configure the parameters for the frequency sweep and the heating rate.
- Define the temperature range for the test, the glass transition temperature, and the melting temperature of the material (based on DSC).
- Calibration
- Choose the single-cantilever test configuration and disconnect the oven by removing the clamps located on the sidewalls.
- Adjust the fixed clamp to the necessary measuring length (according to the dimensions of the sample) by removing and reinstalling it on the DMA machine.
- Ensure that the screws on the movable clamp are securely tightened and immobile. Make sure that the clamp does not touch the thermocouple.
- Initiate the calibration process to guarantee that the force calculations do not include the weight of the measurement geometry. Perform calibration at every start of the machine or switch of a test configuration.
- Clamping the sample
- Loosen the screws of the stationery and adjustable clamps when the Park mode is activated. Parking refers to restricting the movement of the adjustable clamp to avoid damage to the instrument while clamping.
- Slide the test sample through one side and rest it on the threads of the clamps. Use a torque wrench to screw the adjustable clamps, followed by the stationary clamps, with just enough effort to hold the sample without additional support.
- Review the sample for any misalignment.
- To verify the adequacy of the sample clamping and the functionality of the procedure, initiate a manual oscillation. This exerts a variable force on the sample without recording the data.
NOTE: If the storage modulus of the sample remains below 0.1% (or the dynamic force below 5 N), then the technique and clamping are considered adequate.
- Performing the measurement
- Reinstall the oven by placing it over the test configuration and input the initial temperature manually. Open the liquid nitrogen valve in one complete revolution and wait at least 3 min after reaching the desired temperature.
- Start the measurements and follow them on a computer screen.
- After the measurements are finished and the oven temperature returns to ambient, close the nitrogen valve. Remove the oven and the sample, and do not reuse the sample for further testing.
- Data analysis
- Save the data, select the curves, and shift them to a reference temperature using appropriate shift factors to obtain a master curve at the reference temperature.
- Plot the specified mechanical properties (e.g., storage modulus, loss modulus, tan δ) versus frequency for the time-temperature superposition (TTS) curve. The horizontal axis usually depicts frequency on a logarithmic scale.
- Analyze the variations of the mechanical properties with frequency.
NOTE: Hard polymer materials often exhibit viscoelastic moduli that adhere to a power-law correlation with the frequency indicated by a slope change on a log-log plot. The intersection of loss and storage moduli curves signifies the crossover frequency, suggesting a shift in the predominant viscoelastic properties of a polymer. Within specific frequency ranges, the mechanical characteristics of the material may remain frequency-independent, i.e., a plateau zone where the material mostly behaves elastically. - Export data as binary "ASCII" or MATLAB "mat" files for plotting using tools like OriginPro, MATLAB, etc.
4. Tensile testing coupled with digital image correlation (DIC)
NOTE: This protocol is described for operating the Q400 DIC system (LIMESS Messtechnik & Software GmbH, Germany) using the software Istra4D.
- Sample preparation
- Fabricate a test sample, as per designation D638−14, using an additive manufacturing technique.
- Apply a speckle pattern using sprays or surface treatment to create a smooth surface suitable for the DIC analysis, ensuring an ideal speckle size of 3-5 pixels in diameter.
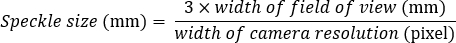
For example, if the width of the field of view is 80 mm and the camera resolution is 2000 pixels wide, the calculation would be:
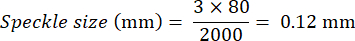
- Experimental setup
- Mount the specimen in the tensile testing machine properly by ensuring proper alignment and gripping to prevent slippage during testing.
- Connect the DIC hardware to the software.
- Set up high-resolution cameras to capture images of the specimen's surface. Ensure the cameras have a sufficient field of view to capture the entire region of interest.
- Configure appropriate lighting to ensure uniform illumination across the specimen's surface. Avoid shadows or glare that might affect image quality.
- Calibration
- Start a new calibration process and adjust the color palette to GrayMinMax.
- Select an appropriate lens and open the aperture completely. Adjust Exposure Time (e.g., 50 ms) to capture images with fewer red dots.
- Adjust focus and aperture to get minimum red dots on the surface of the test specimen.
- Choose a calibration and acquire calibration images, ensuring the plate is tilted in all directions.
- Save the calibration data.
- Experimental test
- Capture initial images of the specimen in its original state without any load.
- Begin applying a tensile load to the specimen at a controlled rate according to the testing standards.
- Simultaneously capture images of the specimen's surface at regular intervals or continuously throughout the testing process.
- Transfer captured images to a computer equipped with the DIC software for analysis. Use the software to correlate images between consecutive frames, tracking surface displacements and deformations.
- Analysis and post-processing
- Select the desired image series from the project explorer. Initiate a new analysis by clicking on New Evaluation and define a name for the analysis.
- Adjust the analysis parameters (facet size, grid spacing, etc.) in the Evaluation Settings tab. Set the Grid Spacing to approximately one-third of the Facet Size for optimal analysis accuracy.
- Use masks to define areas of interest or exclusion (Polygon 1 in Figure 6A) within the analysis. Validate the start point search in the Startpoints tab by clicking on Start. Ensure all steps are marked with a green half-circle for automatic assignment.
- Begin the analysis by navigating to the Control tab and clicking on Start. Monitor the analysis progress, ensuring all image steps are marked with a green full circle upon successful completion.
- Analyze the DIC results to calculate strain and displacement fields across the specimen's surface using the modules available in the software. Extract relevant mechanical characteristics such as stress-strain curves, Young's modulus, ultimate tensile strength, etc.
- Post-process the data using necessary techniques (e.g., filtering, smoothing) to enhance accuracy and readability.
- Interpret the results to conclude the material behavior under tensile loading conditions.
5. Finite element studies for wave dynamics in metamaterials
NOTE: Below is the description of the finite-element-based procedure for the transmission analysis of an elastic metamaterial using commercial finite-element software COMSOL Multiphysics.
- Model preparation
- Begin by using the Model Wizard to create a new model. Select the 3D space dimension and add the Solid Mechanics study. In the study window, choose the Frequency Domain study for transmission analysis.
- Define relevant parameters and assign values to them under the Global Definitions tab. Create the geometry of a metamaterial model using available tools. The model is typically composed of a set of interconnected unit cells.
- Right-click on components to access the Definitions tab, then select Probes and choose Boundary Probe. Assign a boundary on the model to this boundary probe where the transmission loss is to be calculated. Define the mathematical expression to estimate the ratio of transmitted wave energy to the input energy at this boundary probe as follows:
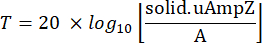
where T is the transmission ratio, A is the amplitude of excitation at the incident plane, and solid.uAmpZ is components of displacement at the output plane, along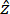 .
. - To avoid the generation of spurious reflected waves from the domain boundaries, define a perfectly matched layer (PML) by right-clicking on the Definitions tab and assigning PML properties to geometric blocks surrounding the metamaterial geometry. The PML size should be large enough to attenuate unwanted reflections, typically 2-6 times the wavelength of the incoming wave. Alternatively, to model the periodic extension of a medium, apply periodic boundary conditions at faces perpendicular to the periodicity direction and enable the Continuity feature.
- Assign material properties to the geometry by right-clicking on the Materials tab and adding materials from the library. Alternatively, select a blank material property that requires manual specification of required material properties.
- Under the Component tab, the default physics settings assign linear elastic material behavior to the analyzed geometry. To incorporate viscoelastic properties, right-click on the Linear Elastic Materials tab and select the viscoelasticity material model. The Generalized Maxwell Model is a suitable choice due to its ability to comply with experimental data obtained from DMA tests. Enter the deviatoric tensor obtained from the calculation based on DMA results.
- Right-click on the Prescribed Displacement tab and select a portion of the model to be dynamically excited from the Graphics window. Envisioning experimental validation of transmission results in a pitch-catch test with piezo elements, assign the amplitude of out-of-plane displacement at the expected position of a piezo element.
- Generate a suitable mesh for the analyzed model with the mesh element size obeying the rule that there must be at least 5-7 finite elements to resolve the smallest wavelength under consideration. Do this by defining the mesh manually or assigning physics-controlled mesh settings. The Swept mesh feature is more compatible with PML settings to define their absorbing behavior.
- Configuring the Solid Mechanics study parameters for a viscoelastic model
- For rheological simple polymers, temperature-induced effects on the viscoelastic properties of a polymer can be directly translated into a shift in the time scale by applying a shifting factor. Choose an appropriate shift function from the drop-down menu. Select None if the temperature effects are already considered in the DMA results to be used.
- Select an appropriate viscoelastic model, e.g., the Generalized Maxwell Model, a common choice for viscoelastic materials due to its ability to capture experimentally measured relaxation behavior. Enter the values for the deviatoric tensor based on calculations.
- One method to calculate the relaxation time (τ) from DMA results involves identifying the peak or maximum value in the loss modulus curve, which corresponds to the relaxation process in the material. Estimate the frequency (f) associated with this peak to calculate the relaxation time, τ = 1/(2πf).
- For the general procedure to estimate the parameters of the Generalized Maxwell model fitting experimental data, use the built-in fitting tool that can be found in the Parameter Estimation tab. Perform the fit with an optimization solver that allows the comparison of the current model prediction with the experimental data in real-time.
- Computing the study
- From the study library in the Add Study option, select Frequency Domain and enter the target frequency range. Define the number of intermediate frequencies in this frequency range.
- Compute the study by pressing the Compute button.
- Data analysis and processing
- After the computation is complete, right-click on the Results tab and select the 1D Plot Group function. Right-click on the created 1D plot group and choose Global from the options.
- In the Y-axis data tab of the Settings window, input the mathematical expression for transmission loss. Alternatively, enter the nickname assigned to the boundary probe in the previous steps.
- Choose the parameter for the x-axis from the drop-down menu in the X-axis data tab and plot the data. Identify the frequency bandgaps in the plot as the frequency ranges with at least 10 dB transmission drop compared to the reference transmission. Subsequently, export the raw data as mat or csv and use graphical tools (e.g., MATLAB, Origin Pro, MS Excel, etc.) to generate plots for further analysis.
6. Pitch-catch transmission tests with non-contact laser Doppler vibrometer (LDV)
NOTE: The experimental procedure involves setting up the test setup, acquiring the transmitted signal, and post-processing of measured data.
- Experimental preparation
- Choose a suitable excitation source based on numerical predictions for an operational frequency range.
- If operating frequencies exceed 75 kHz, choose an ultrasonic transducer, clean its surface, and cover it uniformly with a thin layer of a couplant (different for longitudinal and shear wave transducers25) before placing it on a sample.
- For low-frequency excitation (<50 kHz), choose a piezoelectric disc of suitable diameter (3-50 kHz) or a vibrational shaker (0-10 kHz) as an excitation source. The piezoelectric discs must be glued to a tested sample to ensure proper coupling.
- Ensure that the test specimen is clean and positioned securely. Apply a reflective tape to the test specimen at the intended point of signal acquisition for better signal detection by the laser.
- Adjust the position and angle of the LDV laser to direct it toward the reflective tape by ensuring that the laser is directed strictly perpendicular to the reflective tape and the standoff distance is set to an optimal value as prescribed in the LDV manual. Make sure to isolate the base table, where the specimen is kept, from any object that could induce electric or acoustic noise.
- Create an electric circuit by joining a computer to a signal generator, followed by an amplifier, which is connected to a piezo. The LDV is connected to an acquisition system or oscilloscope. The data acquisition system is, in turn, connected to a computer. Once a proper connection is established, begin the test.
- Choose a suitable excitation source based on numerical predictions for an operational frequency range.
- Signal generation and acquisition
NOTE: The signal generation and acquisition procedures are exemplified by using the SBench6 software.- Create two separate projects for signal generation and acquisition by selecting the proper hardware from the Start Manager Dialog for a generator and a digitizer. Click Start to initiate the process in the Input Mode tab and choose a recording mode. Preselect the Standard Single mode, allowing adjustment of parameters like Memsize (number of samples per channel).
NOTE: A recommended starting value is 32 kS. Pre-trigger and post-trigger refer to the number of samples that should be recorded before and after the trigger mode, as required. - Set the desired sampling rate under the Clock tab. By default, the maximum sampling rate for the selected recording mode is applied.
- Configure the triggering mode under the Trigger tab. Choose an appropriate mode, such as software triggering for immediate acquisition after the license card is ready. All input channels are accessible in the Input Channel tab.
- To initiate a single-shot recording, click the right-moving green arrow button. Recording stops automatically upon reaching the specified Memsize. Alternatively, opt for endless loop recording. End the recording using the Stop button. Recordings are shown on an analog display.
NOTE: When the generator card is connected, the Input Mode tab in the generator window switches to Output Mode. - Use the Easy Generator option of the measurement software to generate simple excitation functions like sine waves or rectangular pulses.
- Alternatively, employ a Function Generator to generate arbitrary mathematical functions. To do that, navigate to the New tab, choose Signal Calculations, and choose the Function Generator option.
- Ensure that the sample rate matches the internal clocking rate. Define the length of the signal and start the signal, which will then be shown on the analog display. A mathematical function can be typed in the formula field or loaded as a .txt file.
- Perform a fast Fourier transform (FFT) on the signal by selecting Signal Calculations under Input Channels and choosing FFT. Choose an appropriate window function (e.g., rectangular, Hanning, Hamming, etc.) for FFT calculation. To verify the accuracy of the generated signal, compute its Fast Fourier Transform (FFT) and confirm if the peak aligns with the frequency assigned to the signal.
- Inspect the configuration to ensure proper operation before starting the test by pointing the LDV laser at the vibration source (e.g., ultrasonic transducer, shaker, etc.), sending a signal, and calculating FFT. In another window of the measurement software, assign a digitizer license card and observe the received signal. Match FFT results in both windows before proceeding with the experiment.
- Start the experiment by pointing the LDV laser at the desired point of acquisition on the metamaterial sample. Generate a signal, record the data, and save it.
- Create two separate projects for signal generation and acquisition by selecting the proper hardware from the Start Manager Dialog for a generator and a digitizer. Click Start to initiate the process in the Input Mode tab and choose a recording mode. Preselect the Standard Single mode, allowing adjustment of parameters like Memsize (number of samples per channel).
- Data analysis and processing
- Analyze the frequency response data in the digitizer window to identify frequency bandgaps for validating numerical results.
- Export data as binary ASCII or MATLAB mat files for plotting using tools like OriginPro, MATLAB, etc.
Representative Results
The described protocol is illustrated by manufacturing and characterizing bone-shaped and metamaterial samples made of acrylonitrile butadiene styrene (ABS). The geometries of the samples are as follows. The dimensions of the dog bone-shaped samples for the tensile tests follow the designation D638−14. The metamaterial structure represents a continuous analog of a one-dimensional mass-spring model (Supplementary File 1) that is composed of 10 disks of radius 7 mm and 2 mm thickness located periodically at 20 mm, which are joined by thin beams of square cross-section 2 mm x 2 mm. STL file for dog-bone structure used for tensile testing can be found in Supplementary File 2.
3D printing of polymer samples
The steps of section 1 are followed to manufacture the metamaterial and bone-shaped samples using an FDM two-nozzle 3D printer. In the slicer software, Acrylonitrile Butadiene Styrene (ABS) filament is assigned for nozzle 1, while nozzle 2 is switched off since the samples are produced from a single material without support. The following print settings are used: infill density of 100%, linear infill pattern of 0.2 mm layer height, nozzle temperature of 245 °C, bed temperature of 100 °C, print speed of 40 mm/s, and fan speed of 3%. The sliced geometries are shown in Figure 1A. To keep the parts fixed during the print process, a thin layer of glue on the print bed surface is applied. Once the printing is finished (Figure 1B), the 3D printed structures are removed after the print bed is cooled down to room temperature. The final 3D-printed samples are shown in Figure 1C.
TGA and DSC
The TGA of the ABS polymer indicates a single-stage decomposition process, see Figure 2A. The measured onset temperature of decomposition is 390 °C, with complete decomposition occurring at around 420 °C. One observes 5% weight loss of the test sample corresponding to 363.6 °C, which served as the upper-temperature limit for the DSC test. DTG results reveal a peak decomposition rate at 404.5 °C. Figure 2B shows the results of the DSC test performed over a temperature range of 40 °C to 270 °C, indicating a glass transition temperature (Tg) of 100.4 °C and a melting temperature (Tm) of 216.5 °C.
DMA
The glass-transition temperature (Tg) from DSC serves as the upper temperature limit for the DMA test following the objective of this work to characterize ABS at room temperature. The DMA was performed using the DMA 8000, see Figure 3, on three samples, each of linear infill-pattern aligned at 0° (type 1) and 45° (type 2) to the reference  of the 3D printer. A frequency sweep from 0.1 to 100 Hz is employed with temperatures varying between 5 °C and 60 °C. The heating rate was adjusted to 2 °C/min, and the temperature was increased in increments of 5 °C with a 5 min isothermal pause at each step. The curves obtained at 12 different temperatures were shifted to a reference temperature of 25 °C using the Williams-Landel-Ferry (WLF) equation. The conclusive time-temperature superposition outcomes for type 1 and type 2 samples (Figure 4) reveal a flat line for storage modulus and loss modulus in the frequency range of 10-7 to 108 Hz. Some deviations are observed in the loss modulus and tan (δ) at certain points in the TTS curve.
of the 3D printer. A frequency sweep from 0.1 to 100 Hz is employed with temperatures varying between 5 °C and 60 °C. The heating rate was adjusted to 2 °C/min, and the temperature was increased in increments of 5 °C with a 5 min isothermal pause at each step. The curves obtained at 12 different temperatures were shifted to a reference temperature of 25 °C using the Williams-Landel-Ferry (WLF) equation. The conclusive time-temperature superposition outcomes for type 1 and type 2 samples (Figure 4) reveal a flat line for storage modulus and loss modulus in the frequency range of 10-7 to 108 Hz. Some deviations are observed in the loss modulus and tan (δ) at certain points in the TTS curve.
Tensile testing
Tensile tests were conducted utilizing an ultimate tensile machine (UTM), see Figure 5, with a maximum load capacity of 1 kN. The testing parameters included a maximum force of 980 N and a ramp time of 60 s. A recovery time of 10 s was set, and the tensile test machine recorded 10 data points for force per second. The high-resolution cameras of a DIC system captured 30 images per frame, and the analysis was done focusing on the shaded region identified as polygon 1 in Figure 6A. The average principal strain values within the shaded region are 1.317 (tensile strain) and -0.454 (compressive strain). Figure 6B shows the results for the Poisson's ratio, with an observed average value of 0.37. Figure 6C shows the results for Young's modulus, calculated from the slope of the unloading curve showing elastic regain, which yields a value of 0.543 GPa.
Finite element analysis
Figure 7A presents the geometry of a metamaterial considered for the transmission analysis, where the "Output plane" indicates the probe to measure transmitted signals. The numerically estimated transmission curve is shown in Figure 7B, for an out-of-plane excitation displacement of 1 μm along  of the incident plane shown for the model in Figure 7A. The drops in transmission level exceeding 20 dB, shown by a shaded region, represent frequency bandgaps at various frequency ranges.
of the incident plane shown for the model in Figure 7A. The drops in transmission level exceeding 20 dB, shown by a shaded region, represent frequency bandgaps at various frequency ranges.
Pitch-catch transmission tests
Figure 8 shows the setup used for the pitch-catch transmission test performed on a simple 1D continuous analog of a periodic mass-spring model made of commonly used ABS polymer (Figure 9A), using non-contact LDV. Figure 9B shows the results of the pitch-catch transmission test in the frequency domain for the 3D-printed ABS sample identical to the one shown in Figure 7A. The ceramic-based Ag-screened piezoelectric disc of radial resonant frequency 200 kHz (diameter 10 mm and thickness 0.2 mm) was used to apply a frequency sweep signal swept from 4 kHz to 40 kHz. The transmitted signal was acquired at the 10th unit cell from the excitation side. The recorded time-domain data were transformed to the frequency domain by applying the Fast Fourier Transform. The processed data reveal a signal drop of more than 20 dB at various frequencies, indicating the frequency bandgaps that are highlighted in blue in Figure 9B.

Figure 1: 3D printing of polymer samples. (A) Sliced geometry in the slicer software. (B) Ongoing 3D printing process. (C) 3D printed ABS sample for tensile testing as per ASTM standard D638. Please click here to view a larger version of this figure.
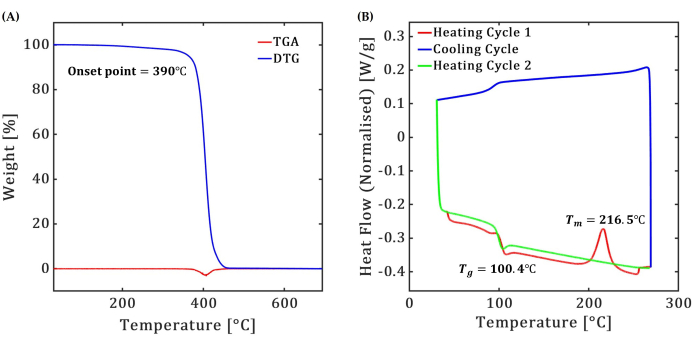
Figure 2: Thermogravimetric analysis (TGA) and differential scanning calorimetry (DSC). Thermal characterization results for the ABS polymer in (A) TGA and DTG and (B) DSC tests. Please click here to view a larger version of this figure.

Figure 3: Dynamic mechanical analysis. (A) DMA instrument and important parts. (B) Image of the single-cantilever test configuration (without sample). (C) Image of a clamped sample in the single-cantilever test configuration. Please click here to view a larger version of this figure.
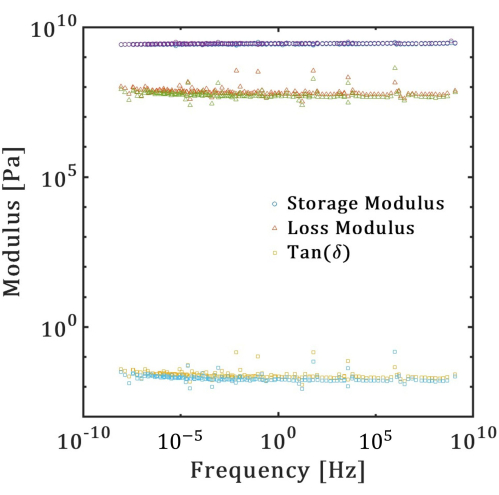
Figure 4: Time-temperature superposition outcomes. TTS results for ABS polymers 3D printed with a linear infill pattern aligned at 0° (type 1) and 45° (type 2) to the reference 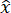 of the 3D printer: storage modulus, loss modulus, and tan(δ). Please click here to view a larger version of this figure.
of the 3D printer: storage modulus, loss modulus, and tan(δ). Please click here to view a larger version of this figure.
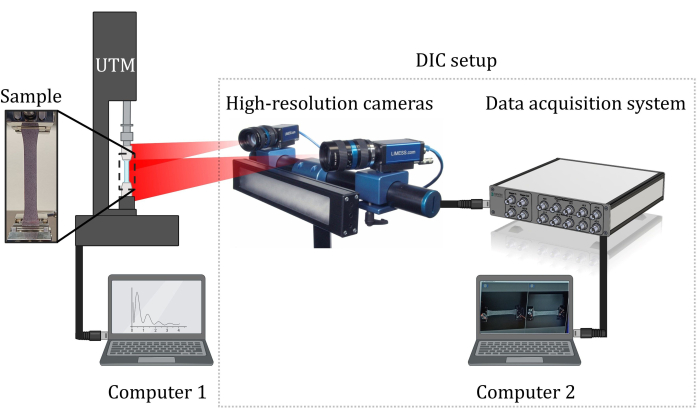
Figure 5: Tensile testing setup. Diagram of the tensile testing setup, including the universal tensile machine (UTM) coupled with a DIC setup. A magnified view of the sample is also shown to highlight the speckle pattern on the sample. Please click here to view a larger version of this figure.
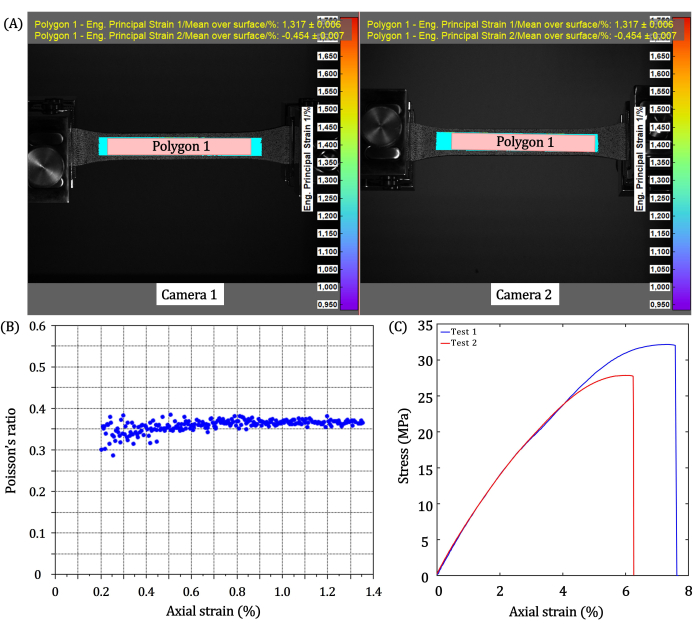
Figure 6: Results of tensile testing. (A) Image of the test sample acquired by both cameras of the DIC setup. Polygon 1 is the area considered for calculations; the sample was pulled from left to right. (B) Results for Poisson's ratio. (C) Stress-strain behavior of the 3D printed ABS bone-shaped samples (type 2) tested at 50 mm/min (Test 1) and 5 mm/min (Test 2). Testing was done on four samples. Please click here to view a larger version of this figure.
Figure 7: Finite element analysis. (A) A geometric model for numerical calculations of transmission; ax is the unit cell dimension, d is the diameter of the disc, and PML stands for perfectly matched layer. (B) Numerical results for transmission calculations, shaded regions represent frequency bandgap. Please click here to view a larger version of this figure.
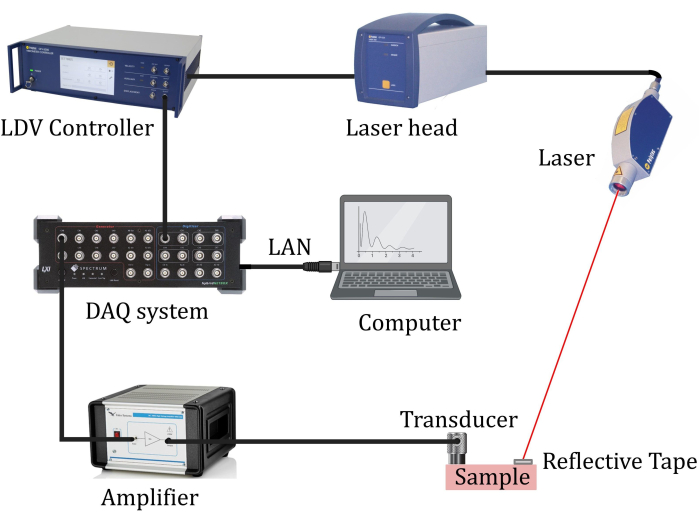
Figure 8: Pitch-catch transmission experiment setup. Testing setup for pitch-catch transmission experiments with a non-contact laser Doppler vibrometer used to measure mechanical vibrations transmitted through a sample. Please click here to view a larger version of this figure.
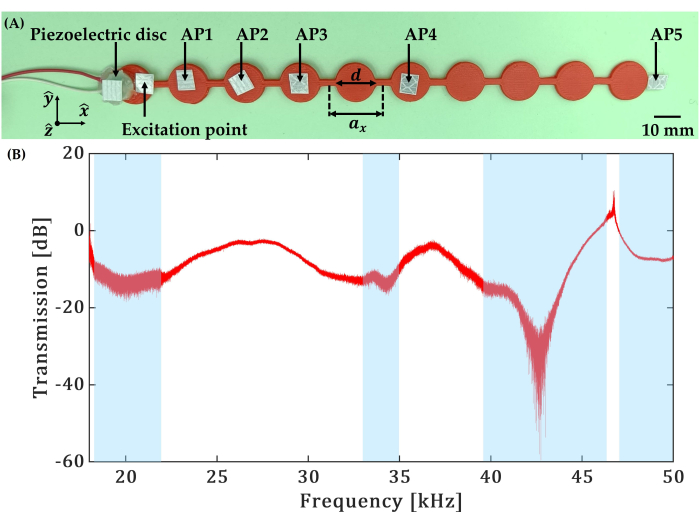
Figure 9: Results of pitch-catch transmission experiment. (A) A photo of the metamaterial structure of unit cell size ax = 20 mm with disk diameter d = 14 mm tested in the pitch-catch transmission experiment. A piezoelectric disc of radial resonant frequency 200 kHz is used to excite structural vibrations and reflective tape is pasted for acquisition at different points (AP1, AP2, AP3, AP4, and AP5) of the structure. (B) Experimental results from pitch-catch transmission test. Recordings for the incident and the transmitted signal were done at the excitation point and the acquisition point 5 (AP5), respectively. Shaded regions represent frequency bandgap estimated experimentally. Please click here to view a larger version of this figure.
| Test configuration | Test samples |
| Single Cantilever | Most samples, except thin films under 0.1 mm |
| Dual Cantilever | Comparatively soft materials if the single cantilever data are noisy |
| Three-point bending | Very stiff and large samples |
| Tension | Very thin films of thickness <0.2 mm |
Table 1: Test configurations suitable for different test samples for DMA, classified based on the sample stiffness.
| Test configurations | Length (mm) | Width (mm) | Thickness (mm) |
| Single Cantilever | 05–25 | 04–12 | 0.10–4.00 |
| Dual Cantilever | 25–45 | 04–12 | 0.10–4.00 |
| Three Point Bending | 25–45 | 04–12 | 0.50–4.00 |
| Tension | 10–25 | 04–10 | 0.01–0.20 |
Table 2: Dimensions of test samples for different test configurations in the DMA technique.
Supplementary File 1: STL file for 1D periodic structure. Please click here to download this File.
Supplementary File 2: STL file for dog-bone structure used for tensile testing. Please click here to download this File.
Discussion
The 3D printing procedure described in section 1 applies to most table-size FDM 3D printers. Yet, 3D printing from ABS can be tricky because this polymer is sensitive to temperature changes. Uneven heating or cooling can cause shrinkage of already printed parts, leading to warping, cracking, or delamination. To prevent these issues, it is suggested first to identify proper print settings based on a datasheet from the supplier. Next, it is advised to avoid strong temperature variations near the printed part during the printing process. It can be achieved by enclosing the 3D printer with a box or a chamber to maintain a stable warm environment.
Thermogravimetric analysis (TGA) is aimed here to identify the temperature at which the material decomposition initiates, as this temperature governs the maximum safe temperature for differential scanning calorimetry (DSC). TGA operates on the principle of measuring the mass loss of a material as a function of temperature. The DSC, in turn, measures key thermal parameters of a material, including the glass-transition temperature, melting point, and recrystallization temperatures. It operates based on the principle of detecting energy changes associated with phase transitions. Thus, TGA and DSC tests serve as complementary techniques to DMA.
It is crucial to analyze Tm from the DSC plot carefully, as subjecting the dynamic mechanical analyzer to a melted sample can damage the thermocouple of the instrument. Before loading the sample, one needs to ensure that the pan remains uncontaminated. Contamination of the sample with foreign substances can affect the thermal properties and introduce artifacts in the TGA and DSC curves. Careful identification of Tg and Tm is crucial as they serve as important parameters for DMA.
DMA measures the variation of material properties of the test sample with temperature, within the user-specified frequency range. The DMA instrument can do such measurements within the frequency range of 0.01-600 Hz. Variation of material properties of rheological simple polymers at frequency values outside this range can be predicted using the time-temperature superposition7. In this way, one obtains the viscoelastic properties of materials - loss modulus and complex viscosity. However, operating at temperatures near Tm can damage the dynamic mechanical analyzer and must be avoided. Besides, operating at temperatures near Tg, may result in inconsistent and unreliable results. Also, note that proper sample alignment is essential, ensuring that the sample is straight and has smooth, parallel edges without surface defects. The thermocouple must not touch the clamps at any point of the measurement to avoid damage.
The almost flat trends for the storage and loss moduli curves in Figure 4 reveal that the FDM-printed ABS primarily exhibits elastic behavior at room temperature. The flatness of the curve for the tangent of phase angle(δ), which is the ratio of storage modulus to loss modulus, indicates that the Tg of the material does not lie within the measured temperature range. Besides, the data for the two test samples with different orientations of the print pattern are indistinguishable, suggesting no significant effect of the print pattern on the moduli. It can be attributed to exceptionally low viscous losses in ABS and 100% infill density, which mask any effect of patterning. Note, however, that these results are more an exemption rather than a rule for 3D printed polymers as the viscous losses in other filaments are non-negligible. These losses emphasize the importance of conducting the DMA for 3D-printed polymers.
Tensile testing is a widely adopted technique for the mechanical characterization of materials. It provides quasi-static mechanical moduli, e.g., Young's modulus and Poisson's ratio, for a material of the test sample, often of a bone-like shape (Figure 1B). The digital image correlation (DIC) technique can be added to ensure the proper positioning of a test sample and to capture images of its deformed surface at each loading step, as well as to process the images to analyze strain and displacement fields. Although the integration of DIC yields a higher level of accuracy in results, it can lead to several challenges if not handled properly. It is important to apply a good speckle pattern, with a 3D residuum less than 0.4/pixel, while sample preparation for DIC. Ensure that the sample is well-focused and use proper calibration plates that fit best the field of view of the camera. The Young's modulus determined from tensile testing in this study, 0.543 GPa, agrees well with the value reported (0.751 GPa) by Samykano et al.26. UTM used for testing may have limitations in terms of accuracy, resolution, or capacity, which can affect the quality and reliability of the results. Incorrect sample preparation, including improper mounting or machining, can cause errors in the measurement. Slippage of the sample can be avoided by using abrasive papers for better contact between the sample and the jaws of the UTM. Additionally, many materials have anisotropic mechanical properties. Lack of attention to anisotropic behavior can lead to inaccurate predictions.
Numerical simulations to estimate bandgaps are essential to properly define the work frequencies for pitch-catch transmission tests4,8,27. The calculated data shown in Figure 7B are expectable for the analyzed metamaterial configuration shown in Figure 7A. Specifically, the transmission curve outside the bandgap frequency oscillates around a constant value with the oscillation peaks corresponding to natural frequencies of the finite-size periodic medium27. Within the bandgap, the transmission is strongly reduced validating the capability of this metamaterial to attenuate acoustic waves.
The reported simulation procedure (section 5) is general and not restricted to the analyzed geometry or specific viscoelastic behavior. Other metamaterial structures made of various viscoelastic materials can be successfully tested in the transmission analysis7,8,20,22,24. The material behavior is limited to linear elastic of viscoelastic as nonlinear materials cannot be analyz in the frequency domain4. Note that the transmission analysis in other finite-element packages may require other implementation steps and different terminology or commands for similar actions. Also, periodic boundary conditions and PML may be absent which requires searching for alternatives to reduce spurious wave reflections from the domain boundaries.
The pitch-catch transmission tests aim to estimate the portion of the acoustic wave energy transmitted through a (meta)material sample and identify (validate) bandgap frequencies. It is convenient to set up such a test based on preliminary numerical transmission data, which allows for identifying an operating frequency range that, in turn, enables the selection of a proper excitation source8,20,22,24. Typical equipment for transmission tests includes a signal generator to generate an excitation signal, an amplifier to increase the intensity of the signal, piezo elements (e.g., a piezoelectric disc or piezoceramic transducer) to transform electric signals into mechanical motions and vice versa, and a data acquisition system for recording transmitted signals7. One piezo element is tightly connected to a tested sample to excite a signal, while the other(s) is (are) used to receive a transmitted signal. The second piezo element is replaced here by a laser Doppler vibrometer (LDV) for non-contact measurements that deliver a better quality of recorded signals due to the extremely high sensitivity of the laser.
The averaged measured transmitted signal is in good agreement with the numerical predictions (Figure 7B and Figure 9B), as can be expected for a sample with extremely low viscous losses. The shown frequency-domain data are superimposed by noise owing to the high sensitivity of the laser. The advantages and flexibility of using LDV for data acquisition are clear. In addition to non-contact measurements and accurate data, the LDV enables measuring the signal at the excitation side by focusing the laser on the sample in the vicinity of a piezoelectric disk. This offers a possibility to evaluate the ratio of transmitted to the input signals as in numerical simulation which is especially useful for complex-structured metamaterials that exhibit an elevated level of internal wave reflections.
It can be concluded that the proposed protocol for characterizing viscoelastic metamaterials can be helpful for researchers working in this rapidly developing field to acquire data for a broad range of additively manufactured materials and to use these data in the analysis of metamaterials dynamics. Since exceptional damping properties offered by polymers due to viscoelastic effects make them a preferred choice over metallic or ceramic metamaterials, a deeper understanding of these effects is essential to further increase the applications of metamaterials in acoustic waveguiding, cloaking, underwater acoustics, sound absorption, medical imaging, energy harvesting, and many others.
Disclosures
All authors declare that they have no conflicts of interest.
Acknowledgements
S.B. and A.O.K. acknowledge the financial support for the OCENW.M.21.186 project provided by the Dutch Research Council (NWO).
Materials
| Name | Company | Catalog Number | Comments |
| Acrylonitrile Butadiene Styrene (ABS) | BASF | https://www.xometry.com/resources/3d-printing/abs-3d-printing-filament/ | Print temperature: 225-245 °C |
| COMSOL Multiphysics 6.0 | COMSOL | https://www.comsol.com/product-download/6.0 | Finite element software |
| DAQ system for DIC | Dantec Dynamics | https://www.dantecdynamics.com/components/daq-controllers/ | |
| Discovery DSC 25 | TA Instruments | https://www.tainstruments.com/dsc-25/ | Software: Trios; Pan: Aluminium |
| DMA 8000 | Perkin Elmer | https://www.perkinelmer.com/product/dma-8000-analyzer-qtz-window-ssti-clamp-n5330101 | Software: PerkinElmer |
| DN2.813-04 Spectrum hybridNetbox | Spectrum Instrumentation | https://spectrum-instrumentation.com/products/details/DN2813-04.php | 4-channel signal generator and digitizer; Software used: SBench6 |
| FDM 3D printer Ultimaker 3.0 | Ultimaker | https://ultimaker.com/3d-printers/s-series/ultimaker-s3/ | Slicer: Ultimaker Cura |
| Polytec laser unit OFV 534 | Polytec GmbH | https://www.polytec.com/eu/vibrometry/products | Laser and laser head, as a set |
| Polytec OFV-5000 vibrometer controller | Polytec GmbH | https://www.polytec.com/eu/vibrometry/products | LDV controller |
| Power amplifier Type 2718 | Bruel & Kjaer | https://www.bksv.com/en/instruments/vibration-testing-equipment/vibration-amplifiers/exciters/power-amplifier-type-2718 | Power output capability of 75 VA |
| PRYY-0110 | PI Ceramic | https://www.piceramic.com/en/products/piezoceramic-components/disks-rods-and-cylinders/piezoelectric-discs-1206710 | Ceramic-based, Ag-screened piezoelectric discs |
| Q400 DIC | Limess Messtechnik & Software GmbH | https://www.limess.com/en/products/q400-digital-image-correlation | Software: Istra4D |
| Thermogravimetric Discovery TGA 550 | TA Instruments | https://www.tainstruments.com/tga-550/ | Software: Trios; Pan: Aluminium |
| UniVert 1kN Tensile testing machine | Cell Scale biomaterials testing | https://www.cellscale.com/products/univert/ | Software: UniVert; load cell capacity: 1 kN |
| WMA-300 High speed high voltage amplifier | Falco Systems | https://www.falco-systems.com/High_voltage_amplifier_WMA-300.html | 50x amplification up to +150 V and -150 V with respect to ground |
References
- Lodge, T. P., Hiemenz, P. C. . Polymer Chemistry. Third edition. , (2020).
- Lakes, R. S. . Viscoelastic Solids. (1998), (2017).
- Manconi, E., Mace, B. R. Estimation of the loss factor of viscoelastic laminated panels from finite element analysis. J Sound Vib. 329 (19), 3928-3939 (2010).
- Moiseyenko, R. P., Laude, V. Material loss influence on the complex band structure and group velocity in phononic crystals. Phys Rev B. 83 (6), 064301 (2011).
- Frazier, M. J., Hussein, M. I. Viscous-to-viscoelastic transition in phononic crystal and metamaterial band structures. J Acoust Soc Am. 138 (5), 3169-3180 (2015).
- Krushynska, A. O., Kouznetsova, V. G., Geers, M. G. D. Visco-elastic effects on wave dispersion in three-phase acoustic metamaterials. J Mech Phys Solids. 96, 29-47 (2016).
- Krushynska, A. O., et al. Dissipative dynamics of polymer phononic materials. Adv Funct Mater. 31 (30), 2103424 (2021).
- Merheb, B., et al. Elastic and viscoelastic effects in rubber/air acoustic band gap structures: A theoretical and experimental study. J Appl Phys. 104 (6), 064913 (2008).
- Krushynska, A. O., et al. Emerging topics in nanophononics and elastic, acoustic, and mechanical metamaterials: an overview. Nanophotonics. 12 (4), 659-686 (2023).
- Renaud, F., Dion, J. -. L., Chevallier, G., Tawfiq, I., Lemaire, R. A new identification method of viscoelastic behavior: Application to the generalized Maxwell model. Mech Syst Signal Process. 25 (3), 991-1010 (2011).
- Lewandowski, R., Chorążyczewski, B. Identification of the parameters of the Kelvin-Voigt and the Maxwell fractional models, used to modeling of viscoelastic dampers. Comput Struct. 88 (1-2), 1-17 (2010).
- Lewińska, M. A., Kouznetsova, V. G., van Dommelen, J. A. W., Krushynska, A. O., Geers, M. G. D. The attenuation performance of locally resonant acoustic metamaterials based on generalised viscoelastic modelling. Int J Solids Struct. 126-127, 163-174 (2017).
- Lee, D., Kim, M., Rho, J. A finite element method towards acoustic phononic crystals by weak formulation. J Phys Condens Matter. 31 (37), 375901 (2019).
- Langer, P., Maeder, M., Guist, C., Krause, M., Marburg, S. More than six elements per wavelength: The practical use of structural finite element models and their accuracy in comparison with experimental results. J Comput Acoust. 25 (04), 1750025 (2017).
- Poggetto, V. F. D., Serpa, A. L. Elastic wave band gaps in a three-dimensional periodic metamaterial using the plane wave expansion method. Int J Mech Sci. 184, 105841 (2020).
- de Oliveira, V. B. S., Schalcher, L. F. C., dos Santos, J. M. C., Miranda Jr, E. J. P. Wave attenuation in 1-D viscoelastic phononic crystal rods using different polymers. Mater Res. 26, (2023).
- Xiao, Y., Wen, J., Wen, X. Broadband locally resonant beams containing multiple periodic arrays of attached resonators. Phys Lett A. 376 (16), 1384-1390 (2012).
- Kulpe, J. A., Sabra, K. G., Leamy, M. J. Bloch-wave expansion technique for predicting wave reflection and transmission in two-dimensional phononic crystals. J Acoust Soc Am. 135 (4), 1808-1819 (2014).
- Guo, Z., Sheng, M., Pan, J. Flexural wave attenuation in a sandwich beam with viscoelastic periodic cores. J Sound Vib. 400, 227-247 (2017).
- Valiya Valappil, S., Krushynska, A. O., Aragón, A. M. Analytical characterization of the dynamic response of viscoelastic metamaterials. Comput Mater Sci. 229, 112385 (2023).
- Shi, L., et al. Spectral element method for band-structure calculations of 3D phononic crystals. J Phys D Appl Phys. 49 (45), 455102 (2016).
- Matlack, K. H., Bauhofer, A., Krödel, S., Palermo, A., Daraio, C. Composite 3D-printed metastructures for low-frequency and broadband vibration absorption. Proc Natl Acad Sci U S A. 113 (30), 8386-8390 (2016).
- Van Belle, L., Claeys, C., Deckers, E., Desmet, W. On the impact of damping on the dispersion curves of a locally resonant metamaterial: Modelling and experimental validation. J Sound Vib. 409, 1-23 (2017).
- D'Alessandro, L., Krushynska, A. O., Ardito, R., Pugno, N. M., Corigliano, A. A design strategy to match the band gap of periodic and aperiodic metamaterials. Sci Rep. 10 (1), 16403 (2020).
- Theobald, P., Zeqiri, B., Avison, J. Couplants and their influence on AE sensor sensitivity. J Acoust Emiss. 26, 91-97 (2008).
- Samykano, M., et al. Mechanical property of FDM printed ABS: influence of printing parameters. Int J Adv Manuf Technol. 102 (9-12), 2779-2796 (2019).
- Hussein, M. I., Leamy, M. J., Ruzzene, M. Dynamics of Phononic Materials and Structures: Historical Origins, Recent Progress, and Future Outlook. Appl Mech Rev. 66 (4), 040802 (2014).
Explore More Articles
This article has been published
Video Coming Soon
ABOUT JoVE
Copyright © 2025 MyJoVE Corporation. All rights reserved