מיפוי פני השטח של אקסופלנטות דמויי כדור הארץ באמצעות עקומות אור בנקודה אחת

Summary

הפרוטוקול מחלץ מידע מתעקומות אור של אקסופלנטות ובונים את מפות פני השטח שלהם. היא משתמשת בעקומות אור של כדור הארץ, המשמש כאקסופלנטה פרוקסי, כדי להדגים את הגישה.

Abstract

פתרון מרחבי של תכונות אקסופלנטה מתצפיות של נקודה אחת חיוני להערכת המגורים הפוטנציאליים של אקסופלנטות. המטרה הסופית של פרוטוקול זה היא לקבוע אם עולמות פלנטריים אלה נמל תכונות גיאולוגיות ו / או מערכות אקלים. אנו מציגים שיטה לחילוץ מידע מתעקומות אור מרובות אורך גל בנקודה אחת ואחזור מפות פני השטח. היא משתמשת בפירוק ערך יחיד (SVD) כדי להפריד מקורות התורמים לווריאציות עקומת האור ומקנים את קיומן של מערכות אקלים מעוננות חלקית. באמצעות ניתוח של סדרת הזמן שהתקבלה מ- SVD, ניתן להסיק ייחוסים פיזיים של רכיבים עיקריים (מחשבים) ללא הנחות של מאפיינים ספקטרליים כלשהם. בשילוב עם גיאומטריית הצפייה, ניתן לשחזר מפות משטח אם נמצא שאחד המחשבים מכיל מידע על פני השטח. Degeneracy מקורו התכווצות של גיאומטריית פיקסל ומידע ספקטרום קובע את האיכות של מפות משטח משוחזרות, אשר דורש המבוא של סדירות. לצורך הדגמת הפרוטוקול, עקומות אור באורך גל מרובה של כדור הארץ, המשמש אקסופלנטה פרוקסי, מנותחים. השוואה בין התוצאות לאמת הקרקע מוצגת כדי להראות את הביצועים והמגבלה של הפרוטוקול. עבודה זו מספקת אמת מידה להכלה עתידית של יישומי אקסופלנטה.

Introduction

זיהוי עולמות ראויים למגורים היא אחת המטרות הסופיות באסטרוביולוגיה¹. מאז הגילוי הראשון², יותר מ 4000 exoplanets אושרו^{עד כה 3} עם מספר אנלוגים כדור הארץ (למשל, TRAPPIST-1e)⁴. לכוכבי לכת אלה יש תכונות מסלוליות וכוכבי לכת הדומות לאלה של כדור הארץ, ולכן הם עשויים להיות ראויים למגורים. הערכת המגורים שלהם מתצפיות מוגבלות היא חיונית בהקשר זה. בהתבסס על הידע של החיים על פני כדור הארץ, מערכות גיאולוגיות ואקלים הן קריטיות למגורים, אשר ולכן יכול לשמש תרגמים ביולוגיים. באופן עקרוני, ניתן היה לצפות בתכונות של מערכות אלה ממרחק גם כאשר לא ניתן היה לפתור כוכב לכת באופן מרחבי טוב יותר כנקודה אחת. במקרה זה, זיהוי תכונות גיאולוגיות ומערכות אקלימיות מתקיות אור חד-נקודתיות חיוני בעת הערכת המגורים של אקסופלנטות. מיפוי פני השטח של האקסופלנטות האלה הופך לדחוף.

למרות ההתפתלויות בין גיאומטריית הצפייה לתכונות ספקטרליות, מידע על פני השטח של אקסופלנטה נכלל בעקומות האור החד-נקודתיות שנפתרו בזמן, אותן ניתן להשיג ממרחק, ונגזר ממנו תצפיות מספיקות. עם זאת, מיפוי פני השטח הדו-ממדי (2D) של כוכבי לכת דמויי כדור הארץ עשויים להיות ראויים למגורים, ומאתגר בשל השפעת העננים. שיטות לאחזור מפות דו-ממדיות פותחו ונבדקו באמצעות עקומות אור מדומה^{וספקטרום ידוע 5,6,7,8}, אך הן לא הוחלו על תצפיות אמיתיות. יתר על כן, בניתוחים של תצפיות אקסופלנטה עכשיו ובביטיד הקרוב, הנחות של ספקטרום אופייני עשוי להיות שנוי במחלוקת כאשר קומפוזיציות פני השטח פלנטריות אינן מוגבלות היטב.

בנייר זה, אנו מדגימים טכניקת מיפוי פני השטח עבור כוכבי לכת אקסו-פלנטות דמויי כדור הארץ. אנו משתמשים ב- SVD כדי להעריך ולהפריד מידע ממקורות שונים הכלולים בעקומות אור באורך גל מרובה ללא הנחות של ספקטרום ספציפי כלשהו. בשילוב עם גיאומטריית הצפייה, אנו מציגים את השחזור של מפות פני השטח באמצעות מידע משטח שנפתר בזמן אך מרחבי. לצורך הדגמת שיטה זו, תצפיות של שנתיים באורך גל יחיד של כדור הארץ שהושגו על ידי מצפה האקלים בחלל העמוק/ מצלמת הדמיה פוליכרומטית של כדור הארץ (DSCOVR/EPIC; www.nesdis.noaa.gov/DSCOVR/spacecraft.html) מנותחות. אנו משתמשים בכדור הארץ כאקסופלנטה פרוקסי כדי להעריך שיטה זו כי כרגע תצפיות זמינות של אקסופלנטות אינן מספיקות. אנחנו מצרףים את הקוד עם הנייר כדוגמה. הוא פותח תחת פיתון 3.7 עם אנקונדה וחבילות מרפא, אבל המתמטיקה של הפרוטוקול יכול להיעשות גם בסביבות תכנות אחרות (למשל, IDL או MATLAB).

Protocol

1. כיוונון תכנות

1. הגדר את סביבת התיכנות עבור הקוד המצורף. נדרש מחשב עם מערכת ההפעלה Linux, מכיוון שחבילת המרפא אינה זמינה ב- Windows. הקוד אינו יקר מבחינה חישובית, כך שמחשב אישי רגיל יכול לטפל בפרוטוקול.
2. בצע את ההוראה (https://docs.anaconda.com/anaconda/install/linux/) כדי להתקין את אנקונדה עם Python 3.7 במערכת ולאחר מכן השתמש בפקודות הבאות במסוף כדי להגדיר את סביבת התיכנות:
   $ קונדה ליצור --שם פיתון myenv = 3.7
   $ קונדה להפעיל myenv
   $ קונדה להתקין אנקונדה
   $ קונדה להתקין מרפא
   הערה: שלבים אלה עשויים להימשך עשרות דקות בהתאם לחומרה ולמהירות האינטרנט. ניתן לשנות את שם הסביבה 'myenv' בשתי שורות הפקודה הראשונות לכל מחרוזת אחרת.

2. קבלת עקומות אור באורך גל רב והצגת גיאומטריה מתצפיות

1. בגיאומטריית הצפייה, כלול את קו האורך והרוחב של תת-כוכבי ואת נקודות תת-הצופה עבור כל מסגרת זמן מתאימה.
   כדי להשתמש בקוד המצורף הבא, ודא של שני קבצים אלה יש תבנית זהה לזה של LightCurve.csv ו- Geometry.csv.
2. הפעל PlotTimeSeries.py כדי לדמיין את הנתונים ולבדוק את האיכויות שלהם. שתי דמויות LightCurve.png וגיאומטריה.png ייווצאו(איור משלים 1-2). ייתכן שיהיה צורך להתאים פרמטרים בקודים אלה ובעקבות התווייתם אם מוחלים על תצפיות שונות.
   $ פיתון PlotTimeSeries.py LightCurve
   $ פיתון PlotTimeSeries.py גיאומטריה

3. לחלץ מידע פני השטח עקומות אור

1. מרכז זמן נפתר ים רב גל אלבדו עקומות אור של exoplanet ולנרמל אותם על ידי סטיית תקן המתאימה בכל אורך גל. התוצאה היא חשיבות שווה של כל ערוץ.
   
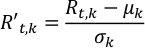
   כאשר_{R't' t, k} ו R_t,k הם אלבדו קנה מידה ונצפה בשלב t-th ואורך הגל k-th, בהתאמה; μ_k σ_k הם סטיית התקן והמרשיעה של סדרת הזמן albedo באורך הגל k-th.
   1. הפעל Normalize.py כדי לנרמל את עקומות האור, R_{t, k}. הפלט נשמר ב- NormalizedLightCurve.csv.
      פיתון Normalize.py
2. הפעל PlotTimeSeries.py כדי לדמיין את עקומות האור המנורמלות. איור מנורמלLightCurve.png ייווצר(איור משלים 3).
   $ פיתון PlotTimeSeries.py מנורמלאורקור
3. החל SVD על עקומות אור albedo בקנה מידה כדי למצוא מחשבים דומיננטיים ואת סדרת הזמן המתאימה שלהם.
   
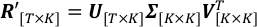
   בצד שמאל, T ו-K הם המספר הכולל של שלבי זמן ואורך גל תצפית; R' היא המטריצה של תצפיות אלבדו בקנה מידה, אשר (t, k)-אלמנט הוא R'_{t, k}. בצד ימין, עמודות של V הן מחשבים, וקטורים אורתונורמליים המגדירים את שטח פרוייקטי SVD ל; Ω היא מטריצה אלכסונית, אשר (k,k)-th אלמנט הוא סטיית התקן של עקומות אור קנה מידה לאורך ציר k-th המוגדר על-ידי העמודה k-th של V; עמודות U הן סידרת הזמן המתאימה של כל מחשב ב- V.
   1. תריץ SingularValueDecomposition.py כדי להרקקב את ר'. U , Ω ,V T המתוצריםנשמרים בקבצי הפלט U.csv, SingularValue.csv V_T.csv, בהתאמה.
      פיתון SingularValueDecomposition.py
4. השתמש PlotTimeSeries.py ו- PlotSVD.py כדי לדמיין באופן חזותי את תוצאת ה- SVD. שלוש דמויות U.png, סיגמא.png V_T.png ייווצאו(איור משלים 4-6).
   $ פיתון PlotTimeSeries.py U
   פיתון PlotSVD.py
5. נתח תרומות וסדרת זמן מתאימה של מחשבים כדי לקבוע את סדרת המחשבים המכילה מידע על פני השטח.
   1. השווה את הערכים הייחודיים באלכסון של Ω. אקסופלנטה מעונן חלקית דמוית כדור הארץ צפויה להיות בעלת שני ערכים ייחודיים דומיננטיים דומים.
      הערה: Ω עשוי להכיל פחות או יותר משני ערכים ייחודיים דומיננטיים, הנדונים להלן.
   2. השווה את תבניות סדרת הזמן של שני המחשבים הדומיננטיים. המחשב המכיל מידע על פני השטח נוטה להיות בעלי צורה רגילה יותר מהמחשב השני. בשל האקלים האורך והופע מחדש של פני השטח עם שינויים קטנים בשני ימים רצופים, סדרת הזמן המקבילה נוטה להיות וריאציה יומית קבועה בערך.
   3. חשב את התקופות של שני המחשבים הדומיננטיים באמצעות תקופה Lomb-Scargle^9,10 כדי לאשר את בחירת המחשב. המחשב המכיל מידע פני השטח נוטה להיות שיא גבוה יותר המתאים לתקופת סיבוב בספקטרום צפיפות צריכת החשמל.
   4. הפעל Periodogram.py כדי להשיג את ספקטרום צריכת החשמל של סידרת הזמן של כל מחשב. ספקטרום צריכת החשמל נשמרים ב- Periodogram.csv.
      פיתון Periodogram.py
   5. הפעל PlotPeriodogram.py כדי לדמיין תקופות תקופות אלה ואשר את בחירת המחשב. איור תקופה.png ייווצר(איור משלים 7). קוד התווייתו הנוכחי מוסיף בשורות מקווקווים המייצגים מחזורים שנתיים, חצי שנתיים, יומיים וחצי-יומיים לעיון, אשר ייתכן שיהיה צורך לשנות כאשר הם מוחלים על תצפיות אחרות.
      פיתון PlotPeriodogram.py
   6. בחר את המחשב, v_j, המכיל מידע פני השטח ואת סדרת הזמן שלה, u_j.
      
      
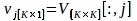
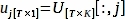
      כאשר V[:,j] ו- U[:,j] הם העמודות j-th של V ו- U,בהתאמה; j הוא האינדקס של מחשב להסיק בשלב 3.3 המכיל מידע פני השטח.

4. לבנות מפת פני שטח פלנטרית

1. השתמש בשיטת הפיקסליזציה של אזור שוויון הירארכי (HEALPix)¹¹ כדי לפיקסל את מפת האחזור. הוא מחלק משטח כדורי של כוכב לכת לפיקסלים עם אותו אזור והפצה אחידה. הוסף את הערך הלא ידוע של הפיקסל p-th כ- x_p.
   1. הפעל HEALPixRandom.py כדי להמחות את שיטת הפיקסליזציה. דמות HEALPixRandom.png ייווצר(דמות משלימה 8). ניתן לשנות_את הפרמטר N בצד בשורה 17 עבור רזולוציות שונות. שלב זה עשוי להימשך מספר שניות עד דקות, בהתאם לרזולוציה.
      פיתון HEALPixRandom.py
2. לחשב את המשקל של הפיקסל p-th בתצפיות בשלב t-th, w_t,p, באמצעות גיאומטריית צפייה.
   
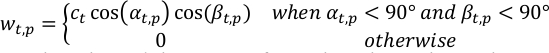
   כאשר α_t,p, β_{t,p הם} השמש וזוויות zenith החללית בפיקסל p-th בשלב t-th; c_t הוא מונח נורמליזציה של ההתבוננות t-th כך שסכום המשקל הכולל בכל שלב הוא אחדות.
   הערה: הגיאומטריה היא הניח להיות ידוע בשלב זה, או ניתן לגזור מניתוח אחר, אשר נדון להלן.
   1. הפעל ComputeWeight.py כדי לחשב את_{w t, p}. שנה את הערך של N_side בשורה 23 עבור רזולוציות אחרות של המפה המאוחזרת. הפלט נשמר כ- W.npz בשל גודלו.
      פיתון ComputeWeight.py
3. השתמש PlotWeight.py כדי לדמיין משקולות אלה. מספר דמויות, אחת בכל שלב, ייווצרתי בתיקיה משקל. מיזוגם תוצאה של וידאו משלים 1, המציג כיצד המשקל של כל פיקסל משתנה עם הזמן. שלב זה עשוי להימשך שעות עקב המספר הגדול של פריטים חזותיים.
   פיתון PlotWeight.py
4. שלב גיאומטריה ותצפיות כדי להגיע לבעיית רגרסיה ליניארית.
   
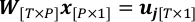
   כאשר P הוא המספר הכולל של אחזור פיקסלים; W היא מטריצת המשקל עם w_t,p כאלמנט (t, p)-th; x מורכב מ- x_p כרכיב p-th, שהוא הכמות שיש לפתור בבעיה זו.
   לפתור את בעיית הרגרסיה ליניארית עם התאמה סדירה של נורמה L-2.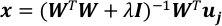
   
   כאשר אני מטריצת הזהות ו- ω הוא פרמטר ההתעוות.
   הערה: 10^-3 הוא ערך טוב עבור ω כאשר T ~ 10⁴ ו P ~ 3 * 10³. יש להתאים להם על-ידי השוואת הערכים של שני המונחים בשגיאה מרובעת רגילה, e, כפי המוצג להלן.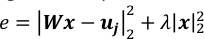
   
   1. הפעל LinearRegression.py כדי לפתור את בעיית הרגרסיה הליניארית. התוצאה של x נשמרת בקובץ PixelValue.csv. שנה את הערך של ω בקו 16 עבור חוזקות שונות של סדירות.
      פיתון LinearRegression.py
5. המר x למפת פני שטח דו-ממדית בהתאם לכלל המיפוי של HEALPix.
   1. הפעל PlotMap.py כדי לבנות את המפות המאוחזרות באמצעות פרמטרים שונים של התאמה רגילה. שלוש Map_-2.png, Map_-3.png ו-Map_-4.png ייווצרה עם ההגדרה הנוכחית(איור משלים 9). הקשר בין מדדי הפיקסלים למיקומם במפה מתואר במסמך HEALPix¹¹. שלב זה לוקח עשרות שניות.
      פיתון של PolotMap.py

5. הערכת אי-ודאות במפה המאוחזרת

1. לשכתב את בעיית הרגרסיה ליניארית בשלב 4.3 עם "הערך האמיתי" של x כמו z ורעש התצפית, ε.
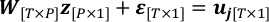
   1. נניח ε לעקוב אחר N הפצה Gaussian (0, σ²I_[T*T]) ולהעריך את התהודה שלה. T-P היא מידת החופש של u j_{מהתבוננות} כאשר המפה שאוחזרה קבוע.
      
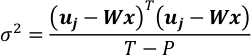
   2. שלב משוואות בשלבים 4.4 ו- 5.1. התוצאה היא וקטור גאוסיאני של x.
      
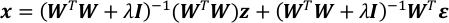
   3. מחשב את הציפייה ואת מטריצת התהודה של x.
      
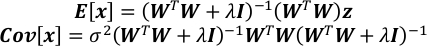
   4. השג את חוסר הוודאות של כל רכיב ב- x כבסיס הריבועי של הרכיב המתאים באלכסון של Cov[x].
      
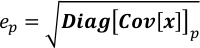
      כאשר e_p הוא חוסר הוודאות של x_p; דיאג[Cov[x]]_p הוא p-th אלמנט באלכסון של Cov[x].
   5. הפעל Covariance.py כדי לחשב את מטריצת התהודה של x. התוצאה נשמרת ב- Covariance.npz בשל גודלה. שלב זה לוקח עשרות שניות עד דקות בהתאם לגודל של W.
      פיתון Covariance.py
2. המר e_p למפת הדו-ממדית שאוחזרה בהתאם לכלל המיפוי של HEALPix.
   1. הפעל PlotCovariance.py כדי לדמיין את Cov[x] ולמפה את אי הוודאות e_p למפה המאוחזרת. שתי דמויות .png וחוסר ודאות.png ייווצרו(איור משלים 10-11).
      פיתון PlotCovariance.py

תוצאות

אנו משתמשים בעקומות אור מרובות אורך גל של נקודה אחת בכדור הארץ כדי להדגים את הפרוטוקול, ולהשוות את התוצאות לאמת הקרקע כדי להעריך את איכות מיפוי פני השטח. תצפית בשימוש כאן מתקבלת על ידי DSCOVR / EPIC, שהוא לוויין הממוקם ליד הנקודה Lagrangian הראשון (L1) בין כדור הארץ לשמש לוקח תמונות בעשרה אורכי גל של פנ?...

Discussion

אחת הדרישות הקריטיות של הפרוטוקול היא היתכנות של חילוץ מידע פני השטח מעקומות אור, התלויות בכיסוי הענן. בשלב 3.5.1, הערכים היחסיים של המחשבים עשויים להיות שונים בין אקסופלנטות. במקרה של כדור הארץ, שני המחשבים הראשונים שולטים בווריאציות עקומת האור, ומתאימים לעננים ומשטחים בלתי תלויים לפני השט...

Materials

Name	Company	Catalog Number	Comments
Python 3.7 with anaconda and healpy packages			Other programming environments (e.g., IDL or MATLAB) also work.