גלים עומדים
Overview
מקור: אריאנה בראון, אסנטה קוריי, PhD, המחלקה לפיזיקה ואסטרונומיה, בית הספר למדעי הפיזיקה, אוניברסיטת קליפורניה, אירווין, קליפורניה
גלים עומדים, או גלים נייחים, הם גלים שנראים לא מתפשטים ומיוצרים על ידי הפרעה של שני גלים הנעים בכיוונים מנוגדים עם אותו תדר ומשרעת. גלים אלה נראים לרטוט למעלה ולמטה ללא תנועה ליניארית והם מזוהים בקלות רבה ביותר בתקשורת סופית רוטט כמו מיתר גיטרה קטוף, מים באגם, או אוויר בחדר. לדוגמה, אם מחרוזת קבועה בשני קצות ושני גלים זהים נשלחים באורך, הגל הראשון יפגע במחסום הקצה וישקף בחזרה בכיוון ההפוך, ושני הגלים יעלו כדי לייצר גל עומד. תנועה זו היא תקופתית עם תדרים המוגדרים על ידי אורך המדיום והיא דוגמה חזותית לתנועה הרמונית פשוטה. תנועה הרמונית פשוטה היא תנועה שמתנדנדת או תקופתית, שבה הכוח המחזיר הוא פרופורציונלי לעקירה, כלומר ככל שמשהו נדחף רחוק יותר, כך הוא דוחף בחזרה חזק יותר.
מטרת הניסוי הזה היא להבין את התפקידים של סופרפוזיציית גל והשתקפות ביצירת גלים עומדים, ולנצל את המושגים האלה כדי לחשב את התדרים המהדהדים הראשונים, או הרמוניה, של גלים עומדים על slinky. לכל תדר שעצם מייצר יש דפוסי גל עומדים משלו, שבהם הגל עם התדירות הנמוכה ביותר האפשרית נקרא התדירות הבסיסית. הרמוניה היא גל שיש לו תדירות פרופורציונלית לתדר הבסיסי על ידי מספרים שלמים שלמים.
Principles
כאשר שני גלים מגיעים לאותה נקודה בנתיב בו זמנית, הם מתערבים. המשרעת של הגל המתקבל היא סכום המשרעת של שני הגלים הליניאריים (תוצאה ישירה של עקרון הסופרפוזיציה לגלים ליניאריים). שני הגלים האלה עוברים זה בזה מבלי לשנות זה את נתיביו או מהירויותיו של זה. הפרעה בונה מתרחשת כאשר המשרעת של הגלים להוסיף, כפי שהם מגיעים בשלב. כאשר הגלים נפגשים מחוץ לפאזה, המשרעת שלהם מחסרת והם עוברים הפרעות הרסניות. אם שני גלים עם אותה משרעת עוברים הפרעות הרסניות, המשרעת שלהם מתבטלת(איור 1).

איור 1: שני גלים עם משרעת שווה. משמאל: הפרעה בונה. מימין: הפרעה הרסנית.
כאשר גל נודד פוגש גבול (כלומר,מדיום אחר), חלק מהאנרגיה שלו משתקפת, חלקם מועברים למדיום החדש, וחלקם נספגים. עבור תרחיש גל משתקף מושלם, שבו כל האנרגיה משתקפת ולכן אין צורך להאכיל אנרגיה חיצונית למערכת, האנרגיה נשמרת. עבור גל הנע על מדיום עם גבולות קבועים, כמו מחרוזת סופית, זה ישקף את הגבול הסופי ולחוות שינוי פאזה של 180 מעלות צלזיוס. אם תהליך זה יימשך פרק זמן ממושך, הגלים המקפצים הלוך ושוב בין הגבולות יפריעו וייצרו תבנית נייחת המכונה גל עומד (איור 2). הנקודות של משרעת מינימלית (צמתים) הן נקודות שבהן הגלים יש שלבים הפוכים ולבטל אחד את השני. הנקודות של משרעת מקסימלית (antinodes) הן נקודות שבהן הגלים יש את אותו שלב ואת המשרעת שלהם בהתאמה לשלב.
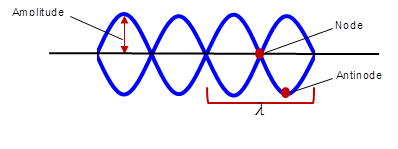
איור 2: גל עומד על מדיום באורך 2λ. זהו גם ייצוג חזותי של ההרמוניה הרביעית.
הגל הפשוט ביותר, המכונה לעתים התדירות הבסיסית, מתרחש כאשר אורך המחרוזת L הוא 1/2λ, שבו λ הוא אורך הגל. זה אומר,
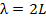
כך שהרטט הראשון במחרוזת עם נקודות קבועות נראה דומה לפרופיל של חבל קפיצה בתנועה. כדי להפוך את הגל העומד האפשרי הבא, צומת נוסף במרכז, ו- L הופך שווה ערך ל- λ: התוצאה היא תבנית גל עומדת עם אורך גל קצר יותר. דפוסי גלים עומדים עם אורכי גל קצרים יותר מהתדר הבסיסי ידועים כהרמוניקה. בהמשך להוספת צמתים, אנו מוצאים כי:
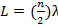 (משוואה 1)
(משוואה 1)
כאשר n הוא מספר הצמתים וההרמוני המתקבלת מכונה לעתים nההרמוני. (הערה: חלק מתייחסים לתדר הבסיסי כהרמוני הראשון, בעוד שאחרים מתייחסים n = 2 הרמוני כמו ההרמוני הראשון).
בגל מתפשט, האנרגיה מועברת יחד עם הגל. כאשר מקטע אחד נע כלפי מעלה, הוא מפעיל כוח על החלק הבא, ומזיז אותו דרך תזוזה. במילים אחרות, העבודה נעשית. נקודות שאינן נתקלות בהעתקה, כמו צומת בגל עומד, אינן יכולות לעבוד על המקטע השכן. לפיכך, אין אנרגיה המועברת על פני צומת על חוט, ואנרגיה אינה מתפשטת בגל עומד. במקום זאת, האנרגיה של גל עומד מתחלפת בין אנרגיה פוטנציאלית אלסטית כאשר הגלים נייחים לרגע במשרעת המרבית שלהם, לבין אנרגיה קינטית כאשר החוט שטוח באמצע תנודה וחלקיק על נטינודה יש מהירות כיוונית מקסימלית. בנוסף, שקול חלקיק הממוקם על פיסת חוט העוברת תנועת גל עומדת. מכיוון שגלים עומדים גורמים לתנועה פשוטה הלוך ושוב, נראה כי חלקיק זה נע קדימה ואחורה בקצב תקופתי מדוד. בגלים עומדים, תנועה תנודה זו והקשר בין אנרגיה אלסטית ופוטנציאלית מתוארים כתנועה הרמונית פשוטה, ולכן יש את המאפיינים הנצפים של תדירות f ונקודה T. בתרחיש גל העמידה, התדירות מוגדרת כמספר מחזורי התנודה ליחידת זמן, והתקופה היא הזמן הנדרש כדי לבצע מחזור אחד שלם, או:
 (משוואה 2)
(משוואה 2)
במעבדה זו, נחקור את כל המאפיינים הללו על ידי יצירת גלים שונים וגלים עומדים באמצעות slinky.
Procedure
1. התבוננות בסופרפוזיציה ובהשתקפות של פולסים סלינקיים
- למתוח קפיץ slinky או פלדה לאורך על פני רצפה או מסדרון, עם תלמיד אחד מחזיק קצה אחד וסטודנט אחר מחזיק את השני. השתמש בקלטת כדי לסמן שני 'מחסומים' באורך של כ-30 ס"מ מאמצע החלקלק, בכל צד. חזור עם מחסומים שנמצאים במרחק של שני מטרים מהאמצע בכל צד.
- בתורו שיגור פולסים (jerking slinky מרחק קטן אופקית ומיד הצמדה בחזרה לנקודת ההתחלה) עם משרעת להישאר בתוך המחסומים המסומנים.
- לאחר מכן, נסו לשגר פולסים זהים עם אותה קוטביות בו זמנית משני הקצוות ושימו לב מה קורה כאשר הפולסים נפגשים. הגל המודבק אמור להכפיל את המשרעת, לחצות את המחסומים המודבקים הראשונים ולפגוע במחסומים המודבקים השניים.
- עכשיו, לשגר פולסים זהים אבל עם קוטביות הפוכה בו זמנית ולהתבונן superpositions הדופק. הפעימות צריכות לבטל זו את זו כשהן מתבטלות, ואז להמשיך לנסוע, לעולם לא לגעת במחסומים.
- תקן קצה אחד של slinky על ידי החזקתו בחוזקה בעמדה. שלח פעימה אחת למטה למיקום הקבוע והתבונן במשרעת הגל על השתקפות. זה ישקף בחזרה עם קוטביות הפוכה.
2. מדידת תדירות הגלים העומדים על מעיין
- למתוח את slinky על פני חדר או מסדרון ולמדוד ולתעד את האורך המתוח.
- כאשר קצה אחד קבוע מתנועה (מוחזק בחוזקה), התחל להחליק בעדינות את הקצה השני אופקית בתנועה עקבית עד למציאת גל העמידה של התדר הבסיסי. עבור הרמוניה זו, צריך להיות רק פסגת גל אחת עם משרעת אחת נע קדימה ואחורה, כמו הפרופיל של חבל קפיצה בתנועה. השתמש בשעון עצר כדי לתעד את הזמן שלוקח למספר מחזורי גלים. מחזור שלם אחד מתחיל כאשר נוצרת נטינודה בצד אחד, מחליקה דרך המרכז כדי ליצור נטינודה בצד השני ולאחר מכן חוזרת למיקומה המקורי. השתמש במדידות אלה כדי לחשב את התדירות, התקופה ואורך הגל עבור גל זה באמצעות משוואות 1 ו- 2.
- הגדל את מהירות הקצה הזזה עד ההרמוני הבא (n = 2) מושגת. עבור הרמוניה זו, צריך להיות שני פסגות גל בצדדים מנוגדים נעים בכיוונים מנוגדים, וזה עשוי להיראות כמו הקרנה דו-כיוונית של האות 'של' מסתובב. מדוד את התדירות, ולאחר מכן חשב את התקופה ואת אורך הגל עבור הגל הזה. מהו היחס בין תדר זה לתדר הבסיסי?
- חזור על השלב הקודם עבור ההרמוני הבא (n = 3).
Results
| הרמוני (n) | מחזורים | זמן כולל (ים) | תדר (הרץ) | f/f0 | תקופה (ים) | אורך גל (ז) |
| 1 | 10 | 19.2 | 0.521(נ' 0) | 1 | 1.210 | 16 מטר |
| 2 | 10 | 9.75 | 1.026 | 1.97 | 0.975 | 8 מטר |
| 3 | 10 | 6.21 | 1.601 | 3.07 | 0.625 | 5.33 מטר |
טבלה 1: סעיף 2 - אורך אביב מתוח = 8 m
בסעיף 1, עקרונות של סופרפוזיציה גל והשתקפות במדיום סופי מוצגים ומאושרים כמו פולסים נשלחו לאורך של slinky. באופן ספציפי, אנו רואים שכאשר שני גלים עם משרעת זהה ופאזה נפגשים, הם עוברים הפרעות קונסטרוקטיביות והמשרעת שלהם מוסיפה. באופן דומה, אנו רואים שכאשר שני גלים עם קוטביות הפוכה (שינוי פאזה של 180 מעלות צלזיוס) ומשכוכים זהים נפגשים, הם עוברים הפרעות הרסניות והמשרעת שלהם מתבטלת. האחרון של עקרונות אלה הוא המפתח בהבנת דפוסי גל עומד.
בסעיף 2, הצמתים והנטינודות של הערמומיות נראו בקלות בתדרים שונים. ככל שמספר הצמתים גדל, כך גם התדירות. אורך הגל הוא ביחס הפוך לתדירות, כך שבאופן טבעי יש ירידה אורך הגל. התדרים של ההרמוניות הם כפולות מספר שלם חיוביות של התדר הבסיסי המתאים ל- n. לדוגמה, באמצעות n = 2 הרמוני, התדירות נמדדת ומוגדרת כמספר המחזורים ליחידת זמן:
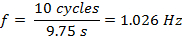
התקופה מוגדרת כהופכי של התדירות (משוואה 2) והיא שווה ל:
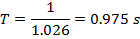
אורך הגל מוגדר במשוואה 1 כ:
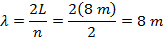
לבסוף, אנו יכולים לראות את הקשר ה-מספר שלם-פרופורציונלי בין ההרמוניות לבין התדירות הבסיסית על ידי חישוב:
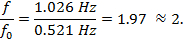
Application and Summary
בניסוי זה, המושגים של סופרפוזיציית גלים וגלים עומדים נחקרו בשתי הפגנות. השתקפות גלים והפרעה בונה מול הרסנית הוצגו בהדגמה הראשונה. בשנייה, השינויים בתדירות ובתקופה נמדדו ותדרים הרמוניים גבוהים יותר נמצאו כפולות שלמים של התדירות הבסיסית.
דוגמה מפורסמת לגלים עומדים בעולם האמיתי הם המיתרים על גיטרה, או כל כלי מיתר. במכשירים אלה, מחרוזת קטפה פולטת תדר מסוים בהתאם לתדירות מתוחה וצפופה של המחרוזת ולאורך המיתר. כל מחרוזת רק עושה הערות מסוימות כי רק גלים עומדים מסוימים, או הרמוניות, יכול להיווצר על מחרוזת זו. המוזיקאי יכול להשתמש באצבעותיהם כדי לקצר את אורך המיתר, יצירת צומת חדש וסדרת הרמוניות חדשה שהם פרופורציונליים לתדר הבסיסי. תנודות שאינן בתדר הנכון, נגיד אצבעות שמצמידות את המיתרים לדאגה שאינה מאפשרת גל עומד באורך המיתר הזה, יישמעו מוזרים ובסופו של דבר יבטלו את עצמן.
גלים עומדים מתרחשים גם בטבע, לעתים קרובות בגופי מים תחומים כמו אגמים ונמלים. לפעמים, הם יכולים להיווצר על קרקעית נהר המאפשרת לגולשים בנהר לרכוב על הגל הזה במשך תקופה ממושכת מבלי לזוז בפועל. בדרך כלל, הם נוצרים כאשר כמות גדולה של מים זורמת מעל חסימה, כמו סלע גדול, בקצב מהיר. כשהמים זורמים מעל הסלע ומתרסקים מאחוריו, הם יוצרים גל גדול בכיוון ההפוך של זרם הנהר שמפריע לגל המים. לפיכך, נוצר גל עומד וגולשי נהר יכולים לרכוב עליו כל עוד שיווי המשקל שלהם יאפשר להם מכיוון שהגל ככל הנראה לא יסתיים תוך שניות.
Skip to...
Videos from this collection:

Now Playing
גלים עומדים
Physics II
49.9K Views

שדות חשמליים
Physics II
77.6K Views

פוטנציאל חשמלי
Physics II
105.1K Views

שדות מגנטיים
Physics II
33.6K Views

מטען חשמלי בשדה מגנטי
Physics II
33.7K Views

חוק אוהם לתמי ומנצחים נוהמיים
Physics II
26.3K Views

סדרות ונגדים מקבילים
Physics II
33.2K Views

קיבוליות
Physics II
43.8K Views

אינדוקציה
Physics II
21.6K Views

מעגלי RC/RL/LC
Physics II
143.0K Views

מוליכים למחצה
Physics II
29.9K Views

אפקט פוטואלקטרי
Physics II
32.7K Views

השתקפות ושיפור
Physics II
36.2K Views

הפרעות עקיפה
Physics II
91.3K Views

גלי קול ומשמרת דופלר
Physics II
23.5K Views
Copyright © 2025 MyJoVE Corporation. All rights reserved