A subscription to JoVE is required to view this content. Sign in or start your free trial.

In This Article

  • Summary
  • Abstract
  • Introduction
  • Protocol
  • Results
  • Discussion
  • Disclosures
  • Acknowledgements
  • Materials
  • References
  • Reprints and Permissions

Summary

The goal of this protocol is to reveal structural dynamics of one-dimensional diffusion of protein along DNA, using a plant transcription factor WRKY domain protein as an exemplary system. To do this, both atomistic and coarse-grained molecular dynamics simulations along with extensive computational samplings have been implemented.

Abstract

One-dimensional (1-D) sliding of transcription factor (TF) protein along DNA is essential for facilitated diffusion of the TF to locate target DNA site for genetic regulation. Detecting base-pair (bp) resolution of the TF sliding or stepping on the DNA is still experimentally challenging. We have recently performed all-atom molecular dynamics (MD) simulations capturing spontaneous 1-bp stepping of a small WRKY domain TF protein along DNA. Based on the 10 µs WRKY stepping path obtained from such simulations, the protocol here shows how to conduct more extensive conformational samplings of the TF-DNA systems, by constructing the Markov state model (MSM) for the 1-bp protein stepping, with various numbers of micro- and macro-states tested for the MSM construction. In order to examine processive 1-D diffusional search of the TF protein along DNA with structural basis, the protocol further shows how to conduct coarse-grained (CG) MD simulations to sample long-time scale dynamics of the system. Such CG modeling and simulations are particularly useful to reveal the protein-DNA electrostatic impacts on the processive diffusional motions of the TF protein above tens of microseconds, in comparison with sub-microseconds to microseconds protein stepping motions revealed from the all-atom simulations.

Introduction

Transcription factors (TF) search for the target DNA to bind and regulate gene transcription and related activities1. Aside from the three-dimensional (3D) diffusion, the facilitated diffusion of TF has been suggested to be essential for target DNA search, in which the proteins can also slide or hop along one-dimensional (1D) DNA, or jump with intersegmental transfer on the DNA2,3,4,5,6,7.

In a recent study, we have conducted tens of microseconds (µs) all-atom equilibrium molecular dynamics (MD) simulations on a plant TF - the WRKY domain protein on the DNA8. A complete 1-bp stepping of WRKY on poly-A DNA within microseconds has been captured. The movements of the protein along the DNA groove and hydrogen bonds (HBs) breaking-reforming dynamics have been observed. While such a trajectory represents one sampled path, an overall protein stepping landscape is still lack of. Here, we show how to expand computational samplings around the initially captured protein stepping path with the constructed Markov state model (MSM), which have been implemented widely for simulating a variety of biomolecular systems involving substantial conformational changes and time-scale separation9,10,11,12,13,14,15,16,17,18,19. The purpose is to reveal the conformational ensemble and meta-stable states of the TF protein diffusion along DNA for one cyclic step.

While the above MD simulation reveals atomic resolution of the protein movements for 1 bp on the DNA, the structural dynamics of long-time processive diffusion of the TF along DNA at the same high-resolution is hardly accessible. Conducting coarse-grained (CG) MD simulations at residue level is however technically approachable. The CG simulation time scale can be effectively extended to tens or hundreds of times longer than the atomic simulations20,21,22,23,24,25,26,27,28,29. Here, we show the CG simulations conducted by implementing the CafeMol software developed by Takada lab30.

In current protocol, we present the atomic simulations of the WRKY domain protein along poly-A DNA and the MSM construction first, which focus on sampling the protein stepping motions for only 1 bp along DNA. Then we present the CG modeling and simulations of the same protein-DNA system, which extend the computational sampling to the protein processive diffusion over tens of bps along DNA.

Here, we use GROMACS31,32,33 software to conduct MD simulations and MSMbuilder34 to construct the MSM for sampled conformational snapshots, as well as to use VMD35 to visualize the biomolecules. The protocol requires that the user to be able to install and implement the software above. The installation and implementation of the CafeMol30 software is then necessary for conducting the CG MD simulations. Further analyses of the trajectories and visualization are also conducted in VMD.

Protocol

1. Construction of the Markov state model (MSM) from atomic MD simulations

  1. Spontaneous protein stepping pathway and initial structures collection
    1. Use a previously obtained 10-µs all-atom MD trajectory8 to extract 10000 frames evenly from a "forward" 1-bp stepping path (i.e., one frame for each nanosecond). The total number of frames needs to be sufficiently large to include all representative conformations.
    2. Prepare the transition path with 10000 frames in VMD by clicking File > Save coordinates, type protein or nucleic in selected atoms box and choose frames in Frames box, click Save to get the frames needed.
      NOTE: A previously obtained 10 µs all-atom MD simulation trajectory (called "forward stepping trajectory" here) for WRKY stepping 1-bp distance on a 34-bp homogeneous poly-A DNA8 was used as the initial path to launch further conformational samplings. Note that in most of practices, however, an initial path is constructed, by performing steered or targeted MD simulations, or implementing general path-generation methods, etc.36,37,38,39.
    3. Align the long axis of the reference DNA (from crystal structure) to the x-axis, and set the initial center of mass (COM) of the full 34-bp DNA at the origin of the coordinate space for the convenience of further data analysis. To do this, click Extensions > Tk Console in VMD, and type in the Tk console command window:
      source rotate.tcl
      The tcl script can be found in Supplementary File 3.
    4. Then calculate the root-mean-square-distance (RMSD) of the protein backbone by aligning the central 10 bp DNA (A 14 to 23 and T 14' to 23') to that from the crystal structure40, and the RMSD represent geometrical measures of the systems (see Figure 1A). Do this by clicking VMD > Extensions > Analysis > RMSD trajectory tool and type nucleic and residue 14 to 23 and 46 to 55 in atom selection box, click Align and then RMSD box to calculate the RMSD values.
    5. Calculate the rotational degree of protein around DNA Θ(t) on the y-z plane in MATLAB by typing the command
      rad2deg(atan(z/y))
      with the initial angular positioning defined as Θ(0)=0, as conducted previously8.
    6. Type the following command in MATLAB41 to use K-means methods42,43,44 and classify the 10000 structures into 25 clusters by typing:
      [idx, C]=kmeans( X, 25)
      here X is a 2D matrix of RMSD and rotational angle of WRKY on the DNA. Gather the structures of these 25 cluster centers for further MD simulations.
      NOTE: Since the protein RMSD sampled relative to DNA covers a range of about 25 Å, we choose 25 clusters to have one cluster per angstrom.
  2. Conducting the 1st round of MD simulations and the simulation settings
    1. Build atomistic systems for the 25 structures by using GROMACS 5.1.2 software32 under parmbsc1 force field45 and by using the buildsystem.sh file from Supplementary File 2 in shell.
    2. Conduct 60-ns MD simulations for these 25 systems under NPT ensemble with a time step of 2 fs by typing the following command in shell:
      gmx_mpi grompp -f md.mdp -c npt.gro -p topol.top -o md.tpr
      gmx_mpi mdrun -deffnm md
  3. Clustering the 1st round MD trajectories
    1. Remove the first 10 ns of each simulation trajectory by typing in shell:
      gmx_mpi trjcat -f md.xtc -b 10000 -e 600000 -o newtraj.xtc
      and collect conformations from the 25 × 50 ns trajectories for clustering to prepare the input structures for the subsequent more extensive samplings (2nd round MD simulations).
      NOTE: To reduce the impact from the initial path and to allow local equilibration, 10-ns of the initial period of simulations were removed.
    2. Choose distance pairs between protein and DNA as input parameters for the time-independent component analysis (tICA)46,47,48 projection. Use the make_ndx command in GROMACS to do that:
      gmx_mpi make_ndx -f input.pdb -o index.ndx
      NOTE: Here, the protein CA atoms and the heavy atoms (NH1, NH2, OH, NZ, NE2, ND2) of residue Y119, K122, K125, R131, Y133, Q146, K144, R135, W116, R117, Y134, K118, Q121 that can form hydrogen bonds (HBs) with the DNA nucleotide were selected, which pair with the O1P O2P and N6 atoms of the DNA nucleotide (A14-20, T19-23). The selected amino acids can either form stable HBs or salt bridges with DNA.
    3. Copy the above selected atom index from index.ndx file to a new text file (index.dat). Get the pair information between these atoms by the python script from Supplementary File 1 generate_atom_indices.py and type:
      python2.6 generate_atom_indices.py index.dat > AtomIndices.txt
      This generates the 415 distance pairs between protein and DNA.
    4. Calculate the 415 distance pairs from every trajectory by typing the following command in MSMbuilder command window:
      msmb AtomPairsFeaturizer -out pair_features --pair_indices AtomIndices.txt --top references.pdb --trjs "trajectories/*.xtc" --transformed pair_features --stride 5
    5. Conduct tICA to reduce the dimension of data onto the first 2 time-independent components (tICs) or vectors by typing:
      msmb tICA -i ../tica_rc_a/tmp/ -o tica_results --n_components 2 --lag_time 10 --gamma 0.05 -t tica_results.h5
      NOTE: tICA is a dimension-reduction method that calculates the eigenvalue of time-lagged correlation matrix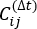 figure-protocol-6427 to determine the slowest relaxing degrees of freedom of the simulation system by the equation:
      figure-protocol-6599
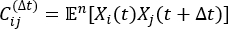
      where Xi(t) is the value of the i-th reaction coordinate at time t, and Xj(t+Δt) is the value of the j-th reaction coordinate at time t+Δt.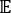 figure-protocol-6920 is the expectation value of the product of the Xi(t) and Xj(t + Δt) overall simulation trajectories. The directions along the slowest relaxing degrees of freedom correspond to the largest eigenvalues of the above time-lagged correlation matrix 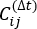figure-protocol-7305. Here, 2 tICs seem to be a minimal set to differentiate three macrostates upon our MSM construction (addressed later). One can also calculate the generalized matrix Rayleigh quotient (GMRQ) score49, for example, to explore an optimal set of components to be used.
    6. Use command in MSMbuilder to cluster the projected datasets into 100 clusters by K-center43,44 method (see Figure 1B):
      msmb KCenters -i ./tica_results.h5 -o kcenters_output -t kcenters_output --n_clusters 100.
      Select the center structure of each cluster as the initial structure for the 2nd round of MD simulations. Maintain the simulation information of the simulated 100 structures, including positions, temperatures, pressures, etc., except for the velocities.
      NOTE: After the first round of 25 simulations, the memory of the initial path has been reduced, so we generate more clusters, e.g., 100 clusters, in the second round, to substantially expand the conformational samplings.
  4. Conducting the 2nd round extensive MD simulations
    1. Conduct 60-ns MD simulations starting from these 100 initial structures after imposing random initial velocities on all the atoms. Add the random initial velocities by turning on the velocity generation in mdp file, i.e., changing the md.mdp file gen_vel = no to gen_vel = yes.
    2. Remove the first 10 ns of each simulation as described in step 1.3.1, collect 2,500,000 snapshots from the 100 × 50 ns trajectories evenly to construct the MSM.
      NOTE: Note that in the later macrostates construction, a small number of off-path states with a particularly low population (~0.2%, on the bottom of X-Θ plane) were found. These off-path states are classified as one macrostate when the total number of macrostates is set as 3 to 6 (Figure 2B). Since such a low population macrostate includes only 3 trajectories, which were removed in the end, the results shown in this protocol were obtained indeed from 97 × 50 ns trajectories, with a total of 2,425,000 frames or snapshots.
  5. Clustering the 2nd round MD trajectories
    1. Conduct tICA for the 2nd round trajectories as done previously. Type in MSMbuilder:
      msmb tICA -i ../tica_rc_a/tmp/ -o tica_results --n_components 2 --lag_time 10 --gamma 0.05 -t tica_results.h5
    2. Calculate the implied timescale to validate parameters for the correlation delay time Δt and microstates numbers (see Figure 1C),
      figure-protocol-10122
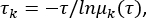
      where τ represents the lag-time used for building the transition probability matrix (TPM); μk(τ) represents the kth eigenvalue of the TPM under a lag time of τ. Use the python script from Supplementary File 1 for this python BuildMSMsAsVaryLagTime.py -d ../ -f ../trajlist_num -i 50 -m 1000 -t 10 -n 20 -s 500.
    3. Vary the lag-time τ and microstates number by changing the parameters used above:
      python BuildMSMsAsVaryLagTime.py -d ../ -f ../trajlist_num -i 50 -m 1000 -t 5 10 20 30 40 -n 20 -s 20 200 400 500 800 2000
      NOTE: The system is regarded as Markovian when the implied timescale curves start to level off with time-scale separation. Then, choose the Dt as the correlation delay time, and the τ the lag time where the implied timescale starts to level off to build MSM.
    4. Accordingly, choose a comparatively large (but not too large) number of states, N = 500, and a comparatively short correlation delay time Δt =10 ns. The lag time was found to be τ =10 ns to build MSM.
    5. Classify the conformations into 500 clusters (see Figure 1D) by using the command:
      msmb KCenters -i ./tica_results.h5 -o kcenters_output -t kcenters_output --n_clusters 500
  6. MSM construction
    1. Lump the 500 microstates into 3–6 macrostates to find out the number of macrostates which suit best according to the PCCA+ algorithm50 in MSMbuilder, by using the python script in Supplementary File 1 python msm_lumping_usingPCCAplus.py. Identify a reduced kinetic network of models for the most essential conformational changes of biomolecules, by constructing a small number of macrostates, i.e., upon kinetically lumping hundreds of microstates as described below17,51.
    2. Map the high-dimensional conformations to the X (protein movement along the DNA long axis) and rotational angle of the protein along the DNA for each macrostate as described in step 1.1.3 and 1.1.4 (e.g., no state with too low population < 1%; see Figure 2C). Then find the 3 macrostates that best represent the system (Figure 1E) . See Figure 2D for snapshots of the movement of protein along DNA and the protein rotation angle around DNA.
      NOTE: In previous work generating the 10 μs spontaneous protein forward stepping path, we additionally conducted 5 x 4 μs equilibrium MD simulations to moderately expand the samplings. We showed the mapping of the original forward path (see Figure 2A left) and further 4-μs sampling trajectories on the forward path conducted previously (see Figure 2A right)8. The mapping of the original 100 × 50 ns (see Figure 2B left)8 and the 97 × 50 ns trajectories used in this work are shown (see Figure 2B right).
  7. Calculation of the mean first passage times (MFPT)
    1. Conduct five 10-ms Monte Carlo (MC) trajectories based on the TPM of the 500 microstate MSM with the lag time of 10 ns set as the time step of MC. Calculate MFPT52 between each pair of macrostates (Figure 3) by the python script in Supplementary File 1 python python mfpt_msm3.py.
    2. Calculate the average and standard error of the MFPT using the bash file in Supplementary File 2, type:
      sh mfpt_analysis.bash

2. Conducting coarse-grained (CG) simulation to sample long-time dynamics

  1. Conduct a CG simulations by using the CafeMol 3.0 software30. See the CG simulation settings specified in the input configuration file with an extension .inp, including input structures, simulation parameters, output files, etc. Type the following command on the terminal to run the CG simulation:
    cafemol XXX.inp
  2. Specify the following blocks in the input file, with each block starting with the label <<<< and ending with >>>>.
    1. Set filenames block (required) to specify the working directories and input/output file store path. Type following for the filenames block for these simulations:
      <<<< filenames
      path = XXXXX (working path)
      filename = wrky (the output file names)
      OUTPUT psf pdb movie dcd rst
      path_pdb = XXXXX (input native structure path)
      path_ini = XXXXX (input initial structure path)
      path_natinfo = XXXXX (native information file path)
      path_para = XXXXX (parameter files path)
      >>>>
      NOTE: As the Go-model53 is utilized in the CG modeling, i.e., protein will be biased to the native conformation, so one needs to set the modeled structure as the native conformation. Here, the input crystal structure was set as the native conformation.
    2. Set the job control block (required) to define the running mode of the simulations. Type the following command:
      <<<< job_cntl
      i_run_mode = 2 (= 2 the constant temperature simulation)
      i_simulate_type = 1 (=1 Langevin dynamics)
      i_initial_state = 2 (=2 means the initial configuration is Native configuration)
      >>>> 
      Select the constant temperature Langevin dynamics simulations.
    3. Set the unit and state block (required) to define the information for input structures. Type the following command:
      <<<< unit_and_state
      i_seq_read_style = 1 (=1 means read sequences from PDB file)
      i_go_native_read_style = 1 (=1 means the native structure is from PDB file)
      1 protein protein.pdb (unit&state molecular_type native_structure)
      2-3 dna DNA.pdb (unit&state molecular_type native_structure)
      >>>>
      NOTE: The initial input structure files (protein.pdb and DNA.pdb here) are needed. The structures are written in the pdb format. Two pdb files are needed here: one is the protein structure file containing the heavy atom coordinates of WRKY (unit 1), and the other is the coordinates of 200-bp double-stranded (ds) DNA (unit 2-3). The protein is initially placed 15 Å away from the DNA.
    4. Set the energy function block (required) defined in the energy_function block. Type the following command:
      <<<< energy_function
      LOCAL(1) L_GO
      LOCAL(2-3) L_DNA2
      NLOCAL(1/1) GO EXV ELE
      NLOCAL(2-3/2-3) ELE DNA
      NLOCAL(1/2-3) EXV ELE
      i_use_atom_protein = 0
      i_use_atom_dna = 0
      i_para_from_ninfo = 1
      i_triple_angle_term = 2
      >>>>
      NOTE: In the CG simulations, the protein is coarse-grained by the Go-model53 with each amino acid represented by a CG particle placed at its Cα position. The protein conformation will be biased then towards the native structure, or crystal structure here, under the Go potential (Figure 4A left). The DNA is described by the 3SPN.2 model54, in which each nucleotide is represented by 3 CG particle S, P, N, which correspond to sugar, phosphate, and nitrogenous base, respectively (Figure 4A right). The electrostatic and vdW interactions are considered between different chains. The electrostatic interactions between protein and DNA in the CG simulation are approximated by the Debye-Hückel potential55. The vdW repulsive energy takes the same form as in the Go model.
    5. Set the md_information block (required) to define the simulation information. Type the following command:
      <<<< md_information
      n_step_sim = 1
      n_tstep(1) = 500000000
      tstep_size = 0.1
      n_step_save = 1000
      n_step_neighbor = 100
      i_com_zeroing = 0
      i_no_trans_rot = 0
      tempk = 300.0
      n_seed = -1
      >>>> 
      The n_tstep is the simulation step. Set the tstep_size as the time length of each MD step, each CG Cafemol time step is about 200 fs30, so each MD step here is 200 × 0.1 fs in principle. Update the neighbor list every 100 MD steps (n_step_neighbor = 100). Set the simulation temperature to 300 K. Control the temperature by employing the velocity-type Verlet algorithm for updating protein structure with the Berendsen thermostat56.
      NOTE: The n_step_sim is the basin number of the Go model based potential, or the local minimal number of the energy curve. A multiple-basin potential allows the protein conformation biased to different conformations so that protein conformation can change from one local minimum to another. Here only the single basin Go model is used, which means only one biased conformation (crystal structure) for protein in the simulations. Meanwhile, since there is no protein-DNA hydrogen bonding interaction, etc. modeled in the CG context, the molecular motions can be sampled even faster, i.e., > 10 times than in the atomic simulations.
    6. Set electrostatic block (required only when electrostatic interaction is used) as the electrostatic interaction is considered among different chains, so use this block to the define the parameters for electrostatic interaction by typing:
      <<<< electrostatic
      cutoff_ele = 10.0
      ionic_strength = 0.15
      >>>>
      Set the Debye length in the electrostatic interaction to 10 Å, corresponding to the solution condition. Set the ionic strength to 0.15 M, as at the physiological condition. 

Results

Rotation-coupled sliding or 1 bp stepping of WRKY from the MSM construction
All protein conformations on the DNA are mapped to the longitudinal movement X and rotation angle of the protein COM along DNA (see Figure 3A). The linear coupling of these two degrees indicates rotation-coupled stepping of the WRKY domain protein on the DNA. The conformations can be further clustered into 3 macrostates (S1, S2, and S3) in the MSM. The forward stepping of WRKY then follows...

Discussion

This work addresses how to conduct structure-based computational simulation and samplings to reveal a transcription factor or TF protein moving along DNA, not only at atomic detail of stepping, but also in the processive diffusion, which is essential for the facilitated diffusion of TF in the DNA target search. To do that, the Markov state model or MSM of a small TF domain protein WRKY stepping for 1-bp along homogeneous poly-A DNA was first constructed, so that an ensemble of protein conformations on the DNA along with ...

Disclosures

The authors have no conflict of interests.

Acknowledgements

This work has been supported by NSFC Grant #11775016 and #11635002. JY has been supported by the CMCF of UCI via NSF DMS 1763272 and the Simons Foundation grant #594598 and start-up fund from UCI. LTD has been supported by Natural Science Foundation of Shanghai #20ZR1425400 and #21JC1403100. We also acknowledge the computational support from the Beijing Computational Science Research Center (CSRC).

Materials

NameCompanyCatalog NumberComments
CafeMolKyoto Universitycoarse-grained (CG) simulations
GROMACSUniversity of Groningen Royal Institute of Technology Uppsala Universitymolecular dynamics simulations software
MatlabMathWorksNumerical calculation software
MSMbuilderStanford Universitybuild MSM
VMDUNIVERSITY OF ILLINOIS AT URBANA-CHAMPAIGNmolecular visualization program

References

  1. Latchman, D. S. Transcription factors: an overview. The International Journal of Biochemistry & Cell Biology. 29 (12), 1305-1312 (1997).
  2. Berg, O. G., von Hippel, P. H. Selection of DNA binding sites by regulatory proteins. Statistical-mechanical theory and application to operators and promoters. Journal of Molecular Biology. 193 (4), 723-750 (1987).
  3. von Hippel, P. H., Berg, O. G. Facilitated target location in biological systems. The Journal of Biological Chemistry. 264 (2), 675-678 (1989).
  4. Halford, S. E., Marko, J. F. How do site-specific DNA-binding proteins find their targets. Nucleic Acids Research. 32 (10), 3040-3052 (2004).
  5. Slusky, M., Mirny, L. A. Kinetics of protein-DNA interaction: facilitated target location in sequence-dependent potential. Biophysical Journal. 87 (6), 4021-4035 (2004).
  6. Bauer, M., Metzler, R. Generalized facilitated diffusion model for DNA-binding proteins with search and recognition states. Biophysical Journal. 102 (10), 2321-2330 (2012).
  7. Shvets, A. A., Kochugaeva, M. P., Kolomeisky, A. B. Mechanisms of Protein Search for Targets on DNA: Theoretical Insights. Molecules. 23 (9), 2106 (2018).
  8. Dai, L., Xu, Y., Du, Z., Su, X. D., Yu, J. Revealing atomic-scale molecular diffusion of a plant-transcription factor WRKY domain protein along DNA. Proceedings of the National Academy of Sciences of the United States of America. 118 (23), 2102621118 (2021).
  9. Chodera, J. D., Singhal, N., Pande, V. S., Dill, K. A., Swope, W. C. Automatic discovery of metastable states for the construction of Markov models of macromolecular conformational dynamics. The Journal of Chemical Physics. 126 (15), 155101 (2007).
  10. Pan, A. C., Roux, B. Building Markov state models along pathways to determine free energies and rates of transitions. The Journal of Chemical Physics. 129 (6), 064107 (2008).
  11. Bowman, G. R., Huang, X., Pande, V. S. Using generalized ensemble simulations and Markov state models to identify conformational states. Methods. 49 (2), 197-201 (2009).
  12. Prinz, J. H., et al. Markov models of molecular kinetics: Generation and validation. The Journal of chemical physics. 134 (17), 174105 (2011).
  13. Chodera, J. D., Noé, F. Markov state models of biomolecular conformational dynamics. Current Opinion in Structural Biology. 25, 135-144 (2014).
  14. Malmstrom, R. D., Lee, C. T., Van Wart, A. T., Amaro, R. E. On the Application of Molecular-Dynamics Based Markov State Models to Functional Proteins. Journal of Chemical Theory and Computation. 10 (7), 2648-2657 (2014).
  15. Husic, B. E., Pande, V. S. Markov State Models: From an Art to a Science. Journal of the American Chemical Society. 140 (7), 2386-2396 (2018).
  16. Sittel, F., Stock, G. Perspective: Identification of collective variables and metastable states of protein dynamics. The Journal of chemical physics. 149 (15), 150901 (2018).
  17. Wang, W., Cao, S., Zhu, L., Huang, X. Constructing Markov State Models to elucidate the functional conformational changes of complex biomolecules. WIREs Computational Molecular Science. 8, 1343 (2018).
  18. Peng, S., et al. Target search and recognition mechanisms of glycosylase AlkD revealed by scanning FRET-FCS and Markov state models. Proceedings of the National Academy of Sciences of the United States of America. 117 (36), 21889-21895 (2020).
  19. Tian, J., Wang, L., Da, L. T. Atomic resolution of short-range sliding dynamics of thymine DNA glycosylase along DNA minor-groove for lesion recognition. Nucleic Acids Research. 49 (3), 1278-1293 (2021).
  20. Chu, J. -. W., Izveko, S., Voth, G. The multiscale challenge for biomolecular systems: coarse-grained modeling. Molecular Simulation. 32 (3-4), 211-218 (2006).
  21. Marrink, S. J., Risselada, H. J., Yefimov, S., Tieleman, D. P., De Vries, A. H. The MARTINI force field: coarse grained model for biomolecular simulations. The Journal of Physical Chemistry B. 111 (27), 7812-7824 (2007).
  22. Givaty, O., Levy, Y. Protein sliding along DNA: dynamics and structural characterization. Journal of Molecular Biology. 385 (4), 1087-1097 (2009).
  23. Khazanov, N., Levy, Y. Sliding of p53 along DNA can be modulated by its oligomeric state and by cross-talks between its constituent domains. Journal of Molecular Biology. 408 (2), 335-355 (2011).
  24. Riniker, S., Allison, J. R., van Gunsteren, W. F. On developing coarse-grained models for biomolecular simulation: a review. Physical Chemistry Chemical Physics : PCCP. 14 (36), 12423-12430 (2012).
  25. Kmiecik, S., et al. Coarse-Grained Protein Models and Their Applications. Chemical Reviews. 116 (14), 7898-7936 (2006).
  26. Bhattacherjee, A., Krepel, D., Levy, Y. Coarse-grained models for studying protein diffusion along DNA. WIREs Computational Molecular Science. 6, 515-531 (2016).
  27. Wang, J., et al. Machine Learning of Coarse-Grained Molecular Dynamics Force Fields. ACS Central Science. 5 (5), 755-767 (2019).
  28. Joshi, S. Y., Deshmukh, S. A. A review of advancements in coarse-grained molecular dynamics simulations. Molecular Simulation. 47 (10-11), 786-803 (2021).
  29. Bigman, L. S., Greenblatt, H. M., Levy, Y. What Are the Molecular Requirements for Protein Sliding along DNA. The Journal of Physical Chemistry B. 125 (12), 3119-3131 (2021).
  30. Kenzaki, H., et al. CafeMol: A Coarse-Grained Biomolecular Simulator for Simulating Proteins at Work. Journal of Chemical Theory and Computation. 7 (6), 1979-1989 (2011).
  31. Berendsen, H. J. C., vander Spoel, D., van Drunen, R. GROMACS: a message-passing parallel molecular dynamics implementation. Computer Physics Communications. 91 (1-3), 43-56 (1995).
  32. vander Spoel, D., et al. GROMACS: fast, flexible, and free. Journal of Computational Chemistry. 26 (16), 1701-1718 (2005).
  33. Abraham, M. J., et al. GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX. 1-2, 19-25 (2015).
  34. Harrigan, M. P., et al. MSMBuilder: Statistical Models for Biomolecular Dynamics. Biophysical journal. 112 (1), 10-15 (2017).
  35. Humphrey, W., Dalke, A., Schulten, K. VMD: visual molecular dynamics. Journal of Molecular Graphics. 14 (1), 33-38 (1996).
  36. Izrailev, S., et al. Steered Molecular Dynamics. Computational Molecular Dynamics: Challenges, Methods, Ideas. 4, 39-65 (1999).
  37. Schlitter, J., Engels, M., Krüger, P. Targeted molecular dynamics: a new approach for searching pathways of conformational transitions. Journal of Molecular Graphics. 12 (2), 84-89 (1994).
  38. Maragliano, L., Fischer, A., Vanden-Eijnden, E., Ciccotti, G. String method in collective variables: minimum free energy paths and isocommittor surfaces. The Journal of Chemical Physics. 125 (2), 24106 (2006).
  39. Weiss, D. R., Levitt, M. Can morphing methods predict intermediate structures. Journal of Molecular Biology. 385 (2), 665-674 (2009).
  40. Xu, Y. P., Xu, H., Wang, B., Su, X. D. Crystal structures of N-terminal WRKY transcription factors and DNA complexes. Protein. 11 (3), 208-213 (2020).
  41. Higham, D. J., Higham, N. J. MATLAB guide. Society for Industrial and Applied Mathematics. , (2016).
  42. Hartigan, J. A., Wong, M. A. Algorithm AS 136: A K-Means Clustering Algorithm. Journal of the Royal Statistical Society. Series C (Applied Statistics). 28 (1), 100-108 (1979).
  43. Gonzalez, T. F. Clustering to minimize the maximum intercluster distance. Theoretical Computer Science. 38, 293-306 (1985).
  44. Zhao, Y., Sheong, F. K., Sun, J., Sander, P., Huang, X. A fast parallel clustering algorithm for molecular simulation trajectories. Journal of Computational Chemistry. 34 (2), 95-104 (2013).
  45. Ivani, I., et al. Parmbsc1: a refined force field for DNA simulations. Nature Methods. 13 (1), 55-58 (2016).
  46. Naritomi, Y., Fuchigami, S. Slow dynamics of a protein backbone in molecular dynamics simulation revealed by time-structure based independent component analysis. The Journal of Chemical Physics. 139 (21), 215102 (2013).
  47. Naritomi, Y., Fuchigami, S. Slow dynamics in protein fluctuations revealed by time-structure based independent component analysis: the case of domain motions. The Journal of Chemical Physics. 134 (6), 065101 (2011).
  48. Pérez-Hernández, G., Paul, F., Giorgino, T., De Fabritiis, G., Noé, F. Identification of slow molecular order parameters for Markov model construction. The Journal of Chemical Physics. 139 (1), 015102 (2013).
  49. McGibbon, R. T., Pande, V. S. Variational cross-validation of slow dynamical modes in molecular kinetics. The Journal of Chemical Physics. 142 (12), 124105 (2015).
  50. Deuflhard, P., Weber, M. Robust Perron cluster analysis in conformation dynamics. Linear Algebra and its Applications. 398, 161-184 (2005).
  51. Silva, D. A., et al. Millisecond dynamics of RNA polymerase II translocation at atomic resolution. Proceedings of the National Academy of Sciences of the United States of America. 111 (21), 7665-7670 (2014).
  52. Swope, W. C., Pitera, J. W., Suits, F. Describing Protein Folding Kinetics by Molecular Dynamics Simulations. 1. Theory. The Journal of Physical Chemistry B. 108 (21), 6571-6581 (2004).
  53. Clementi, C., Nymeyer, H., Onuchic, J. N. Topological and energetic factors: what determines the structural details of the transition state ensemble and "en-route" intermediates for protein folding? An investigation for small globular proteins. Journal of molecular biology. 298 (5), 937-953 (2000).
  54. Hinckley, D. M., Freeman, G. S., Whitmer, J. K., De Pablo, J. J. An experimentally-informed coarse-grained 3-Site-Per-Nucleotide model of DNA: structure, thermodynamics, and dynamics of hybridization. The Journal of chemical physics. 139 (14), 144903 (2013).
  55. Debye, P., Huckel, E. The theory of the electrolyte II-The border law for electrical conductivity. Physikalische Zeitschrift. 24, 305-325 (1923).
  56. Berendsen, H. J., Postma, J. V., van Gunsteren, W. F., DiNola, A., Haak, J. R. Molecular dynamics with coupling to an external bath. The Journal of Chemical Physics. 81, 3684-3690 (1984).
  57. Bowman, G. R. Improved coarse-graining of Markov state models via explicit consideration of statistical uncertainty. The Journal of Chemical Physics. 137 (13), 134111 (2012).
  58. Jain, A., Stock, G. Identifying metastable states of folding proteins. Journal of Chemical Theory and Computation. 8 (10), 3810-3819 (2012).
  59. Röblitz, S., Weber, M. Fuzzy spectral clustering by PCCA+: application to Markov state models and data classification. Advances in Data Analysis and Classification. 7, 147-179 (2013).
  60. Mardt, A., Pasquali, L., Wu, H., Noé, F. VAMPnets for deep learning of molecular kinetics. Nature Communications. 9 (1), 5 (2018).
  61. Wang, W., Liang, T., Sheong, F. K., Fan, X., Huang, X. An efficient Bayesian kinetic lumping algorithm to identify metastable conformational states via Gibbs sampling. The Journal of Chemical Physics. 149 (7), 072337 (2018).
  62. Chen, W., Sidky, H., Ferguson, A. L. Nonlinear discovery of slow molecular modes using state-free reversible VAMPnets. The Journal of Chemical Physics. 150 (21), 214114 (2019).
  63. Gu, H., et al. RPnet: a reverse-projection-based neural network for coarse-graining metastable conformational states for protein dynamics. Physical Chemistry Chemical Physics :PCCP. 24 (3), 1462-1474 (2022).
  64. Lane, T. J., Bowman, G. R., Beauchamp, K., Voelz, V. A., Pande, V. S. Markov state model reveals folding and functional dynamics in ultra-long MD trajectories. Journal of the American Chemical Society. 133 (45), 18413-18419 (2011).
  65. Konovalov, K. A., Unarta, I. C., Cao, S., Goonetilleke, E. C., Huang, X. Markov State Models to Study the Functional Dynamics of Proteins in the Wake of Machine Learning. JACS Au. 1 (9), 1330-1341 (2021).
  66. Cao, S., Montoya-Castillo, A., Wang, W., Markland, T. E., Huang, X. On the advantages of exploiting memory in Markov state models for biomolecular dynamics. The Journal of Chemical Physics. 153 (1), 014105 (2020).
  67. Brandani, G. B., Takada, S. Chromatin remodelers couple inchworm motion with twist-defect formation to slide nucleosomal DNA. PLoS Computational Biology. 14 (11), 1006512 (2018).
  68. Tan, C., Terakawa, T., Takada, S. Dynamic Coupling among Protein Binding, Sliding, and DNA Bending Revealed by Molecular Dynamics. Journal of the American Chemical Society. 138 (27), 8512-8522 (2016).
  69. Terakawa, T., Takada, S. p53 dynamics upon response element recognition explored by molecular simulations. Scientific reports. 5, 17107 (2015).
  70. Brandani, G. B., Niina, T., Tan, C., Takada, S. DNA sliding in nucleosomes via twist defect propagation revealed by molecular simulations. Nucleic Acids Research. 46 (6), 2788-2801 (2018).
  71. Knotts, T. A., Rathore, N., Schwartz, D. C., de Pablo, J. J. A coarse grain model for DNA. The Journal of Chemical Physics. 126 (8), 084901 (2007).
  72. Freeman, G. S., Hinckley, D. M., Lequieu, J. P., Whitmer, J. K., de Pablo, J. J. Coarse-grained modeling of DNA curvature. The Journal of Chemical Physics. 141 (16), 165103 (2014).

Reprints and Permissions

Request permission to reuse the text or figures of this JoVE article

Request Permission

Explore More Articles

Transcription FactorProtein MovementsDNA DiffusionAtomic scale SimulationCoarse grained SimulationWRKY DomainMarkov State ModelMD TrajectoryVMD SoftwareRMSD TrajectoryAngular PositioningK means ClusteringGROMACSNPT EnsembleTime independent Component Analysis

This article has been published

Video Coming Soon

JoVE Logo

Privacy

Terms of Use

Policies

Contact Us

Recommend to library

JoVE NEWSLETTERS

Research

Education

Authors

Librarians

ABOUT JoVE

Copyright © 2025 MyJoVE Corporation. All rights reserved