Multiplex Chemical Imaging Based on Broadband Stimulated Raman Scattering Microscopy
In This Article
Summary
We present a protocol to acquire chemical images with broadband stimulated Raman scattering (SRS) microscopy. Based on an SRS microscope that operates with differential multichannel-lock-in detection, the protocol describes the sample preparation, adjustment of the SRS apparatus, and chemometrics to disentangle different constituents of chemically heterogeneous samples.
Abstract
Stimulated Raman scattering (SRS) microscopy is a nonlinear optical technique for label-free chemical imaging. This analytical tool delivers chemical maps at high speed, and high spatial resolution of thin samples by directly interrogating their molecular vibrations. In its standard implementation, SRS microscopy is narrowband and forms images with only a single vibrational frequency at a time. However, this approach not only hinders the chemical specificity of SRS but also neglects the wealth of information encoded within vibrational spectra.
These limitations can be overcome by broadband SRS, an implementation capable of extracting a vibrational spectrum per pixel of the image in parallel. This delivers hyperspectral data that, when coupled with chemometric analysis, maximizes the amount of information retrieved from the specimen. Thus, broadband SRS improves the chemical specificity of the system, allowing the quantitative determination of the concentration of the different constituents of a sample. Here, we report a protocol for chemical imaging with broadband SRS microscopy, based on a home-built SRS microscope operating with a custom differential multichannel-lock-in amplifier detection. It discusses the sample preparation, alignment of the SRS apparatus, and chemometric analysis. By acquiring vibrational Raman spectra, the protocol illustrates how to identify different chemical species within a mixture, determining their relative concentrations.
Introduction
Raman microscopy is a powerful imaging technique that delivers rich chemical maps by measuring Raman scattering1, an inelastic radiative process that originates from molecules vibrating in response to incident light2,3. Each pixel of a Raman map contains a spectrum that carries direct information on the chemical composition and structure of the sample, resulting in images with intrinsic vibrational contrast. To date, Raman microscopy is the reference standpoint for microspectroscopy studies of molecular vibrations as no other imaging technique can produce images with both high chemical specificity and high spatial resolution4. Despite its outstanding chemical specificity, the generation efficiency of Raman scattering is low, calling for either extended pixel dwell times or high-power excitation, leading, respectively, to low acquisition rates and incompatibility with sensitive samples.
This single deficiency of Raman microscopy led researchers to apply coherent Raman scattering5,6,7,8,9 as a source of contrast for microscopy. This is a nonlinear optical process that enhances the vibrational response by several (up to seven) orders of magnitude, thus allowing high-speed chemical imaging10,11,12,13. In particular, the two most employed coherent Raman scattering techniques are coherent anti-Stokes Raman scattering (CARS)14 and stimulated Raman scattering (SRS)15. In contrast to CARS, SRS shows a linear dependence on the concentration of resonant molecules. It is immune to the nonresonant background, a nonlinear effect unrelated to any vibrational transition but distortive to the Lorentzian shapes characteristic of the Raman spectra of the molecular vibrations16,17. Thus, SRS microscopy yields authentic Raman information that allows direct quantitative image analysis.
SRS is a third-order, nonlinear, optical process that provides direct information on the chemical bonds of a sample. It originates from the spatiotemporal superposition of two optical fields generally in the near-infrared spectral region, namely the pump and the Stokes at frequency ωpu and ωS, respectively10,11,18. This superposition generates a beating at the pump-Stokes frequency detuning Ω = ωpu-ωS. When Ω matches a molecular vibration ΩR, the molecule resonates, causing a coherent energy transfer between the light fields and the molecule. As a result, the molecule reaches a vibrationally excited state. This process can be monitored by measuring either the annihilation of pump photons (a signal known as stimulated Raman loss [SRL]) or the concomitant amplification of Stokes photons (a process known as stimulated Raman gain [SRG]). SRG and SRL are small signals (ΔI) that sit on top of an intense and fluctuating background (I). As typical values of the SRS signal (ΔI/I) are in the 10-6-10-4 range, the laser noise can easily obscure it. To mitigate the detrimental effects of the laser noise on the signal-to-noise ratio (SNR) and consequently on the imaging speed, SRS detection relies on modulation transfer techniques (e.g., lock-in amplifiers, resonant circuits, or box-car averagers) at high modulation frequencies (>1 MHz), where the laser noise reaches its minimum values15,19,20.
Conventional SRS microscopy employs narrowband (≈10 cm−1) pump and Stokes pulses to produce chemical images at a single vibrational frequency, allowing video-rate imaging with pixel dwell times as low as ≈100 ns21,22. However, because narrowband SRS microscopy forms chemical maps by sequentially scanning the sample at only a few vibrational frequencies, its information is limited23. SRS images with one or two vibrational contrasts may not suffice to differentiate chemical species with overlapping Raman bands, especially within heterogeneous systems. Therefore, the paradigmatic narrowband SRS microscope does not exploit the full potential of SRS, because investigating a handful of vibrational frequencies hinders its chemical specificity and neglects the wealth of information encoded within vibrational spectra. Furthermore, sequential scanning of the sample at different frequencies results in extended pixel dwell times that can trigger photodamage and prevent rigorous spatial coregistration between consecutive images, leading to motion artifacts.
Contrary to its narrowband counterpart, broadband SRS microscopy retrieves a vibrational spectrum per pixel at each sample scan10,12,24. Thus, broadband SRS provides hyperspectral imaging with strict spatial coregistration of different vibrational contrasts, allowing rigorous data analysis. This not only reveals the chemical constituents of the specimen through Raman spectra, but also helps to determine their relative concentrations. Depending on how the spectra are acquired, broadband SRS microscopy is classified either as hyperspectral SRS or multiplex SRS. In hyperspectral SRS, the SRS spectrum per scanned point of the sample is acquired sequentially (i.e., it is retrieved by sweeping the frequency detuning Ω), building an SRS spectrum by stacking together the SRS signals at consecutive Raman shifts. The Raman spectrum is measured simultaneously at several vibrational modes in multiplex SRS. Thus, the multiplex SRS approach combines a modulated narrowband pulse with a broadband pulse to drive the SRS signal at different frequencies, and uses a multichannel detector with a sensitivity comparable to that of narrowband SRS to detect the SRS spectra.
This paper presents a protocol to produce chemical maps of heterogeneous samples using multiplex SRS microscopy. A scheme of the SRS microscope employed in this protocol is depicted in Figure 1 and described in detail elsewhere25,26,27. Briefly, a commercial mode-locked Yb fiber laser, producing 140 fs pulses centered at 1040 nm, with 10 W average power and an 80 MHz repetition rate, drives the broadband SRS microscope. A polarizing beam splitter (PBS) separates the fundamental beam into two branches. To produce the narrowband Stokes pulses, one branch with 4 W of the fundamental beam is sent to an etalon that generates a narrowband (≈15 cm-1) beam, which is then modulated at 1.6 MHz with an acoustic optic modulator (AOM). The remaining fraction with 6 W of the fundamental beam is frequency-doubled with a 2.8 mm thick lithium triborate (LBO) crystal, cut for type-I phase matching (θ = 90°, φ = 13.8°). The resulting second harmonic generation at 520 nm travels to an X-folded cavity to pump an optical parametric oscillator (OPO), a device that uses a 3.0 mm thick LBO crystal (type I phase matching, θ = 90°, φ = 9.8°) as active medium to deliver a broadband optical radiation tunable within the 680-910 nm spectral region (Figure 2). These broadband pulses serve as the pump in the SRS experiments and propagate to a prism compressor to precompensate the dispersion effects induced by the microscope objective.
After the compression stage, a λ/2 waveplate, combined with a YVO4 birefringent plate, produces two orthogonally polarized replicas whose electronic subtraction at the detection plane cancels the noise of the broadband pump. A dichroic mirror combines the pump and Stokes beams and sends them to an upright microscope. A water-immersion objective with a numerical aperture (NA) of 1.27 focuses the light onto the sample, while an oil-immersion objective with a NA of 1.4 collects it. Before the detection stage, a short-pass filter (SPF) removes the modulated Stokes, while a diffraction grating operating in Littrow configuration disperses the transmitted broadband pump. A second PBS2 separates the pump replicas, and a lens focuses them onto two photodiode arrays. The signals from these photodiode arrays are electronically subtracted and sent to a home-built multichannel-lock-in amplifier (M-LIA). The demodulated signal is then normalized by the direct current (DC) readings of one of the photodiode arrays, thus producing the SRL spectrum.
As an exemplary experiment, we image mixtures of several well-known Raman scatterers, each with a unique Raman spectrum. Thus, the protocol starts by describing how to prepare the reference samples. As we detect SRL, we continue to explain how to obtain narrowband Stokes pulses and set up the optical source that delivers the broadband (≈250 cm-1) pump pulses, namely, the homebuilt OPO. The protocol shows the alignment and optimization of the optical beams, describing critical parameters such as the power and spectra of the narrowband Stokes and the broadband pump. The protocol describes in detail the optical path of the broadband pump because it requires special optical elements. It also explains how to find the spatiotemporal overlap between pump-Stokes pulses and shows a practical way to determine the relative intensity noise (RIN), which in turn helps define the best modulation frequency for SRS experiments. Then, we explain the working principle and calibration of the detection chain. Finally, the protocol shows the data acquisition process, chemometrics, and image processing pipeline.
Protocol
1. Sample preparation
NOTE: This protocol describes the retrieval of the concentration maps and characteristic SRS spectra of chemically heterogeneous mixtures.
- To prepare the sample, extract 2 µL from an aqueous suspension of polymethyl methacrylate (PMMA) microbeads (see the Table of Materials) and pour the 2 µL fraction onto a microscope coverslip.
- With a clean pipette tip, extract 2 µL from an aqueous suspension of polystyrene (PS) microbeads and combine it with the PMMA suspension on the coverslip. Using a pipette tip, gently mix the suspension and let it dry for 24 h.
NOTE: It is important to carefully match the concentration of the microbead suspensions to avoid disproportionate amounts of the microbeads on the sample surface. The diameter of the PS and PMMA beads are 10 and 6 µm, respectively. These dimensions allow demonstrating the high spatial resolution of the microscope without compromising the generation efficiency of SRS.
- With a clean pipette tip, extract 2 µL from an aqueous suspension of polystyrene (PS) microbeads and combine it with the PMMA suspension on the coverslip. Using a pipette tip, gently mix the suspension and let it dry for 24 h.
- On top of the flat, white layer of beads that will appear when the water dries off, add 20 µL of dimethyl sulfoxide (DMSO) and then 20 µL of pure olive oil.
- Apply nail polish on the edges of a second microscope coverslip. Place the coverslip on the mixture, with the nail polish facing down, applying enough pressure to seal it. Let it dry.
NOTE: Figure 3 shows exemplary results obtained with these steps. If properly sealed, this sample should last up to three months.
2. Optimizing pump and Stokes beams
- Switch on the laser, and let it reach thermal equilibrium. Apply a negative group delay dispersion (GDD) of GDD = -6,000 fs2 to the fundamental beam.
NOTE: This GDD value is critical for successfully driving the OPO and is optimal for this setup but will likely vary in different systems. Negative GDD can be introduced through grating pairs, prism compressors, or pulse shapers based on spatial light modulators28. - Split the fundamental laser with a polarizing beamsplitter (PBS1) into two branches. To get the narrowband Stokes pulses, guide one branch with 4 W to an etalon. Slightly rotate the etalon until a narrow spectral line is obtained and centered at the peak of the pulse spectrum (see the red curve in Figure 2).
NOTE: This etalon has an effective finesse of 29 and a free-spectral range of 29.8 nm at 1,040 nm. - To obtain modulated Stokes pulses, send the narrowband beam to an acousto -optical modulator.
NOTE: As shown in Figure 4A, the first-order diffracted beam experiences 100% modulation, while the zeroth-order only 50%. Therefore, it is preferable to employ the first-order to avoid illuminating the sample with a strong unmodulated beam that may induce sample photodamage without generating any SRS signal.- To optimize the modulation efficiency, change the distance between lenses f1 and f2 (Figure 4B). Measure the modulated beam with a photodiode and record its profile with an oscilloscope.
- Change the distance between f1 and f2 until maximum contrast is achieved between the amplitude and the baseline of the oscilloscope readings.
NOTE: This pair of lenses does not operate as a collimator, but rather it creates an effective focal spot at the crystal of the AOM. - Place a third lens f3 to finetune the waist of the Stokes beam, allowing the interaction volume at the focal plane of the microscope to be changed and, consequently, to optimize the SRS signal.
NOTE: The Stokes beam was modulated at 1.6 MHz in this protocol.
- Focus the remaining 6 W of the optical power of the fundamental beam onto a lithium triborate (LBO) crystal (LBO1, θ = 90°, φ = 13.8°) to frequency-double the fundamental beam through second harmonic generation (SHG) (Figure 5A).
- To maximize the SHG efficiency, slightly rotate the crystal, varying the φ angle (Figure 5B). Optimize LBO1 to get at least 2.5 W of SHG.
- Adjust the φ angle of LBO2 to maximize the generation efficiency of the signal beam.
NOTE: The focal lengths of lenses f1, f2, and f3 were carefully chosen to mode-match the SHG beam with the OPO cavity. Thus, the focal lengths of these lenses will vary in different setups. Because of the residual dispersion in the OPO cavity, a slight change in the cavity length induces a shift of the spectrum of the signal beam.- Adjust the cavity length to get a pump spectrum that, together with the narrowband Stokes at 1,040 nm, can produce a frequency detuning within 1,373-5,090 cm-1. This range covers the vibrations in the CH stretching spectral region (2,800-3,050 cm-1). See the blue spectra in Figure 2.
- To compensate for the dispersion effects induced by the excitation microscope objective, send the broadband pump to a prism compressor. Enter the pump into prism A through its apex and guide the dispersed pump toward the apex of prism B. Define the amount of negative dispersion necessary, and then set the distance between the prisms' apices L accordingly.
NOTE: Figure 6 shows the arrangement of the prisms29. In this case, the compensation was set for GDD ≈ -12,800 fs2; hence L = 1.26 m.- Use Brewster-cut prisms.
- Ensure that the polarization of the pump beam lies within the triangular planes of the prisms (top/bottom unpolished faces).
- Ensure that the incidence angle θin of the pump beam matches the Brewster-angle.
- Ensure that the exit face of prism A is parallel to the entrance face of prism B.
- To estimate the GDD of the broadband pulse to be compensated, measure the SRS signal at a single wavelength λ1, recording the time delay τ1 between pump-Stokes at which the maximum SRS(λ1) is obtained. Repeat this procedure for a second wavelength λ2, again registering the time delay τ2 at which the SRS(λ2) was maximum.
NOTE: Because the GDD is defined as the derivative of the group delay with respect to the angular frequency, the aforementioned measurements allow the estimation of the GDD of the broadband beam (Eq [1]).
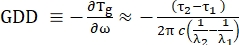 (1)
(1)
- Use Brewster-cut prisms.
- Using a λ/2 waveplate, set the polarization of the pump beam to 45°. Guide the polarized pump to a YVO4 plate with a length of 13.3 mm, setting the fast axis of this birefringent crystal vertical.
NOTE: Upon traveling through the YVO4 plate, the pump pulses will be split into two orthogonally polarized replicas propagating collinearly but keeping a delay Δt ≈ 10 ps between them. This delay is a function of the thickness and the refractive indexes of the birefringent crystal. Hereafter, the pump replicas with the same polarization state of the Stokes pulses will be called "signal" while those with an orthogonal state as "reference". The details of this technique, called inline balanced detection, have been described previously30. - Combine the pump and Stokes beams with a dichroic mirror and carefully align them using a pair of fluorescent pinholes, ensuring that both propagate collinearly. Attenuate the beams and use a lens to focus them onto a fast (at least 100 MHz bandwidth) photodiode.
- Block the pump and measure single Stokes pulses with a high-bandwidth digital oscilloscope. Use the trigger signal of the laser as the clock source for the measurements of the oscilloscope. Determine the mean value at which the photodiode voltage reaches its maximum.
- Block the Stokes beam and repeat this procedure for the pump pulses. Increase or reduce the optical path of the pump (Stokes) beam until its pulses arrive roughly at the same time as the Stokes (pump) pulses.
NOTE: This should guarantee a precision of a few millimeters at maximum in the matching of the optical path difference between the two arms. - Remove the photodiode and place a nonlinear crystal with a suitable cut angle for sum-frequency generation (SFG) between pump-Stokes photons.
NOTE: The nonlinear crystal used here was cut for type I phase matching, θ = 90°, φ = 9.8°. The optical axis of the nonlinear crystal should be parallel to the polarization of the Stokes and signal pulses. - Make the pump/Stokes beams slightly noncollinear and move the delay line until the SFG, a signal that, due to phase matching, is between the SHGs of the pump and Stokes beams. If the signal is not found, verify the spatial overlap of the two beams on the crystal.
NOTE: The SFG is blue-shifted and should be readily visible to the naked eye. - In case of unexpected difficulties, place a low pass filter to remove the pump and Stokes and their respective SHGs and measure the SFG with a spectrometer (Figure 7A). Find the time delay at which the SFG reaches its maximum intensity, a value that determines the ideal spatiotemporal overlap required for nonlinear signal generation, and fix the delay line there (Figure 7B).
- Measure the beam profiles with a calibrated camera. Alternatively, use an infrared card and estimate the diameters by eye. Use two telescopes, one for the pump and another for the Stokes beam. With these telescopes, try to match the beam diameters to the back aperture of the excitation objective.
NOTE: This procedure will guarantee the maximum spatial resolution of the setup.- Once the SRS signal is obtained, use the telescope on the pump beam to tweak its diameter, varying its Rayleigh range and, consequently, the interaction volume at the focus of the microscope. Stop when the maximum SRS is achieved.
- Use a photodiode to measure the intensity of the pump (Stokes) beam and, with the photodiode's responsivity, calculate the mean power
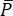 impinging on the active area of the detector.
impinging on the active area of the detector.
- If using a high bandwidth photodiode, connect an electronic low-pass filter to get only the constant or DC component. To measure δP(f), connect the output of a high bandwidth photodiode (disconnect the low pass filter) to the input of a lock-in amplifier. Store the lock-in output in
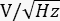 at different demodulation frequencies, and use the responsivity of the photodiode to convert from V to W.
at different demodulation frequencies, and use the responsivity of the photodiode to convert from V to W.
NOTE: Commercial lock-in amplifiers have built-in tools to measure δP(f) (e.g., Zurich Instruments incorporated to LabOne a Frequency Sweeper31). - After measuring the RIN of the beams, switch the laser off and measure the electronic noise (i.e., the RIN calculated without any light on detectors).
NOTE: Provided that the RIN is limited by the laser fluctuations and not by the shot-noise, this dark measurement will help diagnose the instrumentation employed for the measurements; if the electronic noise is as high as the RIN of the laser, this cannot be used to measure the RIN of the laser; ultralow-noise-amplifiers may have to be used to reduce the electronic noise. - If the RIN is limited by the shot-noise and not by the laser fluctuation, shine more optical power onto the detector. See Figure 8.
- If using a high bandwidth photodiode, connect an electronic low-pass filter to get only the constant or DC component. To measure δP(f), connect the output of a high bandwidth photodiode (disconnect the low pass filter) to the input of a lock-in amplifier. Store the lock-in output in
3. Setting up the spectral detection for SRS imaging
- Guide the pump and Stokes beams to the microscope.
- Place the sample discussed in section 1, and find a region without beads to help align the pump beam.Using a camera, measure the reflected profile of the Stokes (pump) beam while blocking the pump (Stokes). Adjust the positions of the laser spots with the mirrors right before the microscope.
NOTE: To get the highest SRS generation, they should perfectly overlap. Figure 9 shows (A) the pump, (B) Stokes, and (C) both beams perfectly overlapped at the focal plane of the microscope. - Make the excitation and collection objectives confocal.
NOTE: The use of infinity-corrected objectives means that focusing the pump on the sample plane will result in a collimated beam at the back aperture of the collection objective.- Put a short-pass filter to remove the modulated Stokes and guide the pump beam to the grating. Place a lens after the grating to focus the dispersed beam onto the detectors.
NOTE: The grating equation will help determine the linear dispersion (i.e., how many nm per mm at the detector plane with a lens of a given focal length f32). The grating equation relates the groove periodicity d of the grating, the angle of incidence α, the diffraction angle β, the diffracted wavelength λ, and diffraction order m (Eq [2]).
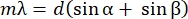 (2)
(2)
- Put a short-pass filter to remove the modulated Stokes and guide the pump beam to the grating. Place a lens after the grating to focus the dispersed beam onto the detectors.
- For balanced detection, measure the spectrum of the reference and the signal replicas propagating along the pump beam.
NOTE: The spatial profile of the pump beam after the grating is a line comprising the different spectral components of the broadband pump along its length. Each spectral component of the pump line will be focused at distance f by a spherical lens (see steps 3.1-3.2).- To avoid clipping the dispersed pump, place the spherical lens as close as possible to the grating. Put a PBS right after the spherical lens to separate the pump replicas.
NOTE: Here, a polarizing cube beam splitter was used because this kind of polarizer does not scramble the polarization of the pump beam. It also effectively separates the different pump replicas and can be large enough to avoid clipping the broadband pump. The PBS will reflect the signal replica (s-polarized) and transmit the reference replica (p-polarized). - With a pair of steering mirrors, guide the signal and reference to their respective detectors (Figure 1).
NOTE: In the ideal balanced configuration, the signal and reference replicas should have the same optical power. - To remove the noise in the pump beam, correlate the channels of the photodiode array measuring the signal with their counterparts in the reference detector. Hence, ensure that the nth photodiode of the signal and reference photodiode arrays measure the optical power of the same spectral component of the signal and reference replicas.
NOTE: Figure 8 shows exemplary RIN spectra.
- To avoid clipping the dispersed pump, place the spherical lens as close as possible to the grating. Put a PBS right after the spherical lens to separate the pump replicas.
- To guarantee the spectral matching between the two photodiode arrays, place a small slit or an iris between the grating and the PBS to spatially filter the dispersed pump. Clip all but one spectral component of the pump replicas to center the transmitted rays on the nth detector of the reference and signal photodiode arrays. Use the mentioned steering mirrors to adjust the correlation of the different detection channels.
- At this point, start SRS microscopy. To do this, modulate the Stokes, raster-scan the sample, and acquire the modulation transfer on the pump spectrum (ΔI) with its corresponding DC spectrum (I) to get the normalized SRS (ΔI/I) spectrum from each pixel. Produce three-dimensional matrices whose rows (x) and columns (y) contain the scanned positions of the sample. On each vector (z) orthogonal to the x-y plane, store an SRS spectrum.
NOTE: Figure 12 shows the structure of SRS hyperspectral data.- Set the power of the Stokes beam to 65 mW and that of the broadband pump beam to 20 mW. Set an ideal integration time for the experiments.
NOTE: Here, the integration time was 44 µs; however, the pixel dwell time was 1 ms due to the slow piezo scanner.
- Set the power of the Stokes beam to 65 mW and that of the broadband pump beam to 20 mW. Set an ideal integration time for the experiments.
4. Chemometrics of hyperspectral SRS data
- Use multivariate curve resolution analysis to disentangle the different chemical constituents of the sample. Download the GUI from the link in Tauler, de Juan, and Jaumot33.
NOTE: Here, Multivariate Curve Resolution-Alternating Least Squares (MCR-ALS) MATLAB program developed by Tauler and coworkers was used34,35. For applications of MCR-ALS to SRS data, refer to 36,37; for detailed discussions on the algorithm, refer to 38. - In MATLAB, reshape the SRS hyperspectral data cube into a matrix D with its rows containing the SRS spectra. Assume that the unfolded SRL hypercube D is a linear combination of the concentration C and the spectral profiles S of the chemical constituents of the sample (i.e., D = CS T + E, where E is a matrix that contains the experimental error, and the superscript T indicates matrix transpose).
- Obtain the main components of the data to separate C and S. As it is known a priori that the sample discussed in section 1 contains four species, namely DMSO, Olive oil, PMMA, and PS, configure the program to search for four species plus another one to account for the background noise. If there is a different sample with a higher or lower number of species, configure the program accordingly.
NOTE: The program makes a singular-value decomposition of the spectral data, using them as the initial guesses of the pure spectra S.- Alternatively, feed the program with a matrix containing the known spectral traces (e.g., the spontaneous Raman spectra of the substances).
NOTE: Using the initial estimates of the pure spectra, the program will calculate C = DS(STS)−1 and ST = (CTC)−1CTD. The new values of C and S are optimized with an alternating least-squares algorithm.
- Alternatively, feed the program with a matrix containing the known spectral traces (e.g., the spontaneous Raman spectra of the substances).
- As SRS is a nonnegative signal, constrain the alternating least-squares algorithm to deliver just positive values.
NOTE: The optimized C and S will allow constructing a new matrix D*= CST, a data set that the program will compare against the original data D. The program automatically iterates these steps until the difference between D* and D is less than an arbitrary threshold value that can be defined. - Plot C and S to acquire chemical images and the characteristic spectra of the chemical constituents of the sample.
Representative Results
Figure 3 shows exemplary results obtained using this protocol with PS, PMMA, and olive oil. This rotation of LBO1 will change the refractive index experienced by the SHG field, directly modifying its phase velocity. When the phase velocity of the SHG field matches that of the nonlinear polarization induced in LBO1, the nonlinearly generated field and the nonlinear polarization will be in phase, leading to intense SHG radiation. In other words, tweaking the φ angle of LBO1 will allow the user to attain the ideal phase matching condition for SHG. As a Type I phase matching crystal is used here, the polarization of the SHG beam will be orthogonal to that of the fundamental beam (Figure 5B).
Figure 8 shows the RIN of the optical sources used in this protocol and the shot-noise limit, which is a consequence of the quantum nature of electrons and photons that sets a fundamental limit to the laser noise. The shot-noise limited RIN is computed with 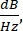 as shown by Eq (3).
as shown by Eq (3).
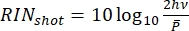 (3)
(3)
Where h is Planck's constant, and ν is the optical frequency. Thus, the shot noise provides useful guidelines for the electronics design.
Figure 11A and Figure 11C show exemplary data of balanced and unbalanced spectra. Naturally, the effects of balanced detection impact the final results of the experiments, namely, the chemical maps. Figure 11B and Figure 11D show composite images in the unbalanced and balanced conditions, respectively. Successfully implementing the described protocol will help identify and localize the different chemical constituents of a heterogeneous sample and extract their characteristic SRS spectra. Subjecting the hyperspectral data of Figure 12 to chemometric analysis gives Figure 13. Figure 13A shows a composite of the concentration maps of the different chemical constituents of the sample, while Figure 13B shows their characteristic SRS spectra. Note that the data shown in Figure 13A not only allows the user to easily identify the different constituents of the sample but also to perform more quantitative analysis. For example, by using the concentration maps, we could calculate the mean of the fractional concentration of each chemical species: 38% DMSO, 25% PMMA, 14% PS, and 22% Olive oil.

Figure 1: Schematic of the broadband SRS microscope employed in this protocol. Abbreviations: PBSx = polarizing beamsplitter; SHG = second harmonic generation module; OPO = optical parametric oscillator; AOM = acousto optic modulator; SPF = short-pass filter; M-LIA: Multichannel lock-in amplifier; DM = dichroic mirror. Please click here to view a larger version of this figure.
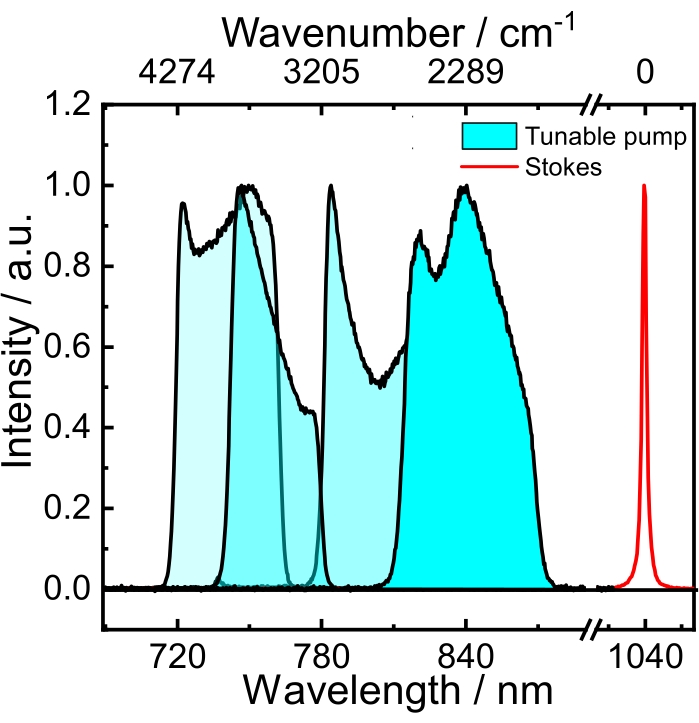
Figure 2: Spectra of the tunable broadband pump (blue) and the narrowband (red) Stokes beams. Please click here to view a larger version of this figure.

Figure 3: Brightfield image of the chemically heterogeneous sample. Note that conventional microscopy does not allow the different constituents to be distinguished. Scale bar = 100 µm. Abbreviations: PS = polystyrene; PMMA = polymethyl methacrylate; DMSO = dimethyl sulfoxide. Please click here to view a larger version of this figure.
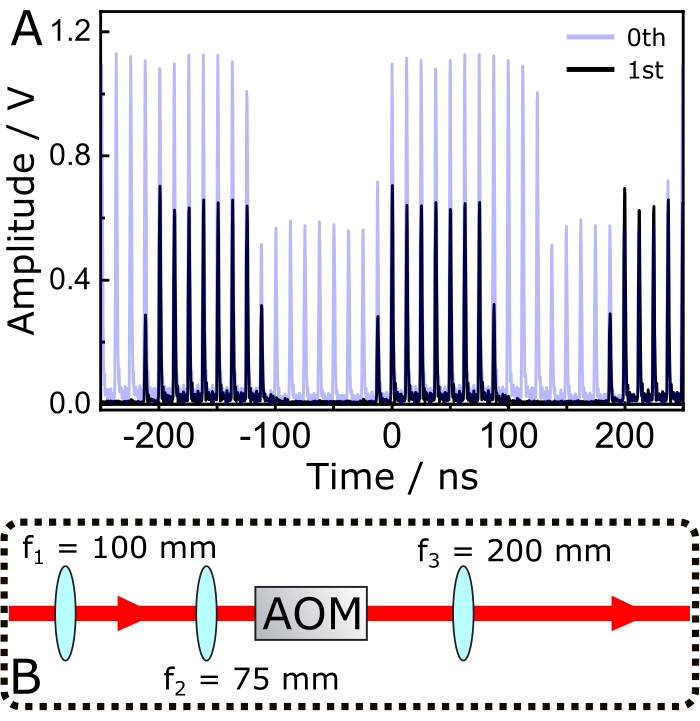
Figure 4: Modulation of the narrowband Stokes pulses. (A) The transparent blue trace shows the 0th diffracted beam, while the black one shows the corresponding 1st order. (B) Optical setup for optimizing the modulation efficiency of the 1st order diffracted beam and finetuning of the Stokes beam's spot size prior to arriving at the excitation objective. Abbreviations: AOM = acousto optic modulator; fx = focal length of lens X. Please click here to view a larger version of this figure.
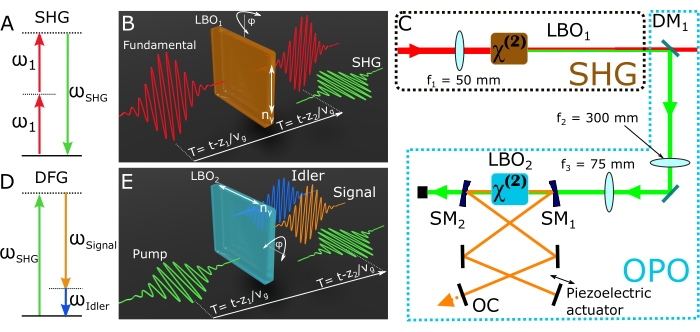
Figure 5: Nonlinear optical processes required to drive the OPO. (A) Geometry of the SHG interaction. Two fundamental photons at ω1 bring the material system to a high-energy virtual level, from where the material system leaps down to the ground state, emitting a photon at ωSHG. (B) Scheme of the SHG experiment. (C) A schematic of the SHG and OPO setups. (D) Geometry of the DFG interaction. A ωSHG photon is split into the signal (ωSignal) and idler (ωIdler) photons. A gain of the signal beam is achieved by feeding back the signal photons and making them resonate in the cavity. (E) Scheme of the DFG experiment. Abbreviations: SMx = spherical mirror (R = 75 mm); OPO = optical parametric oscillator; SHG = second harmonic generation module; DFG = difference-frequency generation; LBO = lithium triborate; OC = oil condenser; DM = dichroic mirror; fx = focal length of lens X. Please click here to view a larger version of this figure.
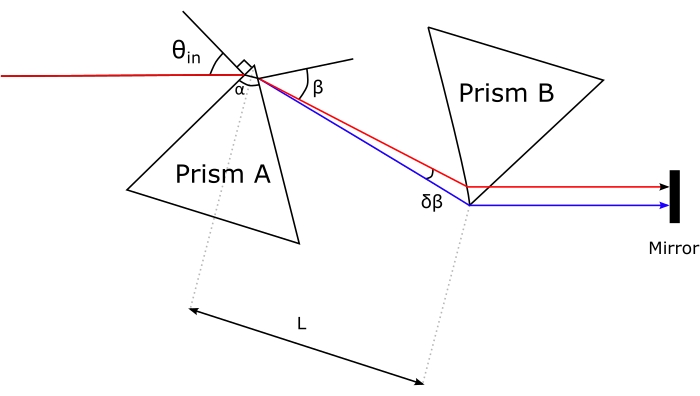
Figure 6: Geometry of the prism compressor. Please click here to view a larger version of this figure.
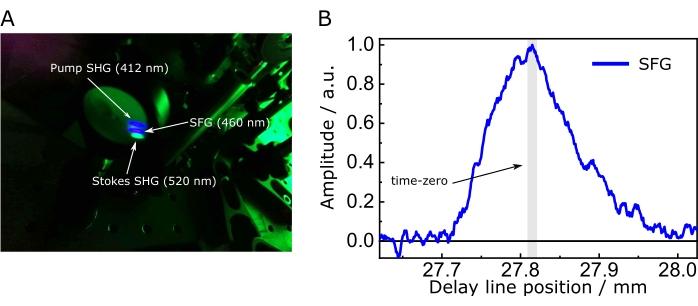
Figure 7: Sum-frequency generation to optimize spatiotemporal overlap. (A) SFG between the pump and Stokes and their respective SHG impinging on a screen. Here, a lens focused the pump and the Stokes beams onto the crystal, while a low-pass filter removed them. (B) Intensity of the SFG between pump and Stokes as a function of time delay. Set the time zero of the SRS setup at the position that maximizes the SFG. The asymmetry of the cross-correlation in B is due to the temporal profile caused by the etalon on the Stokes beam. Abbreviations: SFG = sum-frequency generation; SHG = second harmonic generation module; SRS = stimulated Raman scattering spectroscopy. Please click here to view a larger version of this figure.
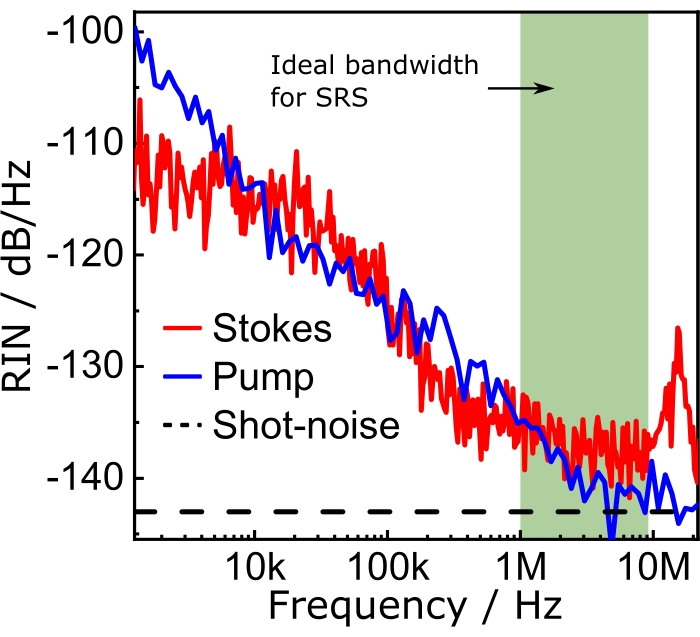
Figure 8: RIN spectra. The band highlighted in green shows the best spectral region for the SRS experiments. Modulating the Stokes beam at any frequency within this band guarantees that the effects of the laser noise on the SRS signal will be the lowest possible. Abbreviations: RIN = relative intensity noise; SRS = stimulated Raman scattering spectroscopy. Please click here to view a larger version of this figure.
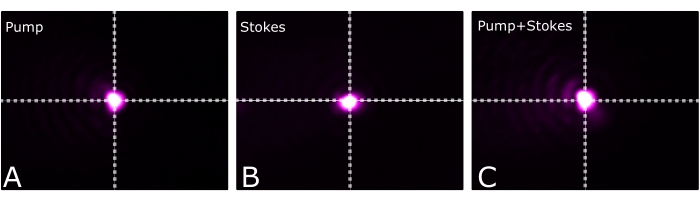
Figure 9: Beam profiles. (A) Pump, (B) Stokes, and (C) pump and Stokes. Please click here to view a larger version of this figure.
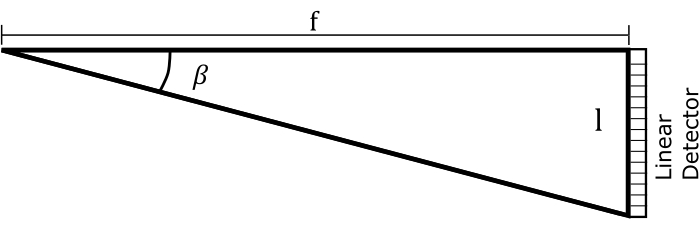
Figure 10: Assumed geometry for a dispersion grating and a photodiode array detector. Please click here to view a larger version of this figure.
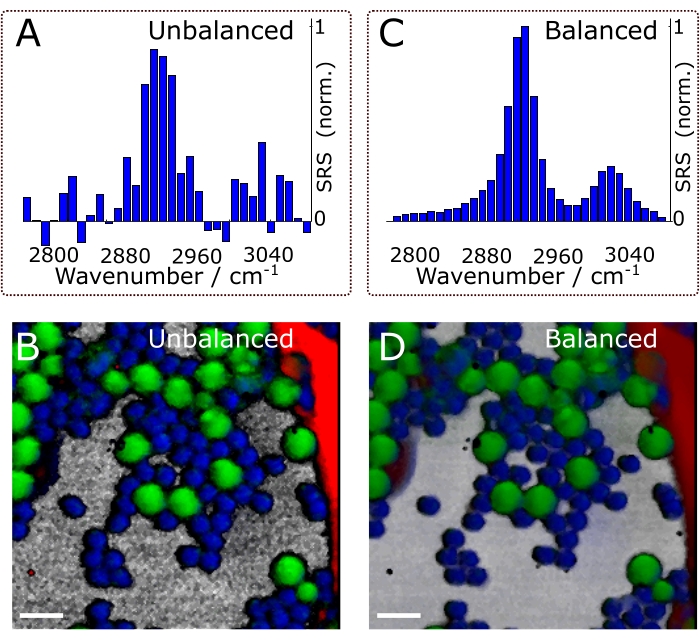
Figure 11. The effects of balanced detection. Effects on spectra (A, C) and chemical images (B, D). The composites shown in panels (B) and (D) are the final results of the experiments (i.e., after chemometric analysis of hyperspectral data. See protocol section 4 for details). Scale bars = 10 µm. Abbreviation: SRS = stimulated Raman scattering spectroscopy. Please click here to view a larger version of this figure.

Figure 12: A representative SRS hypercube acquired with broadband SRS microscopy. The x-y plane stores the coordinates of the scanned positions, while each vector along z registers an SRS spectrum. Abbreviation: SRS = stimulated Raman scattering spectroscopy. Please click here to view a larger version of this figure.
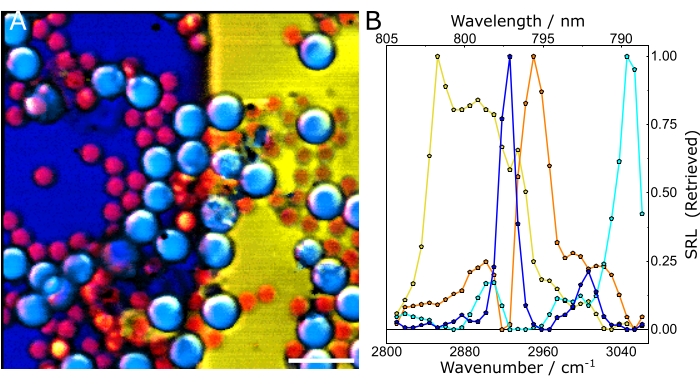
Figure 13: Chemometric analysis of hyperspectral SRS data. (A) Composite of the concentration maps of the different constituents of the sample. (B) Characteristic spectra of the chemical species. In both panels, yellow: olive oil, blue: DMSO, cyan: PS, and orange: PMMA. Scale bar = 20 µm (A). Abbreviations: SRS = stimulated Raman scattering spectroscopy; PS = polystyrene; PMMA = polymethyl methacrylate. Please click here to view a larger version of this figure.
Discussion
Broadband SRS microscopy is a powerful imaging technique that offers authentic chemical contrast to identify and disentangle the chemical constituents of a heterogeneous sample. The potential of this analytical tool can be beneficial to several research fields, ranging from materials science to histopathology. The downside of broadband SRS microscopy is the fact that it is technically demanding; the experimentalist not only requires know-how on broadband laser sources but also needs to manipulate the laser pulses to efficiently generate SRS, a signal that, in turn, needs to be measured with sophisticated detection schemes. This paper presents a protocol that describes a workflow to produce chemical maps of mixed chemical compounds using a multiplex broadband SRS microscope. Although the work described may be trivial for some laser physicists and nonlinear microscopists, it may not be the case for readers interested in the benefits of broadband SRS microscopy whose scientific knowledge resides outside these domains. Therefore, we aimed to detail every step to guide the wide audience interested in broadband SRS microscopy.
The protocol at hand started by showing how to prepare a simple yet spectroscopically rich sample composed of several strong and well-known Raman scatterers. We discussed how to obtain the broadband pump and narrowband Stokes beams necessary to set up an SRS microscope. Figure 5C shows a scheme of the SHG and OPO setups. Note that lens f1 focuses the fundamental beam onto LBO1 to generate the SHG, while a dichroic mirror reflects the SHG radiation and transmits the residual fundamental beam. A second lens f2 collimates the SHG beam. As f2 > f1, the SHG beam is expanded by a factor equal to f2/f1. A third lens f3 focuses the expanded SHG beam onto a second Type I LBO crystal (LBO2) cut at θ = 90° and φ = 29.0°. By pumping LBO2 with the aforementioned SGH (520 nm), radiation within the 680-910 nm range will emerge from LBO2 through difference-frequency generation (DFG), producing two beams: the signal and idler27 (Figure 5D,E). The latter is discarded while the former is amplified in the OPO cavity to deliver the pump pulses employed in the SRS experiments. The pump of the OPO at 520 nm, namely, the SHG beam, should not be confused with the pump of the SRS experiments (i.e., the signal beam of the OPO).
The contrast in SRS microscopy originates from a nonlinear signal generated at the focal spot of the microscope, a signal that demands confining a large number of photons in the sample plane at a given time. This photon confinement is achieved with a high numerical aperture (NA) microscope objective, an array of lenses that also sets the spatial resolution of the system: the higher the NA, the higher the spatial resolution. However, high NA objectives are densely packed with glass, which introduces positive GDD to pulsed radiation, a frequency chirp that ultimately broadens the temporal profile of the pulses39. Thus, the GDD introduced by the microscope objective might increase the duration of the broadband pump pulses, making it even longer than the Stokes temporal envelope and reducing the effective, accessible bandwidth of the Raman signal. Furthermore, this broadening might also introduce a distortion of the spectral profile of the measured SRS spectrum.
In CARS, the spectroscopically relevant signal emerges at wavelengths that differ from those of the excitation fields. A simple photomultiplier tube or charge-coupled device (CCD) camera can be used to integrate the CARS signal in time, summing up thousands of pulses to average out the laser noise. Instead, the SRS signal appears as a faint modulation transfer embedded within a strong and fluctuating laser background. Because this modulation is weak, the laser noise can readily overwhelm it, reducing both the imaging speed and the sensitivity of the SRS microscope. Therefore, before imaging, it is imperative to measure the relative intensity noise (RIN) to determine whether the laser is suitable for high-speed SRS imaging and to select the modulation frequency with the lowest noise. The RIN is defined as the noise power spectral density [δP(f), with W2/Hz units] of the laser normalized by the mean optical power (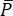 )40,41. In other words, the RIN describes the normalized laser fluctuations at different frequencies (Eq [4]).
)40,41. In other words, the RIN describes the normalized laser fluctuations at different frequencies (Eq [4]).
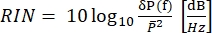 (4)
(4)
Thus, the RIN is a parameter of the SRS system that determines the ideal modulation frequency range for the experiments. For example, the olive bar in Figure 8 shows the ideal modulation frequency range for SRS imaging. In the case of narrowband SRS, the user should measure the RIN of both pump and Stokes to choose what beam needs to be modulated to achieve optimum performance. Note from Figure 8, for example, that the Stokes beam has a slightly higher RIN than the pump, implying that the SRG measurements would turn out noisier than their SRL counterparts. In the case of broadband SRS, the beam that should be modulated is the narrowband beam.
The angular dispersion D of the grating expresses the diffraction angle as a function of wavelength, and is defined as the derivative of the grating equation. For the Littrow configuration, the angular dispersion is given by Eq (5).
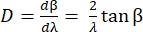 (5)
(5)
To get Eq (5), we assumed α = β, solved Eq (2) for m/d and inserted the result into dβ/ dλ. Note that in the Littrow configuration, β = sin-1(mλ/2d). Within the small-angle approximation, the change in position along the spectrum is fdβ ≈ dl (Figure 10). Thus, by inserting dβ into Eq (5), we can calculate the linear dispersion, a quantity with units of nm mm-1 using Eq (6):
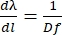 (6)
(6)
For a diffraction grating operating in the Littrow configuration with 1,851.85 grooves/mm, d = 540 nm. If we use the first-order diffraction of light at ~789 nm, D = 0.0027 rad nm-1. With an f = 750 mm lens, we get a linear dispersion of ≈ 0.5 nm mm-1, translating into ≈ 7.8 cm-1mm-1. Thus, the focal length of the lens determines the "density" of nm per mm at the detector plane: The longer the focal length, the fewer nm per mm obtained, increasing the space between the spectral lines of the broadband pump. Conversely, with shorter focal lengths, there will be more nm per mm at the detector plane, reducing the space occupied by the dispersed pump.
Balanced detection improves the image quality and sensitivity of noisy setups. For example, according to the RIN spectra shown in Figure 8 and considering typical SRS with an amplitude of 1 x 10-5, the unbalanced signal-to-noise ratio (SNR) is ≈60. Using balanced detection (i.e., close to the shot-noise), it is possible to attain an SNR of ≈145. Figure 11 shows spectra and composite images under balanced and unbalanced conditions. Naturally, the effects of balanced detection impact the final results of the experiments, namely, the chemical maps. Supported by these results, we emphasize that balanced detection is a powerful technique to counter the detrimental effects of laser fluctuations on image quality. It is worth mentioning that balanced detection is best suited for noisy lasers, such as fiber oscillators. SRS microscopes operating with quiet optical light sources (e.g., solid-state lasers), may not require balanced detection.
The protocol also explains an approach based on nonlinear optics to find the spatiotemporal overlap between the pulses of these beams. We described the advantages of using the 1st instead of the 0th diffraction-order of an AOM as the modulated Stokes beam. Further, the detrimental effects of dispersion on the SRS generation efficiency were described with suggestions of ways to mitigate them via a prism compressor. In addition, the protocol explains how to align the prisms and highlights three critical aspects to consider for optimum performance. We not only discuss the relevance of the RIN for SRS microscopy but also show how to measure it with a lock-in amplifier and, with the RIN spectrum, define the best modulation frequency. With a concrete example, this paper explains how the grating equation helps in designing the detection chain. Finally, the protocol illustrates, with real SRS data, the structure of the SRS hypercube and how to analyze it with a conventionally used scientific programming language.
This protocol has three minor limitations. First, the detection scheme employed in this contribution consists of a nonconventional, multichannel lock-in detector designed and built in-house by Sciortino et al.26 As demonstrated previously25, this detector can be replaced by an off-the-shelf balanced photodiode. Although this modification concerns only the detector and leaves the protocol virtually unchanged, with a single-photodiode, one needs to scan each spectral component on the detector instead of measuring them all at once. Second, this protocol employs inline balanced detection, which requires inserting several optical elements into the beam path. These optical elements increase the system complexity and lead to losses of optical power and pulse broadening.
Inline balanced detection also demands that the two pump replicas pass through the sample, a situation that may not be ideal for light-sensitive samples, such as living cells, or for strongly birefringent ones in which the two pump replicas may experience different optical properties, thus canceling the balanced detection. Third, the protocol relies on a home-built OPO, a device that may not be readily available. However, alternatives to the broadband spectra delivered by the OPO are the supercontinua from nonlinear optical fibers or bulk crystals. The latter could be employed only with low repetition rate lasers (up to 5 MHz). Thus, as with every experimental design, the protocol at hand has some limitations. However, they are minimal and do not compromise the success of this approach.
Although a reference sample is described here, this protocol can successfully disentangle chemical species within cells and animal and plant tissues, such as cellulose, lipidic species, or proteins, finding practical applications in different biochemical quests or as a diagnostics tool in histopathology. Similarly, this protocol can be a valuable tool in material sciences. For example, following this protocol, one can interrogate the molecular composition and concentration of polymeric species42. Furthermore, this methodology is compatible with other nonlinear microscopy techniques, such as broadband microscopy based on pump-probe43 and heterodyne CARS44, four-wave mixing processes that, as with SRS, also require two excitation light beams and modulation-transfer measurements. Finally, some of the information contained in this paper can be applied to nonlinear imaging techniques that do not rely on modulation transfer techniques, but require aligning two or more pulsed laser beams, such as conventional CARS45 and SFG microscopies46.
In summary, this protocol describes a powerful methodology based on broadband SRS microscopy to extract chemical maps and their characteristic SRS spectra from chemically heterogeneous mixtures, delivering datasets that allow straightforward quantitative data analysis. The versatility and simplicity of the method also give the interested reader the possibility to adapt it to different nonlinear techniques.
Acknowledgements
D. P. acknowledges funding from the European Union project CRIMSON under Grant Agreement No. 101016923 and the Regione Lombardia project NEWMED under Grant Agreement No. POR FESR 2014-2020. G. C. acknowledges funding from the European Union project GRAPHENE Core3 under grant agreement number 881603. G. C. also acknowledges funding from King Abdullah University of Science and Technology, Grant Award Number: OSR-2016-CRG5-3017-01.
Materials
| Name | Company | Catalog Number | Comments |
| Collection objective | Nikon | CFI Apo Lambda S 60x Oil, NA=1.4, Nikon | Oil immersion objective |
| Coverslips | Thermo Fisher | 043211-KJ | Quartz, cover slip for microscope slide, 25.4 x 25.4 x 0.15 mm |
| Delay line | Physik Instrumente (PI) | M-406.6PD | Precision microtranslation stage, 150 mm travel range |
| DMSO | Merck | D8418-500ML | Methylsulfinylmethane, Molecular Biology Grade DMSO, DMSO, Methyl Sulfoxide |
| Etalon | SLS Optics Ltd | Custom made | Anti reflective coating at 1,040 nm, Mounted in a 38 mm diameter x 35.5 mm long stainless steel cell with protective dust caps, and a 50 mm diameter ‘pinch-clamp’ mounting ring |
| Excitation objective | Nikon | CFI Plan Apo IR 60XC WI, NA=1.27, Nikon | Water immersion objective |
| Grating | LightSmyth | T-1850-800s Series | High Efficiency Transmission Grating T-1850-800s Series |
| Laser | Coherent | Custom made | Fidelity, HP |
| λ/2 | Thorlabs | SAHWP05M-1700 | Mounted superachromatic half-wave plate |
| PBS | Thorlabs | CM5-PBS203/M | 16 mm Cage-Cube-Mounted Polarizing Beamsplitter Cube, |
| PMMA beads | Merck | MFCD00198073 | Micro particles based on polymethacrylate |
| Prisms | Crisel | 320-8218 | LASER DISPERSING PRISMS in SF11 |
| PS beads | Merck | 72986-10ML-F | Micro particles based on polystyrene |
| YVO4 crystal | Dr. Sztatecsny GmbH | Custom made | thickness 8 mm, dia 1.00 cm, 1 689,00 689,00 suitable for 1" mount, coated for 850 - 1,100 nm |
References
- Stewart, S., Priore, R. J., Nelson, M. P., Treado, P. J. Raman Imaging. Annual Review of Analytical Chemistry. 5 (1), 337-360 (2012).
- Smekal, A. Zur quantentheorie der dispersion. Die Naturwissenschaften. 11 (43), 873-875 (1923).
- Raman, C. V., Krishnan, K. S. A new type of secondary radiation. Nature. 121 (3048), 501-502 (1928).
- Vanna, R., et al. Vibrational imaging for label-free cancer diagnosis and classification. La Rivista del Nuovo Cimento. 45, 107-187 (2021).
- Eckhardt, G., et al. Stimulated Raman scattering from organic liquids. Physical Review Letters. 9 (11), 455-457 (1962).
- Hellwarth, R. W. Theory of stimulated Raman scattering. Physical Review. 130 (5), 1850-1852 (1963).
- Maker, P. D., Terhune, R. W. Study of optical effects due to an induced polarization third order in the electric field strength. Physical Review. 137 (3), 801-818 (1965).
- Bloembergen, N. The stimulated Raman effect. American Journal of Physics. 35 (11), 989-1023 (1967).
- Levenson, M. D., Flytzanis, C., Bloembergen, N. Interference of resonant and nonresonant three-wave mixing in diamond. Physical Review B. 6 (10), 3962-3965 (1972).
- Polli, D., Kumar, V., Valensise, C. M., Marangoni, M., Cerullo, G. Broadband coherent Raman scattering microscopy. Laser & Photonics Reviews. 12 (9), 1800020 (2018).
- Rigneault, H., Berto, P. Tutorial: Coherent Raman light matter interaction processes. APL Photonics. 3 (9), 091101 (2018).
- Hu, F., Shi, L., Min, W. Biological imaging of chemical bonds by stimulated Raman scattering microscopy. Nature Methods. 16 (9), 830-842 (2019).
- Cheng, J. X., Xie, X. S. Vibrational spectroscopic imaging of living systems: An emerging platform for biology and medicine. Science. 350 (6264), (2015).
- Zumbusch, A., Holtom, G. R., Xie, X. S. Three-dimensional vibrational imaging by coherent anti-stokes raman scattering. Physical Review Letters. 82 (20), 4142-4145 (1999).
- Freudiger, C. W., et al. Label-free biomedical imaging with high sensitivity by stimulated Raman scattering microscopy. Science. 322 (5909), 1857-1861 (2008).
- Liu, Y., Lee, Y. J., Cicerone, M. T. Broadband CARS spectral phase retrieval using a time-domain Kramers-Kronig transform. Optics Letters. 34 (9), 1363 (2009).
- Valensise, C. M., et al. Removing non-resonant background from CARS spectra via deep learning. APL Photonics. 5 (6), 061305 (2020).
- Cheng, J. X., Xie, X. S. . Coherent Raman scattering microscopy. , (2012).
- Slipchenko, M. N., Oglesbee, R. A., Zhang, D., Wu, W., Cheng, J. X. Heterodyne detected nonlinear optical imaging in a lock-in free manner. Journal of Biophotonics. 5 (10), 801-807 (2012).
- Blume, R. J. Boxcar'' integrator with long holding times. Review of Scientific Instruments. 32 (9), 1016-1018 (1961).
- Saar, B. G., et al. Video-rate molecular imaging in vivo with stimulated Raman scattering. Science. 330 (6009), 1368-1370 (2010).
- Sarri, B., et al. Stimulated Raman histology: one to one comparison with standard hematoxylin and eosin staining. Biomedical Optics Express. 10 (10), 5378 (2019).
- Lu, F. K., et al. Label-free DNA imaging in vivo with stimulated Raman scattering microscopy. Proceedings of the National Academy of Sciences. 112 (37), 11624-11629 (2015).
- De la Cadena, A., et al. Broadband stimulated Raman imaging based on multi-channel lock-in detection for spectral histopathology. APL Photonics. 7 (7), (2022).
- Dela Cadena, A., Valensise, C. M., Marangoni, M., Cerullo, G., Polli, D. Broadband stimulated Raman scattering microscopy with wavelength-scanning detection. Journal of Raman Spectroscopy. 51 (10), 1951-1959 (2020).
- Sciortino, G., et al. Four-channel differential lock-in amplifiers with autobalancing network for stimulated Raman spectroscopy. IEEE Journal of Solid-State Circuits. 56 (6), 1859-1870 (2021).
- Coluccelli, N., et al. Tunable 30 fs light pulses at 1 W power level from a Yb-pumped optical parametric oscillator. Optics Letters. 42 (21), 4545 (2017).
- Monmayrant, A., Weber, S., Chatel, B. A newcomer's guide to ultrashort pulse shaping and characterization. Journal of Physics B: Atomic, Molecular and Optical Physics. 43 (10), 103001 (2010).
- Fork, R. L., Martinez, O. E., Gordon, J. P. Negative dispersion using pairs of prisms. Optics Letters. 9 (5), 150 (1984).
- Crisafi, F., et al. In-line balanced detection stimulated Raman scattering microscopy. Scientific Reports. 7 (1), 10475 (2017).
- Alem, M. Noise spectral density measured with lock-in amplifiers. Zurich Instruments Company Blog. , (2021).
- Palmer, C., Loewen, E. G. . Diffraction grating handbook. , (2005).
- . Multivariate curve resolution homepage Available from: https://mcrals.wordpress.com/download/mcr-als-2-0-toolbox/ (2021)
- Tauler, R. Multivariate curve resolution applied to second order data. Chemometrics and Intelligent Laboratory Systems. 30 (1), 133-146 (1995).
- de Juan, A., Jaumot, J., Tauler, R. Multivariate Curve Resolution (MCR). Solving the mixture analysis problem. Analytical Methods. 6 (14), 4964-4976 (2014).
- Zhang, D., et al. Quantitative vibrational imaging by hyperspectral stimulated Raman scattering microscopy and multivariate curve resolution analysis. Analytical Chemistry. 85 (1), 98-106 (2013).
- Chitra Ragupathy, I., Schweikhard, V., Zumbusch, A. Multivariate analysis of hyperspectral stimulated Raman scattering microscopy images. Journal of Raman Spectroscopy. 52 (9), 1630-1642 (2021).
- Brown, S. D., Tauler, R., Walczak, B. . Comprehensive Chemometrics: Chemical and Biochemical Data Analysis. , (2020).
- Guild, J. B., Xu, C., Webb, W. W. Measurement of group delay dispersion of high numerical aperture objective lenses using two-photon excited fluorescence. Applied Optics. 36 (1), 397 (1997).
- RP Photonics Encyclopedia. Article on "Relative Intensity Noise." Available from: https://www.rp-photonics.com/relative_intensity_noise.html (2021)
- Audier, X., Heuke, S., Volz, P., Rimke, I., Rigneault, H. Noise in stimulated Raman scattering measurement: From basics to practice. APL Photonics. 5 (1), 011101 (2020).
- Xu, S., Camp, C. H., Lee, Y. J. Coherent anti-Stokes Raman scattering microscopy for polymers. Journal of Polymer Science. , (2021).
- Davydova, D., de al Cadena, A., Akimov, D., Dietzek, B. Transient absorption microscopy: advances in chemical imaging of photoinduced dynamics. Laser & Photonics Reviews. 10 (1), 62-81 (2016).
- Potma, E. O., Evans, C. L., Xie, X. S. Heterodyne coherent anti-Stokes Raman scattering (CARS) imaging. Optics Letters. 31 (2), 241 (2006).
- Cheng, J. X., Volkmer, A., Xie, X. S. Theoretical and experimental characterization of coherent anti-Stokes Raman scattering microscopy. Journal of the Optical Society of America B. 19 (6), 1363 (2002).
- Raghunathan, V., Han, Y., Korth, O., Ge, N. H., Potma, E. O. Rapid vibrational imaging with sum frequency generation microscopy. Optics Letters. 36 (19), 3891 (2011).
This article has been published
Video Coming Soon
ABOUT JoVE
Copyright © 2025 MyJoVE Corporation. All rights reserved