The Evans Method
Source: Tamara M. Powers, Department of Chemistry, Texas A&M University
While most organic molecules are diamagnetic, wherein all their electrons are paired up in bonds, many transition metal complexes are paramagnetic, which has ground states with unpaired electrons. Recall Hund's rule, which states that for orbitals of similar energies, electrons will fill the orbitals to maximize the number of unpaired electrons before pairing up. Transition metals have partially populated d-orbitals whose energies are perturbed to varying extents by coordination of ligands to the metal. Thus, the d-orbitals are similar in energy to one another, but are not all degenerate. This allows for complexes to be diamagnetic, with all electrons paired up, or paramagnetic, with unpaired electrons.
Knowing the number of unpaired electrons in a metal complex can provide clues into the oxidation-state and geometry of the metal complex, as well as into the ligand field (crystal field) strength of the ligands. These properties greatly impact the spectroscopy and reactivity of transition metal complexes, and so are important to understand.
One way to count the number of unpaired electrons is to measure the magnetic susceptibility, χ, of the coordination compound. Magnetic susceptibility is the measure of magnetization of a material (or compound) when placed in an applied magnetic field. Paired electrons are slightly repelled by an applied magnetic field, and this repulsion increases linearly as the strength of the magnetic field increases. On the other hand, unpaired electrons are attracted (to a larger extent) to a magnetic field, and the attraction increases linearly with magnetic field strength. Therefore, any compound with unpaired electrons will be attracted to a magnetic field.1
When we measure the magnetic susceptibility, we obtain information on the number of unpaired electrons from the magnetic moment, µ. The magnetic susceptibility is related to the magnetic moment, µ by Equation 12:
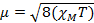 (1)
(1)
The constant 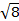 = [(3kB)/Nβ2)], where β= Bohr magneton of the electron (0.93 x 10-20 erg gauss-1), N = Avogadro's number, and kB = Boltzmann constant
= [(3kB)/Nβ2)], where β= Bohr magneton of the electron (0.93 x 10-20 erg gauss-1), N = Avogadro's number, and kB = Boltzmann constant
XM = molar magnetic susceptibility (cm3/mol)
T = temperature (K)
µ = magnetic moment, measured in units of Bohr magneton, µB = 9.27 x 10-24 JT-1
The magnetic moment for complexes is given by Equation 21:
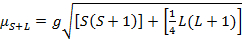 (2)
(2)
g = gyromagnetic ratio = 2.00023 µB
S = spin quantum number = ∑ms = [number of unpaired electrons, n]/2
L = orbital quantum number = ∑ml
This equation has both orbital and spin contributions. For first-row transition metal complexes, the orbital contribution is small and hence can be omitted, so the spin-only magnetic moment is given by Equation 3:
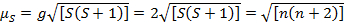 (3)
(3)
The spin-only magnetic moment can thus directly give the number of unpaired electrons. This approximation can also be made for heavier metals, though orbital contributions may be significant for second and third row transition metals. This contribution may be so significant that it inflates the magnetic moment enough that the compound appears to have more unpaired electrons than it does. Therefore, additional characterization may be required for these complexes.
In this experiment, the solution magnetic moment of tris(acetylacetonato)iron(III) (Fe(acac)3) is determined experimentally using Evans method in chloroform.
1. Preparation of Capillary Insert
- Using a lighter or other gas flame, melt the tip of a long Pasteur pipette. Gently rotate the pipette tip in the flame until a small bulb forms. Allow the glass to cool.
- In a scintillation vial, prepare a 50:1 (volume) solution of deuterated:proteo chloroform. Pipette 2 mL of deuterated solvent, and to this add 40 µL of proteo solvent. Cap the vial.
- Carefully add a few drops of the solvent mixture to the sealed glass pipette. Gently flick the tip of
Experimental Results
| Fe(acac)3 | Chloroform | |
| m (g) | 0.0051 | 0.874 |
| MW (g/mol) | 353.17 | n/a |
| n (mol) | 1.44⋅10-5 Application and Summary The Evans method is a simple and practical method for obtaining the magnetic susceptibility of soluble metal complexes. This provides the number of unpaired electrons in a metal complex, which is pertinent to the spectroscopy, magnetic properties, and reactivity of the complex. Measuring the magnetic susceptibility of paramagnetic species gives the number of unpaired electrons, which is a key property of metal complexes. As the reactivity of metal complexes is influenced by its electronic stru References
Tags Skip to... ABOUT JoVE Copyright © 2025 MyJoVE Corporation. All rights reserved |