Hooke's Law and Simple Harmonic Motion
Source: Ketron Mitchell-Wynne, PhD, Asantha Cooray, PhD, Department of Physics & Astronomy, School of Physical Sciences, University of California, Irvine, CA
Potential energy is an important concept in physics. Potential energy is the energy associated with forces that depend upon the position of an object relative to its surroundings. Gravitational potential energy, which is discussed in another video, is the energy associated that is directly proportional to the height of an object above the ground. Similarly, it is possible to define spring potential energy, which is directly proportional to the displacement of a spring from its relaxed state. A stretched or compressed spring has potential energy, as it has the ability to do work upon an object. The “ability to do work” is often quoted as the fundamental definition of energy.
This video will demonstrate the potential energy stored in springs. It will also verify the restoring force equation of springs, or Hooke’s Law. The spring constant is different for springs of different elasticities. Hooke’s law will be verified and the spring constant measured by attaching varying weights to a suspended spring and measuring the resulting displacements.
1. Measure the spring constant and potential energy of a spring and confirm the relationship between the mass and oscillatory period T.
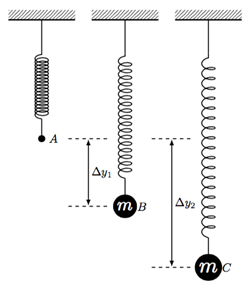
- Obtain a spring with a known spring constant, a stand to attach the spring to, at least 5 weights of varying masses that can be attached to the spring, a meter stick, and a stopwatch.
- Secure the stand to a solid foundation and attach the spring to the stand. Make sure that there is enough room below the spring for it to stretch without hitting the table or ground.
Representative results of the experiment, conducted with a spring of constant k = 10 N/m, are shown in Table 1. The plot of F versus the displacement Δy is plotted below in Figure 2. The linear function is fit with a line, and the slope of the line is equal to the spring constant, within a margin of error. The linearity of the result shows the validity of Hooke’s law (Equation 1).
Inspect <
The use of springs is ubiquitous in our everyday lives. The suspension of modern cars is made from springs that are properly damped. This requires knowledge of the spring constants. For smoother Cadillac rides, springs with a lower spring constant are used, and the ride is “mushier.” High-performance cars use springs with a higher spring constant for better handling. Diving boards are also made with springs of different spring constants, depending upon how much “bounce” is desired when diving off
Skip to...
Videos from this collection:

Now Playing
Hooke's Law and Simple Harmonic Motion
Physics I
61.2K Views

Newton's Laws of Motion
Physics I
75.5K Views

Force and Acceleration
Physics I
78.9K Views

Vectors in Multiple Directions
Physics I
182.2K Views

Kinematics and Projectile Motion
Physics I
72.4K Views

Newton's Law of Universal Gravitation
Physics I
190.4K Views

Conservation of Momentum
Physics I
43.2K Views

Friction
Physics I
52.8K Views

Equilibrium and Free-body Diagrams
Physics I
37.3K Views

Torque
Physics I
24.2K Views

Rotational Inertia
Physics I
43.4K Views

Angular Momentum
Physics I
35.8K Views

Energy and Work
Physics I
49.6K Views

Enthalpy
Physics I
59.8K Views

Entropy
Physics I
17.6K Views
Copyright © 2025 MyJoVE Corporation. All rights reserved