动力学分子理论定性地解释了各种气体定律所描述的行为。可以更定量地应用该理论的假设,以得出这些个体定律。 总体地,气体样品中的分子具有平均动能和平均速度;但它们各自以不同的速度运动。分子经常发生弹性碰撞,从而保持了动量。由于碰撞分子以不同的速度偏转,各个分子的速度变化很大。但是,由于涉及大量的分子和碰撞,因此分子速度分布和平均速度是恒定的。这种分子速度分布称为麦克斯韦-玻尔兹曼分布,它描述了具有给定速度的大量气体样品中分子的相对数目。
粒子的质量( m )和速度( u )的动能(KE)由下式给出:
以千克 (kg) 为单位表示质量,以米每秒 (m/s) 为单位表示速度将产生以焦耳为单位的能量值(J = kg·m 2 / s 2 )。为了处理大量的气体分子,我们使用速度和动能的平均值。在KMT中,粒子的均方根速度 u rms 被定义为 n的速度平方的均方根 =粒子数:
一摩尔粒子的平均动能KE avg 等于:
其中 M 是摩尔质量,单位为kg / mol。一摩尔气体分子的KE avg 也与气体的温度成正比,可以用以下等式描述:
其中 R 是气体常数,而 T 是开尔文温度。当在该方程式中使用时,气体常数的适当形式为8.314J / mol·K(8.314kg·m 2 / s 2 ·mol·K。可以将KE avg 的两个单独的方程组合并重新排列以产生分子速度和温度之间的关系:
如果气体的温度升高,则其KE avg 升高,更多的分子具有更高的速度,而更少的分子具有更低的速度,并且分布总体上朝着更高的速度移动,即向右移动。如果温度降低,则KE avg 降低,更多的分子具有较低的速度,较少的分子具有较高的速度,并且分布总体上朝着较低的速度移动,即向左移动。
在给定温度下,所有气体的分子均具有相同的KE avg 。气体的分子速度与分子质量直接相关。由较轻分子组成的气体具有更高的高速粒子和更高的 u rms ,其速度分布在相对较高的速度下达到峰值。由较重分子组成的气体具有较低的低速粒子,较低的 u rms ,以及在相对较低的速度达到峰值的速度分布。
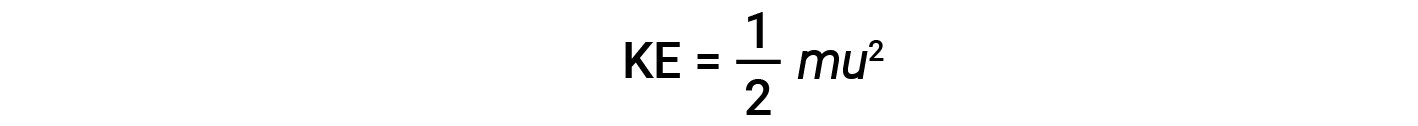
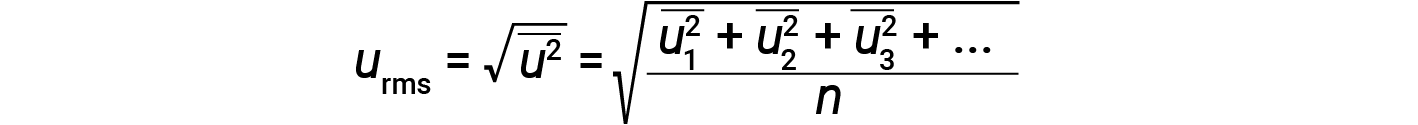
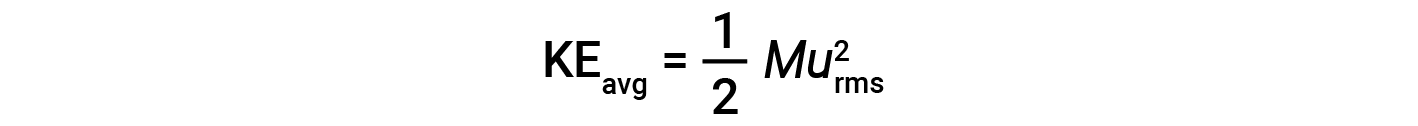
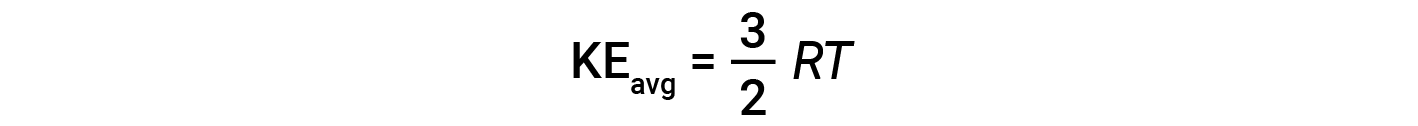
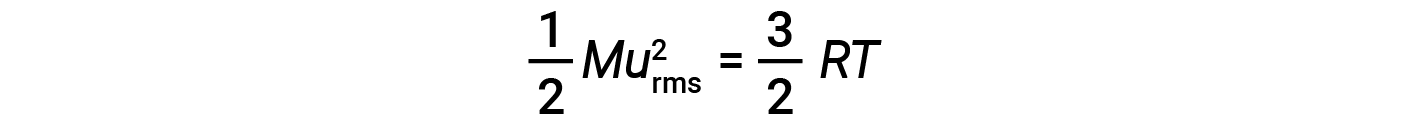
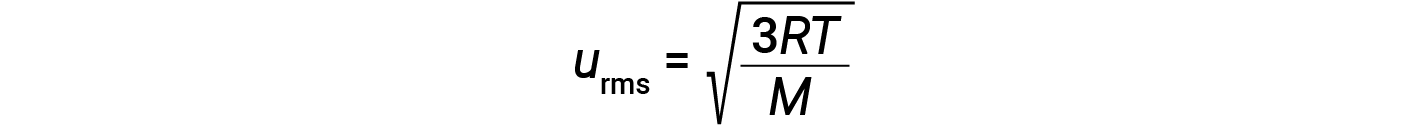
Tags
来自章节 5:

Now Playing
5.8 : 分子速度和动能
热化学
27.1K Views

5.1 : 压力和测量压力
热化学
35.5K Views

5.2 : 气体定律
热化学
65.3K Views

5.3 : 理想气体定律的应用:摩尔质量、密度和体积
热化学
56.0K Views

5.4 : 气体混合物-道尔顿分压定律
热化学
38.8K Views

5.5 : 化学计量学和气体
热化学
24.4K Views

5.6 : 动力学分子理论:基本假设
热化学
33.3K Views

5.7 : 动力学分子理论与气体定律
热化学
32.1K Views

5.9 : 渗出和扩散
热化学
28.4K Views

5.10 : 真实气体-偏离理想气体定律
热化学
34.2K Views
版权所属 © 2025 MyJoVE 公司版权所有,本公司不涉及任何医疗业务和医疗服务。