需要订阅 JoVE 才能查看此. 登录或开始免费试用。
Method Article
从层流到湍流条件下的规则基底表面初始粒子运动的可视化表征
摘要
提出了两种不同的方法来表征单个珠的初始粒子运动, 即从层流到湍流的沉积床几何函数。
摘要
本文提出了两种不同的实验方法来确定粒子运动的阈值, 作为从层流到紊流条件下的床的几何性质的函数。为此, 在规则基板上研究了单个珠的起动运动, 这些基体由均匀大小固定球体的单层组成, 它们定期排列在三角形和二次对称中。阈值以临界屏蔽数为特征。运动开始的判据被定义为从原来的平衡位置到相邻的位移。用成像系统识别位移和运动方式。层流是使用旋转流变仪与平行磁盘配置诱导。剪切雷诺数保持在1以下。采用开放射流试验剖面, 在低速风洞中诱导湍流流动。风机用变频器调节风速。速度剖面是用一个与热膜风速计连接的热导线探头来测量的。剪切雷诺数范围在40和150之间。利用罗塔所提出的对数速度定律和修正后的墙法, 从实验数据中推断出剪切速度。当移动珠部分暴露于所谓的水力过渡流体系中的湍流流动时, 后者是特别感兴趣的。剪切应力是在运动开始时估计的。结果表明, 在两种体制下, 静力角的影响很大, 而珠对剪切流的暴露也有代表性。
引言
初始粒子运动在广泛的工业和自然过程中遇到。环境例子包括河流和海洋中泥沙运输的初始过程、河床侵蚀或沙丘形成等其他1,2,3。气力输送4, 清除污染物或清洗表面5,6是典型的工业应用, 涉及粒子运动的开始。
由于广泛的应用, 粒子运动的开始已经被广泛研究了一个世纪, 主要是在湍流条件下7,8,9,10,11, 12,13,14,15。已有许多实验方法用于确定运动起始的阈值。研究内容包括粒子雷诺数13、16、17、18、19、20、相对流淹没等参数。21,22,23,24或几何因素作为静止的角度16,18,25, 暴露于流26,27,28,29,相对谷物凸起29或流向床斜率30。
包括湍流条件在内的阈值的当前数据大致分散12、31 , 结果通常看起来不一致24。这主要是由于在湍流条件下控制或确定流参数的固有复杂性13,14。此外, 泥沙运动的阈值强烈取决于运动模式,即滑动, 滚动或提升17和特征的初始运动31的标准。后者在侵蚀沉积床上可能不明确。
在过去十年中, 实验研究人员研究了层流流中的初始粒子运动32,33,34,35,36,37,38,39,40,41,42,43,44, 其中避免了与床交互的宽范围的长度刻度,45。在许多实际的情况下, 暗示沉淀, 粒子是相当小的, 粒子雷诺数保持低于约 546。另一方面, 层流可以产生像涟漪和沙丘一样的几何图案, 如湍流流做42,47。这两种方案中的班扬都反映了在基础物理47中的类比, 因此对粒子传输的重要洞察力可以从一个更好的受控实验系统48中获得。
在层流中, Charru et . 注意到, 均匀大小的珠子颗粒床的局部重排, 所谓的床装甲, 导致运动开始的门槛逐渐增加, 直到饱和条件达到32. 然而, 根据实验设置3644, 在不规则排列的沉积层中, 文献揭示了饱和条件的不同阈值。这种散射可能是由于对沉积物的定向、凸出层和致密性等粒子参数的控制困难所致。
本手稿的主要目的是详细描述如何将单个球体的起动作为水平沉积床几何性质的函数来刻画。为此, 我们使用常规几何, 由固定珠的单分子膜按照三角形或二次构型定期排列。类似于我们使用的常规衬底在微流控分析中的粒子模板组装 (49)、受限结构几何50或内部粒子诱导的 microdevices 的自组装等应用中发现。在微51中传输。更重要的是, 使用常规的衬底, 我们可以突出的影响, 地方几何和方向, 并避免任何 dubiety 的作用, 邻里。
在层流中, 我们观察到, 临界屏蔽数增加了 50%, 这取决于基体球体之间的间距, 从而使珠子暴露在流38上。类似地, 我们发现, 临界屏蔽号由两个因素所改变, 取决于基板的方向与流向38的方向。我们注意到, 不动的邻居只影响移动珠的开始, 如果他们比大约三粒径41。在实验结果的触发下, 我们最近提出了一个严格的分析模型, 可以预测爬行流限制40中的临界屏蔽数。该模型涵盖了从高暴露到隐藏珠的运动开始。
本手稿的第一部分论述了以往研究中所使用的剪切雷诺数的实验程序的描述, 再到1。层流是由旋转流变仪与平行配置引起的。在这个低雷诺数限制, 粒子不应该经历任何速度波动20和系统匹配所谓的水力平滑流, 其中粒子被淹没在粘性子层。
一旦形成层流的初始运动, 湍流的作用就会变得更加清晰。在这个想法的驱使下, 我们介绍了一个新的实验程序在第二部分的协议。采用开放射流试验段的哥廷根低速风洞, 可以在很大范围内确定临界屏蔽数, 包括水力过渡流和湍流体系。实验结果可以提供重要的洞察力和扭矩如何作用的粒子由于湍流流动取决于基体几何。此外, 这些结果可以作为一个基准, 为更复杂的模型在高 Re * 以类似的方式, 过去的工作在层流已经被用来养活半概率模型52或验证最近的数字模型53。我们提出一些典型的应用实例, 从40到150不等。
从初始平衡位置到下一粒子的运动, 建立了起始判据。图像处理用于确定运动开始的模式,即滚动、滑动、提升39、41。为此, 检测到手动标记的移动球体的旋转角度。该算法跟踪标记的位置, 并将其与球体的中心进行比较。在两个实验装置中进行了初步的实验, 阐明了临界屏蔽数与设置和相对流淹没的有限尺寸效应无关。实验方法的设计, 以排除任何其他参数依赖的关键盾号超越再 * 和几何性质的泥沙床。使用不同的流体-粒子组合来改变重复 *。临界屏蔽号的特征是埋葬程度的函数,, 由.  37作为
37作为 ,
, 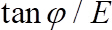 其中是养神的
其中是养神的 角度,即54的运动发生的临界角, 是曝光度, 定义为实际暴露于流中的横截面积的比值。移动珠的总横截面积。
角度,即54的运动发生的临界角, 是曝光度, 定义为实际暴露于流中的横截面积的比值。移动珠的总横截面积。
Access restricted. Please log in or start a trial to view this content.
研究方案
1. 初始粒子运动在爬行的流动极限。
注意: 测量是在旋转流变仪中进行的, 这是为这个特定的应用而修改的。
- 准备流变仪。
- 将空气供给与流变仪连接, 以避免损坏空气轴承。除空气过滤器外, 打开阀门, 直到系统中约5条的压力达到。
- 将流体循环器连接到测量板。确保珀尔半导体元件的软管连接到流变仪。打开流体循环器, 设定所需温度 (20 摄氏度)。
- 在流变仪上装载包含常规衬底的自定义容器。
- 将常规衬底从容器中取出, 用蒸馏水仔细清洗表面。用镜片清洗布干燥表面, 并去除可能的残余灰尘与鼓风机。
注: 常规基质为 15 x 15 毫米2的单分子膜, 由球形苏打-石灰玻璃珠 (405.9 µm 8.7) 制成。 - 使用0.4 毫米厚度双面胶带, 将常规衬底固定在容器中, 确保基板中心距车削轴的距离为21毫米。
- 将自定义适配器放在流变板上。
- 将自定义圆形容器装入板中, 确保平面前部面向侧面记录的成像系统。
注: 确保容器与水位完全水平 (0.6 毫米/米)。为此, 将水位放在与设备背面平行的容器上, 并将其与流变仪可调节的脚对其进行电平调整。重复这个过程, 把水位翻90度。
- 将常规衬底从容器中取出, 用蒸馏水仔细清洗表面。用镜片清洗布干燥表面, 并去除可能的残余灰尘与鼓风机。
- 打开流变仪。等待, 直到启动过程完成, 并且状态 "ok" 出现在设备屏幕上。
- 启动计算机和流变仪软件。初始化流变仪, 并将温度控制从软件的控制面板设置为所需值 (20 °c)。
- 安装定制的测量系统。设置与软件的零间隙。
注: 在设置零间隙之前, 请确保基板上没有移动珠子, 并且衬底边框不弯曲。在设置零隙时, 误差将导致在计算剪切速率时出现系统误差, 因此在临界屏蔽数的后续测量中。在计算临界屏蔽数时, 在间隙宽度中假定为0.05 毫米的绝对不确定度。 - 将测量板提起到30毫米, 然后将其卸下。
- 用大约70毫升 100 mPa·s 硅油填充容器。确保容器内流体的水平保持在2毫米以上。硅油不应覆盖透明板的上部。为热平衡等待大约15-20 分钟。在这段时间内, 调整成像系统 (参见协议中的步骤 2)。
注: 固定在这里的温度 (295.15 到 0.5) K, 是由连接到流变仪的一个珀尔元件控制的, 用外部温度计测量。实验中观察到小于 0.5 K 的波动。
- 调整成像系统。
- 开关 300 W 弧氙气灯。调整挠性导光导轨, 通过容器的透明壁照亮侧面的珠子。
- 调整 LED 光强, 避免衬底上的强光反射。
- 调整用于从顶部通过透明测量板记录粒子运动的成像系统。
- 从计算机启动映像软件, 然后从 "开始" 对话框中选择单色配置文件。
- 打开安装在容器顶部的成像系统的 768 x 576 CMOS 摄像机。启动现场视频。
- 调整水平定位阶段, 直到以前在基板中心标记的参照位置出现在图像的中心。
- 调整垂直定位阶段, 重点放在基板上。
- 小心地放置一个标记的苏打石灰玻璃球形 (405.9 @ 8.7) µm。
- 确保至少有一个标记放置在大约75% 的珠半径或大于旋转轴的距离上。如果不是这种情况, 请手动移动测量板以实现珠的运动到下一个平衡位置 (请参见图 2(a)作为参考)。
注意: 为确保在运动过程中的正确监视, 移动珠子标记有几个与45°隔开的斑点 (请参见图 3(a))。该代码包括一个简单的控制流语句, 以最小化标记 misassignment, 以计算旋转角度。有关详细信息, 请参阅 Agudo et 。201739。 - 打开用于设置照相机参数的对话框, 并将帧速率调整为 30 fps。调整曝光时间, 以确保标记与珠周长正确区分。
注: 在硅油中浸入 100 mPa·s 的苏打石灰玻璃球需要大约4秒的时间从最初的位置移动到分水岭到相邻的平衡位置。因此, 30 fps 的帧率允许不超过1% 的不确定性。
- 将测量板装入流变仪。
- 将测量距离设置为2毫米。
注: 顶部相机的焦点必须略有调整, 因为存在的有机玻璃板。 - 调整成像系统, 用于记录从侧面通过透明显微镜幻灯片的粒子运动。
- 打开安装在容器前面的成像系统的 4912 x 3684 CMOS 摄像机, 并启动现场视频。
- 调整平行于流变仪的垂直和水平定位阶段, 直到标记的珠子出现在图像的中心。
- 调整模块化变焦镜头, 直到视场包括基板的上表面、珠子和测量盘的底部。
- 调整垂直于流变仪上的水平定位工作台, 使其聚焦在珠子上。
- 打开用于设置照相机参数的对话框, 并将帧速率调整为 30 fps。
- 确定运动起始的临界转速。
- 使用流变仪软件将转速 ( n) 以每秒0.00025 转数的小增量从0.02 到0.05 的速度线性增加。
- 在 "测量" 窗口中, 双击该控件类型的单元格, 并编辑每秒0.02 到0.05 转的速度范围。
- 双击时间设置, 输入测量点的数量, 60, 每个测量的持续时间, 5 秒。
- 将表示旋转速度的表设置为时间函数。
- 从顶部和侧面摄像头打开现场视频。使用成像软件从两个摄像头开始录制视频序列。
- 使用流变仪软件开始测量。
注意: 建议在步骤1.3.1.1 之前进行一个较大步长的初步实验, 以便粗略估计初始运动发生的速度范围。例如, 在21毫米从转动的轴和使用 100 mPa·s 的硅油的距离, 玻璃珠移动在大约0.035 转每秒的自转速度。因此, 一个范围从0.02 到0.05 转每秒似乎适合的实验。 - 仔细看现场视频从顶部或从侧面相机和停止测量时, 珠从其平衡位置偏移。注意珠子穿过分界线环到相邻平衡位置的速度。所述旋转速度表示临界转速, nC。停止视频序列。
注: 确保步骤大小足够小, 使珠粒需要从其初始位置移动到相邻的时间间隔内的速度增加不涉及超过1% 的临界值。 - 把珠子放回原来的位置。这可以通过手动移动的旋转板, 直到珠取代一个位置回来。重复实验五次, 指出平均临界速度和标准偏差。
- 重复步骤1.3.1 到1.3.5 与一个不同的标记珠在2相邻的位置到基板的中心。
- 使用流变仪软件将转速 ( n) 以每秒0.00025 转数的小增量从0.02 到0.05 的速度线性增加。
- 分析数据。
- 确定运动模式: 根据 Agudo et 201739中所述的算法, 分析先前从顶部或侧面记录的图像序列。
- 确定临界屏蔽号和剪切雷诺数。
- 从以下等式中获取临界屏蔽号40
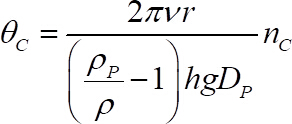 (1)
(1)
如果从步骤1.3.4 中获得了, 则是运动粘度, 和分别是粒子和液体密度, 是重力的加速度, 是移动珠直径, 所有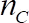



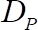 他们知道。是间隙宽度, 定义为从基底球体顶部到测量板的距离,
他们知道。是间隙宽度, 定义为从基底球体顶部到测量板的距离,  即2 毫米和r是粒子从车削轴的径向距离,即21 毫米。
即2 毫米和r是粒子从车削轴的径向距离,即21 毫米。 - 得到剪切雷诺数, 再根据剪切速度, 从以下等式:
 (2)
(2)
- 从以下等式中获取临界屏蔽号40
- 使用不同的常规基板重复1.1.3 到1.4.2 的过程。
- 使用不同的珠密度和不同的流体粘度, 以涵盖从蠕动的流动条件的广泛范围的1。
2. 在水力过渡和粗糙湍流的初期粒子运动。
注: 测量是在自定义的低速风洞中进行的, 它具有开放射流试验段、哥廷根型。
- 准备成像系统。
- 固定在测试部分中间的二次基板。
- 放置一个5毫米氧化铝珠以前标记在理想的初始位置 (110 毫米从领先的边缘和95毫米从侧面边缘)。
- 将高速照相机与宏透镜连接在一起, 并将其打开。调整宏透镜, 直到目标珠在图像中清晰。
- 在计算机上启动映像软件。激活 "实时摄像头", 并将 "采样率" 设置为 1000 fps。
- 开关 LED 光源和调整强度以及摄像机的焦距, 以达到清晰的粒子及其标记图像。
注意: 确保至少有一个标记放置在大约75% 的珠半径或大于旋转轴的距离 (请参见图 3(a)作为参考)。
- 确定运动开始时的临界风扇速度。
- 设置风扇速度井低于临界值 (大约 1400 rpm 为5毫米氧化铝珠)。
- 按成像软件上的触发器启动录制。
- 每十年代增加大约4到 6 rpm 的速度, 直到出现初始运动。
- 记下初始运动发生的临界速度值, 并停止视频序列。
- 在同一初始位置放置一个新的标记珠, 并重复该过程从2.2.1 到2.2.4 十次。注意每个测量的临界速度。
- 重复该过程从2.2.1 到2.2.5 在同一距离从领先的边缘, 但在65和125毫米从侧面边缘, 分别。注意每个测量的临界速度。
- 准备恒温热丝风速计 (CTA)。
- 将 CTA 控制功能设置为 "十年抵抗 00.00"。打开主电源, 等待大约15-20 分钟的预热。
- 插入短路探头, 并将 CTA 控制功能切换到电阻测量。调整零欧姆, 直到针放在红色标记中, 然后将控制功能切换回待机状态。
- 用微型热导线探头代替短路探头。将 CTA 控制功能切换到电阻测量。调整电阻开关, 直到针放在红色的标记。
注: 测量电阻对应于微型探头的耐寒性。测量值应与制造商提供的值一致 (3.32 Ω)。 - 切换 CTA 功能, 将电阻十年调整为5.5 Ω, 达到65% 左右的过热率。
- 用平均临界速度 (步进 2.2.4) 测量 CTA 的频率响应。
- 打开风扇并将风扇的转速设置为临界值, 约 1400 rpm。打开示波器。
- 切换 CTA 上的方波发生器。
- 在计算机上启动示波器软件, 并打开 CSV 模块以启用数据记录。选择通道 (CH1) 并保存记录数据, 即时间和电压, 在所需的文件名下。等待测量完成 (约3分钟)。
注意: 截止频率是从电压降至3db 级的响应时间计算的 (请参见图 4(a))。 - 将方形波形发生器关闭, 并将 CTA 功能设置为待机状态。
- 校准 CTA。
- 切换 CTA 功能进行操作。确保探头调整到足够高度, 使其位于自由流区。
- 将风扇转速设置为 200 rpm。用叶轮风速计测量自由流区的流向速度, 并读取示波器上的电压。
- 重复步骤2.4.2 为不同的转速与固定增量 50 rpm 高达约 1450 rpm (总共26读取)。
- 在 rpm 和测量的自由流流向速度之间建立相关性,.
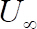 获取与从步骤2.2.5 到2.2.6 执行的每项测量的临界转速对应的临界速度.
获取与从步骤2.2.5 到2.2.6 执行的每项测量的临界转速对应的临界速度.  计算平均临界自由流速度、和测量的标准偏差.
计算平均临界自由流速度、和测量的标准偏差. 
- 根据三度多项式拟合建立速度与电压的相关性:
 (3)
(3)
在这里, 是在流向中测量的速度, 是以伏特 (V) 为单位测量的电压, 是拟合系数.

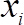 校准曲线显示在速度剖面测量前后的图 4(b)中。
校准曲线显示在速度剖面测量前后的图 4(b)中。
- 在临界条件下测量壁法线位置的流向速度。
- 从基板上取下标记的珠子。
- 调整水平定位级的手轮, 直到将热导线探头置于所需的初始位置 (从前缘的110毫米到95毫米的侧边)。
- 仔细调整垂直定位阶段的手轮, 直到探头尽可能靠近基体表面。通过相机看到耦合到宏观透镜, 以确保导线不接触承印物表面。在该位置的数字级指示器中设置零值。
警告:热导线是非常敏感的, 如果它触及的表面, 它会打破。为了安全起见, 我们将探头置于基底球体顶部的0.05 毫米的距离 (请参见图 1(e)作为参考)。这表示规范化的壁法线组件, 其中是起始测量值, 是剪切速度, 是工作温度下空气的运动粘度.
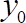
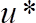
 请注意, 起始值低于, 其中黏度占主导地位的是
请注意, 起始值低于, 其中黏度占主导地位的是 55。
55。 - 将风扇转速设置为初始运动发生的平均转速, 请参阅步骤2.2.4。因此, 自由流速度对应于.

- 将采样率调整为 1 kSa, 在示波器上的样本数为 6000 (总采样时间为6秒)。选择通道 (CH1) 并开始测量。将录制数据保存在所需的文件名下。等待测量完成 (约3分钟)。
- 增加探针的壁法线位置由0.01 毫米增量0.4 毫米, 并且由0.1 毫米增量上升到10毫米的高度。这相当于速度剖面曲线的总137点。保存每个高度的记录数据。
- 分析数据。
- 计算各壁法线位置的平均流向速度和湍流强度。
- 运行自开发的算法来评估统计量。打开该脚本并选择包含校准曲线的文件夹和每个测量高度的存储数据。
注意: 脚本首先计算从校准曲线的拟合系数, 如 Eq 3 所示。对于每个高度, 它通过使用 Eq 3 计算瞬时流向速度, 通过自相关方法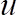 56计算积分时间刻度。此后, 它计算时间平均值、和根方速度 (), 这些样本被两次分隔为时间平均分析所需的积分时间.
56计算积分时间刻度。此后, 它计算时间平均值、和根方速度 (), 这些样本被两次分隔为时间平均分析所需的积分时间. 
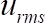
- 根据无量纲流向时间平均速度绘制无量纲垂直位置, 其中是基底球体的直径.
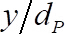
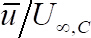
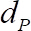 根据无量纲根平方速度绘制.
根据无量纲根平方速度绘制. 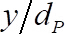
 图 4(c)-(d)描述了5毫米氧化铝珠的情况的结果。
图 4(c)-(d)描述了5毫米氧化铝珠的情况的结果。
- 运行自开发的算法来评估统计量。打开该脚本并选择包含校准曲线的文件夹和每个测量高度的存储数据。
- 从实验数据计算剪切速度。
- 将无量纲时间平均速度与对数速度分布匹配57
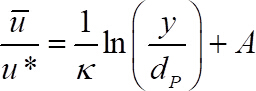 (5)
(5)
如果是剪切速度, 则是冯卡门的常量, 是依赖剪切雷诺 数26的常量.
数26的常量. 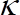
 图 4(c)中的实线是与时间平均速度相匹配的对数。
图 4(c)中的实线是与时间平均速度相匹配的对数。
注: 从拟合到实验数据, 可以看出剪切速度, 是通过以下步骤给出的:
 (6)
(6)
其中是对数拟合系数和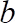
 20。
20。
粘性子层 () 在我们的实验中仍然位于基底球体的顶端. 在最严格的情况下, 应用罗塔20、58提供的修改速度定律替换 Eq 5。
在最严格的情况下, 应用罗塔20、58提供的修改速度定律替换 Eq 5。 (7)
(7)
其中和.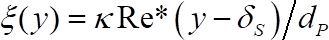
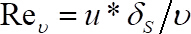 是粘性子层厚度, 可由
是粘性子层厚度, 可由
 55近似计算。
55近似计算。
该算法将实验数据拟合的剪切速度直接计算为 eq. 5 和 eq 7。图 4(c) 中的蓝色符号根据 Eq. 7 表示符合实验数据。
在70以上的情况下, 表示移动珠直径的 5%, 并使用从 eq. 5 或 eq 7 涉及在所采用的不确定性范围内的的变化.
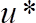 将图 4(c) 中的实线和蓝色符号比较为87.5。
将图 4(c) 中的实线和蓝色符号比较为87.5。
- 将无量纲时间平均速度与对数速度分布匹配57
- 确定运动模式: 根据 Agudo et 201739中所述的算法, 分析以前从侧面记录的图像序列。
- 确定临界屏蔽号和剪切雷诺数。
- 从以下等式中获取临界屏蔽号22
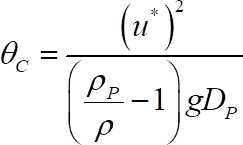 (8)
(8)
当从步骤10.2 中获取时, 和分别是粒子和流体密度, 是重力的加速度, 是移动珠直径, 所有这些都是已知的.


- 从以下方程中得到粒子雷诺数:
 (9)
(9) - 重复测量速度剖面的过程, 作为壁法线坐标系的函数, 步骤 2.5, 在同一个距离从前导边, 但在65和125毫米的宽度方向, 分别。
- 使用不同的珠粒大小和常规衬底, 重复2.1 到2.6.4.3 的过程。
- 从以下等式中获取临界屏蔽号22
- 计算各壁法线位置的平均流向速度和湍流强度。
Access restricted. Please log in or start a trial to view this content.
结果
图 1(a)表示用于描述爬行流限制中的临界护盾编号的实验设置示意图, 该协议1节。测量是在旋转流变仪中进行的, 为这个特定的应用进行了修改。一个直径为70毫米的透明有机玻璃板被仔细地固定在直径为25毫米的平行板上。测量系统的惯性因此在测量之前被调整了。一个定制的圆形容器, 直径为176毫米, 具有透明的墙壁, 与流变仪同心耦合...
Access restricted. Please log in or start a trial to view this content.
讨论
我们提出了两种不同的实验方法来表征初始粒子运动作为沉积床几何的功能。为此, 我们使用一个由三角形或二次对称排列的球体的单层, 这种方法使几何参数简化为单个几何。在蠕变流量极限中, 我们描述了用旋转浮子诱导层流剪切流的实验方法, 如前研究39,40,41。初步实验表明, 初始运动保持独立于基底的有限尺寸效应, 如径?...
Access restricted. Please log in or start a trial to view this content.
披露声明
作者没有什么可透露的
致谢
作者感谢未知的裁判为宝贵的意见, 并 Sukyung 崔, Byeongwoo 和 Baekkyoung 的合作, 建立实验。这项工作得到了21的大脑釜山项目在2017年。
Access restricted. Please log in or start a trial to view this content.
材料
| Name | Company | Catalog Number | Comments |
| MCR 302 Rotational Rheometer | Anton Paar | Induction of shear laminar flow | |
| Measuring Plate PP25 | Anton Paar | Induction of shear laminar flow | |
| Peltier System P-PTD 200 | Anton Paar | Keep temperature of silicon oils constant in the system at laminar flow | |
| Silicone oils with viscosities of approx. 10 and 100 mPas | Basildon Chemicals | Fluid used to induced the shear in the particles | |
| Soda-lime glass beads of (405.9 ± 8.7) μm | The Technical Glass Company | Construction of the regular substrates for laminar flow conditions | |
| Opto Zoom 70 Module 0.3x-2.2x | WEISS IMAGING AND SOLUTIONS GmbH | Imaging system for recording the bead motion in the rheometer | |
| 2 x TV-Tube 1.0x, D=35 mm, L=146.5 mm | WEISS IMAGING AND SOLUTIONS GmbH | Imaging system for recording the bead motion in the rheometer | |
| UI-1220SE CMOS Camera | IDS Imaging Development Systems GmbH | Imaging system for recording the bead motion in the rheometer | |
| UI-3590CP CMOS Camera | IDS Imaging Development Systems GmbH | Imaging system for recording the bead motion in the rheometer | |
| Volpi IntraLED 3 - LED light source | Volpi USA | Imaging system for recording the bead motion in the rheometer | |
| Active light guide diameter 5mm | Volpi USA | Imaging system for recording the bead motion in the rheometer | |
| 300 Watt Xenon Arc Lamp | Newport Corporation | Imaging system for recording the bead motion in the rheometer | |
| Wind-tunnel with open jet test section, Göttingen type | Tintschl BioEnergie und Strömungstechnik AG | Induction of turbulent flow | |
| Glass spheres of (2.00 ± 0.10) mm | Gloches South Korea | Construction of the regular substrates for turbulent flow conditions | |
| Alumina spheres of (5.00 ± 0.25) mm | Gloches South Korea | Targeted bead for experiments | |
| CTA Anemometer DISA 55M01 | Disa Elektronik A/S | Measurement of flow velocity in the wind tunnel | |
| Miniaure Wire Probe Type 55P15 | Dantec Dynamics | Measurement of flow velocity in the wind tunnel | |
| HMO2022 Digital Oscilloscope, 2 Analogue. Ch., 200MHz | Rohde & Schwarz | Measurement of flow velocity in the wind tunnel | |
| Phantom Miro eX1 High-speed Camera | Vision Research IncVis | Imaging system for recording the bead motion in the wind-tunnel | |
| Canon ef 180mm f/3.5 l usm macro lens | Canon | Imaging system for recording the bead motion in the wind-tunnel | |
| Table LED Lamp | Gloches South Korea | Imaging system for recording the bead motion in the wind-tunnel |
参考文献
- Groh, C., Wierschem, A., Aksel, N., Rehberg, I., Kruelle, C. A. Barchan dunes in two dimensions: Experimental tests for minimal models. Phys. Rev. E. 78, 021304(2008).
- Wierschem, A., Groh, C., Rehberg, I., Aksel, N., Kruelle, C. Ripple formation in weakly turbulent flow. Eur. Phys. J. E. 25, 213-221 (2008).
- Herrmann, H. Dune Formation in Traffic and Granular Flow. , Springer. Berlin. (2007).
- Stevanovic, V. D., et al. Analysis of transient ash pneumatic conveying over long distance and prediction of transport capacity. Powder Technol. 254, 281-290 (2014).
- Fan, F. -G., Soltani, M., Ahmadi, G., Hart, S. C. Flow-induced resuspension of rigid-link fibers from surfaces. Aerosol. Sci. Tech. 27, 97-115 (1997).
- Burdick, G., Berman, N., Beaudoin, S. Hydrodynamic particle removal from surfaces. Thin Solid Films. , 116-123 (2005).
- Chang, Y. Laboratory investigation of flume traction and transportation. Proceedings of the American Society of Civil Engineers. , 1701-1740 (1939).
- Paintal, A. A stochastic model of bed load transport. J. Hydraul. Res. 9, 527-554 (1971).
- Mantz, P. A. Incipient transport of fine grains and flakes by fluids-extended shield diagram. J. Hydr. Eng. Div.-Asce. 103, (1977).
- Yalin, M. S., Karahan, E. Inception of sediment transport. J. Hydr. Eng. Div.-Asce. 105, 1433(1979).
- Kuhnle, R. A. Incipient motion of sand-gravel sediment mixtures. J. Hydraul. Eng. 119, 1400-1415 (1993).
- Marsh, N. A., Western, A. W., Grayson, R. B. Comparison of methods for predicting incipient motion for sand beds. J. Hydraul. Eng. 130, 616-621 (2004).
- Vollmer, S., Kleinhans, M. G. Predicting incipient motion, including the effect of turbulent pressure fluctuations in the bed. Water Resour. Res. 43, (2007).
- Valyrakis, M., Diplas, P., Dancey, C. L., Greer, K., Celik, A. O. Role of instantaneous force magnitude and duration on particle entrainment. J. Geophys. Res.-Earth. 115, (2010).
- Dey, S., Ali, S. Z. Stochastic mechanics of loose boundary particle transport in turbulent flow. Phys. Fluids. 29, 055103(2017).
- Wiberg, P. L., Smith, J. D. Calculations of the critical shear stress for motion of uniform and heterogeneous sediments. Water Resour. Res. 23, 1471-1480 (1987).
- Ling, C. -H. Criteria for incipient motion of spherical sediment particles. J. Hydraul. Eng. 121, 472-478 (1995).
- Dey, S. Sediment threshold. Appl. Math. Model. 23, 399-417 (1999).
- Bravo, R., Ortiz, P., Pérez-Aparicio, J. Incipient sediment transport for non-cohesive landforms by the discrete element method (DEM). Appl. Math. Model. 38, 1326-1337 (2014).
- Ali, S. Z., Dey, S. Hydrodynamics of sediment threshold. Phys. Fluids. 28, 075103(2016).
- Yalin, M. S. Mechanics of sediment transport. , Pergamon Press. California. (1977).
- Graf, W. H., Sueska, L. Sediment transport in steep channels. Journal of Hydroscience and Hydraulic Engineering. 5, 233-255 (1987).
- Recking, A. An experimental study of grain sorting effects on bedload. , Lyon. Doctor in Sciences thesis, Institut National des Sciences Appliques de Lyon (2006).
- Roušar, L., Zachoval, Z., Julien, P. Incipient motion of coarse uniform gravel. J. Hydraul. Res. 54, 615-630 (2016).
- Miller, R. L., Byrne, R. J. The angle of repose for a single grain on a fixed rough bed. Sedimentology. 6, 303-314 (1966).
- Fenton, J., Abbott, J. Initial movement of grains on a stream bed: the effect of relative protrusion. Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences. 352, 523-537 (1977).
- Kirchner, J. W., Dietrich, W. E., Iseya, F., Ikeda, H. The variability of critical shear stress, friction angle, and grain protrusion in water-worked sediments. Sedimentology. 37, 647-672 (1990).
- Armanini, A., Gregoretti, C. Incipient sediment motion at high slopes in uniform flow condition. Water Resour. Res. 41, (2005).
- Chin, C., Chiew, Y. Effect of bed surface structure on spherical particle stability. J. Waterw. Port Coast. 119, 231-242 (1993).
- Whitehouse, R., Hardisty, J. Experimental assessment of two theories for the effect of bedslope on the threshold of bedload transport. Mar. Geol. 79, 135-139 (1988).
- Buffington, J. M., Montgomery, D. R. A systematic analysis of eight decades of incipient motion studies, with special reference to gravel-bedded rivers. Water Resour. Res. 33, 1993-2029 (1997).
- Charru, F., Mouilleron, H., Eiff, O. Erosion and deposition of particles on a bed sheared by a viscous flow. J. Fluid Mech. 519, 55-80 (2004).
- Loiseleux, T., Gondret, P., Rabaud, M., Doppler, D. Onset of erosion and avalanche for an inclined granular bed sheared by a continuous laminar flow. Phys. Fluids. 17, 103304(2005).
- Charru, F., Larrieu, E., Dupont, J. -B., Zenit, R. Motion of a particle near a rough wall in a viscous shear flow. J. Fluid Mech. 570, 431-453 (2007).
- Ouriemi, M., Aussillous, P., Medale, M., Peysson, Y., Guazzelli, É Determination of the critical Shields number for particle erosion in laminar flow. Phys. Fluids. 19, 061706(2007).
- Lobkovsky, A. E., Orpe, A. V., Molloy, R., Kudrolli, A., Rothman, D. H. Erosion of a granular bed driven by laminar fluid flow. J. Fluid Mech. 605, 47-58 (2008).
- Martino, R., Paterson, A., Piva, M. Onset of motion of a partly hidden cylinder in a laminar shear flow. Phys. Rev. E. 79, 036315(2009).
- Agudo, J., Wierschem, A. Incipient motion of a single particle on regular substrates in laminar shear flow. Phys. Fluids. 24, 093302(2012).
- Agudo, J., et al. Detection of particle motion using image processing with particular emphasis on rolling motion. Rev. Sci. Instrum. 88, 051805(2017).
- Agudo, J., et al. Shear-induced incipient motion of a single sphere on uniform substrates at low particle Reynolds numbers. J. Fluid Mech. 825, 284-314 (2017).
- Agudo, J., Dasilva, S., Wierschem, A. How do neighbors affect incipient particle motion in laminar shear flow? Phys. Fluids. 26, 053303(2014).
- Seizilles, G., Lajeunesse, E., Devauchelle, O., Bak, M. Cross-stream diffusion in bedload transport. Phys. Fluids. 26, 013302(2014).
- Seizilles, G., Devauchelle, O., Lajeunesse, E., Métivier, F. Width of laminar laboratory rivers. Phys. Rev. E. 87, 052204(2013).
- Hong, A., Tao, M., Kudrolli, A. Onset of erosion of a granular bed in a channel driven by fluid flow. Phys. Fluids. 27, 013301(2015).
- Derksen, J., Larsen, R. Drag and lift forces on random assemblies of wall-attached spheres in low-Reynolds-number shear flow. J. Fluid Mech. 673, 548-573 (2011).
- Happel, J., Brenner, H. Low Reynolds Number Hydrodynamics: With Special Applications to Particulate Media. , Martinuis Nijhoff. The Hague. (1983).
- Lajeunesse, E., et al. Fluvial and submarine morphodynamics of laminar and near-laminar flows: A synthesis. Sedimentology. 57, 1-26 (2010).
- Aussillous, P., Chauchat, J., Pailha, M., Médale, M., Guazzelli, É Investigation of the mobile granular layer in bedload transport by laminar shearing flows. J. Fluid Mech. 736, 594-615 (2013).
- Thompson, J. A., Bau, H. H. Microfluidic, bead-based assay: Theory and experiments. J. Chromatogr. B. 878, 228-236 (2010).
- Sawetzki, T., Rahmouni, S., Bechinger, C., Marr, D. W. In situ assembly of linked geometrically coupled microdevices. Proceedings of the National Academy of Sciences. 105, 20141-20145 (2008).
- Amini, H., Sollier, E., Weaver, W. M., Di Carlo, D. Intrinsic particle-induced lateral transport in microchannels. Proceedings of the National Academy of Sciences. 109, 11593-11598 (2012).
- Soepyan, F. B., et al. Threshold velocity to initiate particle motion in horizontal and near-horizontal conduits. Powder Technol. 292, 272-289 (2016).
- Deskos, G., Diplas, P. Incipient motion of a non-cohesive particle under Stokes flow conditions. International Journal of Multiphase Flow. , (2017).
- Julien, P. Y. Erosion and sedimentation. , Cambridge University Press. Cambridge. (2010).
- Jimenez, J. Turbulent flows over rough walls. Annu. Rev. Fluid Mech. 36, 173-196 (2004).
- O’neill, P., Nicolaides, D., Honnery, D., Soria, J. 15th Australasian Fluid Mechanics Conference. , The University of Sydney. 1-4 (2006).
- Schlichting, H. Boundary-Layer Theory. , McGraw-Hill. New York. (1979).
- Rotta, J. Das in wandnähe gültige Geschwindigkeitsgesetz turbulenter Strömungen. Arch. Appl. Mech. 18, 277-280 (1950).
- Schlichting, H., Gersten, K., Krause, E., Oertel, H. Boundary-layer theory. 7, Springer. (1955).
- Bruun, H. H. Hot-wire anemometry-principles and signal analysis. , Oxford: University Express. Oxford. (1995).
- Fan, D., Cheng, X., Wong, C. W., Li, J. -D. Optimization and Determination of the Frequency Response of Constant-Temperature Hot-Wire Anemometers. AIAA J. , 1-7 (2017).
- Valyrakis, M., Diplas, P., Dancey, C. L. Entrainment of coarse particles in turbulent flows: An energy approach. J. Geophys. Res.-Earth. 118, 42-53 (2013).
- Valyrakis, M., Diplas, P., Dancey, C. L. Entrainment of coarse grains in turbulent flows: An extreme value theory approach. Water Resour. Res. 47, (2011).
- Dey, S., Das, R., Gaudio, R., Bose, S. Turbulence in mobile-bed streams. Acta Geophys. 60, 1547-1588 (2012).
- Wu, F. -C., Chou, Y. -J. Rolling and lifting probabilities for sediment entrainment. J. Hydraul. Res. 129, 110-119 (2003).
- Leighton, D., Acrivos, A. The lift on a small sphere touching a plane in the presence of a simple shear flow. Z. Angew. Math. Phys. 36, 174-178 (1985).
- Tuyen, N. B., Cheng, N. -S. A single-camera technique for simultaneous measurement of large solid particles transported in rapid shallow channel flows. Exp. Fluids. 53, 1269-1287 (2012).
- Gollin, D., Bowman, E., Shepley, P. Methods for the physical measurement of collisional particle flows. IOP Conference Series: Earth and Environmental Science. 26, 012017(2015).
- Amon, A., et al. Focus on Imaging Methods in Granular Physics. Rev. Sci. Instrum. 88, (2017).
- Mouilleron, H., Charru, F., Eiff, O. Inside the moving layer of a sheared granular bed. J. Fluid Mech. 628, 229-239 (2009).
- Diplas, P., et al. The role of impulse on the initiation of particle movement under turbulent flow conditions. Science. 322, 717-720 (2008).
- Coleman, N. L. A theoretical and experimental study of drag and lift forces acting on a sphere resting on a hypothetical streambed. International Association for Hydraulic Research, 12th Congress, proceedings. 3, 185-192 (1967).
- El-Gabry, L. A., Thurman, D. R., Poinsatte, P. E. Procedure for determining turbulence length scales using hotwire anemometry. , NASA Technical Reports NASA/TM-2014-218403 (2014).
- Roach, P. The generation of nearly isotropic turbulence by means of grids. Int. J. Heat Fluid Fl. 8, 82-92 (1987).
Access restricted. Please log in or start a trial to view this content.
转载和许可
请求许可使用此 JoVE 文章的文本或图形
请求许可探索更多文章
This article has been published
Video Coming Soon
版权所属 © 2025 MyJoVE 公司版权所有,本公司不涉及任何医疗业务和医疗服务。