29.4 : Magnetic Field Due To A Thin Straight Wire
Consider an infinitely long straight wire carrying a current I. The magnetic field at point P at a distance a from the origin can be calculated using the Biot-Savart law.
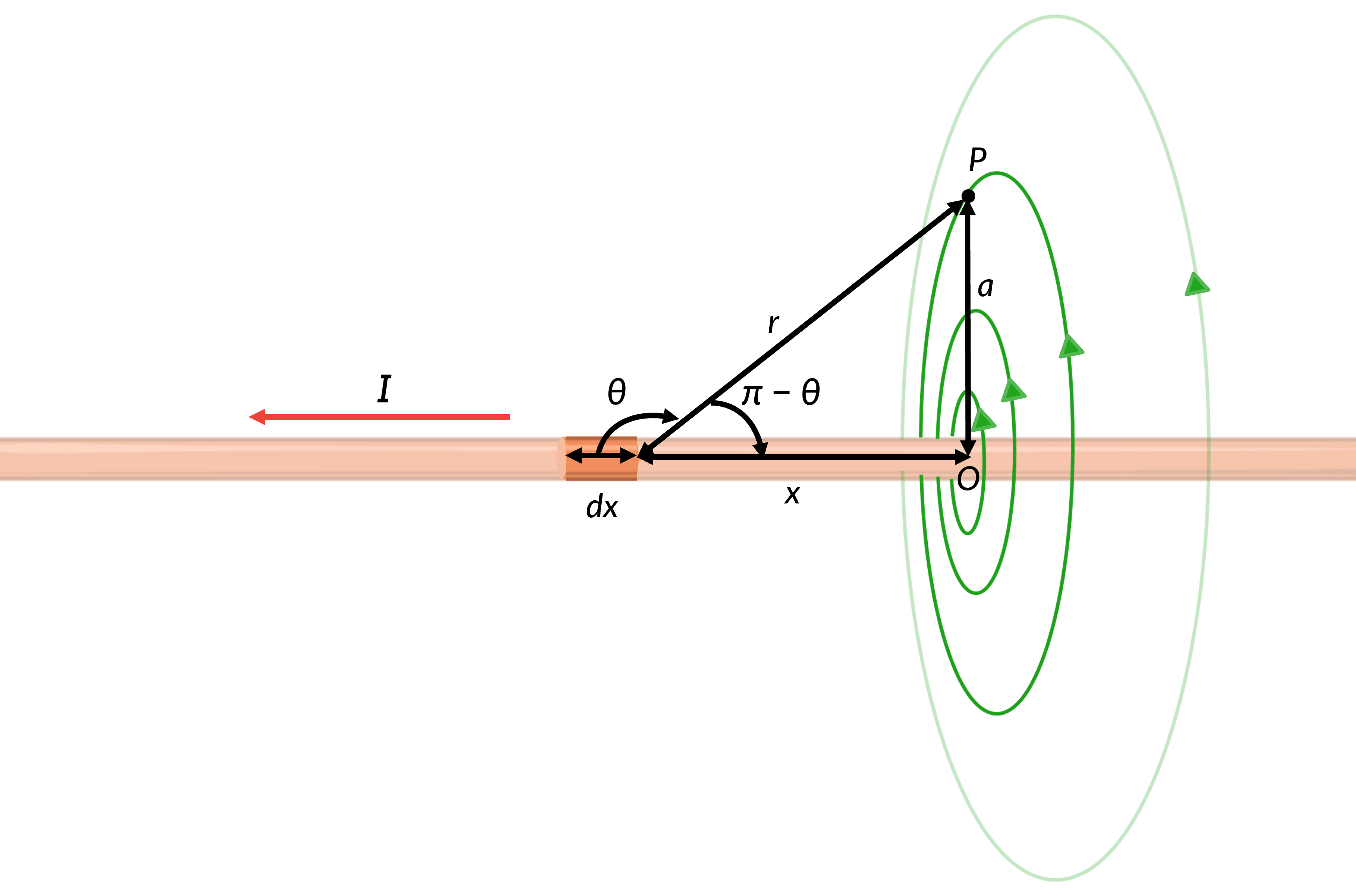
Consider a current element dx at a distance x from the origin. The current element makes an angle ÃÂø with the line joining dx and P. Using the Pythagorus theorum to express the distance between the current element and the point, the magnetic field due to the current element at point P can be estimated using Equation 1.
The wire is symmetrical about the origin. Hence, integrating Equation 1 within the limits of zero to infinity gives the equation for the magnetic field in terms of the current and the distance of point P from the wire.
The magnetic field lines of the infinite wire are circular and centered at the wire, and they are identical at every plane perpendicular to the wire. Since the intensity of the field decreases with the distance from the wire, the spacing of the field lines also increases correspondingly with distance.
The right-hand rule gives the direction of magnetic field lines. If the thumb points along the current, the fingers wrap around the wire in the same way as the magnetic field. Therefore, the field points into the page at point P. The magnetic fields due to all the current elements have the same direction.
Aus Kapitel 29:

Now Playing
29.4 : Magnetic Field Due To A Thin Straight Wire
Sources of Magnetic Fields
4.7K Ansichten

29.1 : Magnetfeld durch bewegte Ladungen
Sources of Magnetic Fields
8.3K Ansichten

29.2 : Biot-Savart-Gesetz
Sources of Magnetic Fields
5.8K Ansichten

29.3 : Biot-Savart-Gesetz: Problemlösung
Sources of Magnetic Fields
2.4K Ansichten

29.5 : Magnetfeld durch zwei gerade Drähte
Sources of Magnetic Fields
2.3K Ansichten

29.6 : Magnetische Kraft zwischen zwei parallelen Strömen
Sources of Magnetic Fields
3.4K Ansichten

29.7 : Magnetfeld einer Stromschleife
Sources of Magnetic Fields
4.3K Ansichten

29.8 : Divergenz und Krümmung des Magnetfeldes
Sources of Magnetic Fields
2.7K Ansichten

29.9 : Das Amperesche Gesetz
Sources of Magnetic Fields
3.6K Ansichten

29.10 : Amperes Gesetz: Problemlösung
Sources of Magnetic Fields
3.5K Ansichten

29.11 : Magnetspulen
Sources of Magnetic Fields
2.4K Ansichten

29.12 : Magnetfeld eines Magneten
Sources of Magnetic Fields
3.7K Ansichten

29.13 : Ringkerne
Sources of Magnetic Fields
2.8K Ansichten

29.14 : Magnetisches Vektorpotential
Sources of Magnetic Fields
522 Ansichten

29.15 : Potential durch ein magnetisiertes Objekt
Sources of Magnetic Fields
252 Ansichten
See More
Copyright © 2025 MyJoVE Corporation. Alle Rechte vorbehalten