Zum Anzeigen dieser Inhalte ist ein JoVE-Abonnement erforderlich. Melden Sie sich an oder starten Sie Ihre kostenlose Testversion.
Method Article
Gestaltung der Amplitude und Phase von Laserstrahlen durch den Einsatz einer Phase nur räumlichen Lichtmodulator
In diesem Artikel
Zusammenfassung
Wir zeigen, wie Sie den komplexen Bereich der Laserstrahlen zu kodieren, durch Verwendung eines Einphasen-Elements. Ein gemeinsamer Weg-Interferometer wird eingesetzt, um die Phaseninformation angezeigt in einer Phase nur räumlichen Lichtmodulator schließlich das gewünschte komplexes Feld Muster am Ausgang eines optischen imaging Systems abrufen zu mischen.
Zusammenfassung
Dieser Artikel soll die Nutzung einer interferometrischen Methode für die Codierung von komplexen Felder zugeordnet kohärente Laserstrahlung visuell demonstrieren. Die Methode basiert auf der kohärenten Summe zwei gleichmäßige Wellen, zuvor durch räumliche Multiplexen ihre Phasen in einer Phase nur räumlichen Lichtmodulator (SLM) kodiert. Hier die Interferenz-Prozess erfolgt durch räumliche Filterung der Lichtfrequenzen auf der Fourier-Ebene von bestimmten imaging-System. Die korrekte Umsetzung dieser Methode kann beliebige Phase und Amplitude Informationen am Ausgang des optischen Systems abgerufen werden.
Es ist eine auf der Achse, anstatt einfallenden Codierung Technik, mit einem direkten Weiterverarbeitung-Algorithmus (keine iterative Schleife), und frei von kohärenten Lärm (Fleck). Das komplexe Feld kann am Ausgang des optischen Systems, mit Ausnahme von gewissen Verlust an Auflösung durch die Frequenz Filterprozess genau abgerufen werden. Die wichtigste Einschränkung der Methode stammen möglicherweise aus der Unfähigkeit bei Vielfachheiten höher als die Refresh-Rate von der SLM betreiben. Anwendungen beinhalten, aber beschränken sich nicht auf lineare und nichtlineare Mikroskopie, Strahl Formen oder Laser Mikrobearbeitung von Materialoberflächen.
Einleitung
Fast alle Laser-Anwendungen sind in einem engen Zusammenhang mit dem Management der optischen Wellenfront des Lichts. Bei der achsnahen Angleichung kann das komplexe Feld zugeordnete Laserstrahlung durch zwei Begriffe, die Amplitude und der Phase beschrieben werden. Nachdem die Kontrolle über diese beiden Begriffe ist notwendig, um die zeitliche und die räumliche Struktur von Laserstrahlen auf ändern wird. Im Allgemeinen können die Amplitude und der Phase eines Laserstrahls richtig durch verschiedene Methoden, einschließlich der Verwendung von optischen Komponenten dieses Bereichs von einzelnen Masse Objektive, Strahlteiler und Spiegel auf komplexe Geräte wie verformbaren Spiegel oder räumliche Licht geändert werden Modulatoren. Hier zeigen wir eine Methode zum Codieren und Rekonstruktion von komplexen Bereich der kohärenten Laserstrahlen basiert auf Dual-Phase-Hologramm Theorie1und die Nutzung einer gemeinsamen-Pfad-Interferometers.
Heutzutage gibt es eine Vielzahl von Methoden, um den komplexen Bereichen Laser Strahlen2,3,4,5kodieren. In diesem Zusammenhang setzen einige bewährten Methoden, Phase und Amplitude Modulation zu produzieren auf die Verwendung von digitalen Hologrammen6. Eine Gemeinsamkeit bei allen diesen Methoden ist die Notwendigkeit zur Erzeugung eines räumlichen Versatz die nullte Ordnung aus der Reflexion des Lichtes auf das SLM-Display die gewünschte Ausgabe-Balken getrennt. Diese Methoden sind grundsätzlich außerhalb der Hauptachse (in der Regel anwenden für die erste Beugungsordnung das Gitter), Einsatz von Phase Gitter nicht nur die Phase zu kodieren, sondern auch notwendige Amplitudenmodulation einzuführen. Amplitudenmodulation erfolgt insbesondere durch räumlich Senkung der Gitter-Höhe, die die Beugungseffizienz deutlich verschlechtert. Der Hologramm Wiederaufbauprozess wird meist eine ungefähre, aber nicht genaue, Rekonstruktion der Amplitude und Phase der gewünschten komplexen Feldes. Diskrepanzen zwischen Theorie und Experiment scheinen aus eine falsche Codierung die Amplitude Informationen sowie andere experimentelle Probleme während die räumliche Filterung der ersten Beugungsordnung oder durch SLM Pixilation Effekte. Darüber hinaus kann die Intensität Profil des Eingangs Strahls Beschränkungen auf die Ausgangsleistung einführen.
Im Gegensatz dazu mit dem eingeführten Methode7, alle Licht-Management auf der Achse erfolgt sehr praktisch, aus Sicht der experimentellen. Darüber hinaus nutzt es in Betracht ziehen, in der achsnahen Annäherung, das komplexe Feld zugeordnete Laserstrahlen als Summe der zwei gleichmäßige Wellen. Die Amplitude Information ist dazu durch die Interferenz dieser gleichmäßige Wellen. In der Praxis solche Störungen erfolgt durch räumliche Filterung der Lichtfrequenzen auf der Fourier-Ebene eines bestimmten imaging Systems. Zuvor sind die Phase Muster verbunden mit den gleichmäßigen Wellen räumlich gemultiplext und in einer Phase nur SLM (platziert auf der Ebene der Eingang dieses imaging Systems) codiert. Daher kann die ganze optische Einrichtung als einen gemeinsamen Weg Interferometer (sehr robust gegenüber mechanischen Erschütterungen, Temperaturschwankungen oder optische Verzerrungen) angesehen werden. Bitte beachten Sie, dass die oben genannten Störungen Prozess Alternativ erreicht werden kann, mit anderen optischen Layouts: mit ein paar Phase nur SLMs richtig platziert innerhalb einer typischen Zweiarm-Interferometer oder durch Zeit nacheinander Codierung der zwei-Phasen- Muster in der SLM (frühere Einführung eines Referenz-Spiegels in der optische Aufbau). In beiden Fällen gibt es keine Notwendigkeit der räumlichen Filterung und folglich ohne Verlust der räumlichen Auflösung, auf Kosten der Erhöhung der Komplexität des optischen Systems sowie der Alignment-Prozess. Hier sollte auch betont werden, dass durch die Verwendung dieser Codierungsmethode, das gesamte Spektrum der gewünschten komplexen Feldes genau abgerufen , bei der Fourier-Ebene sein kann nach dem filtern alle Beugung Bestellungen aber die nullte einer.
Auf der anderen Seite die Effizienz der Methode hängt von mehreren Faktoren ab: den Angaben des Herstellers der SLM (z. B. Füllung Faktor, Reflexionsvermögen oder Beugung Effizienz), die Größe der codierten Muster und die Art und Weise, an dem das Licht trifft auf, die SLM (Reflexion mit einem kleinen schlagkräftigen Winkel oder normalen Inzidenz mit einem Strahlteiler). An dieser Stelle kann der gemessenen Licht Gesamtwirkungsgrad unter den richtigen experimentellen Bedingungen, mehr als 30 % sein. Beachten Sie jedoch, dass diese leichte Gesamtwirkungsgrad nur durch den Einsatz von der SLM weniger als 50 % sein kann. Das Fehlen von zufälligen oder Diffusor-Elemente innerhalb der optischen Einrichtung ermöglicht den Abruf von Amplitude und Phase Muster ohne kohärente Lärm (Fleck). Andere wichtige Aspekte hinweisen sind die Nutzung eines direkten Kodifizierung Algorithmus anstatt iterativen Verfahren und seine Fähigkeit, willkürlich und unabhängige Amplitude und Phase Modulation der Frequenz (bis zu Zeit von der SLM aktualisieren Hunderte von Hertz nach den aktuellen Stand der Technik).
Im Prinzip Methode7 ist mit Eingang Ebene Wellen verwendet werden soll, aber es ist nicht darauf beschränkt. Beispielsweise wenn ein Gaußscher Strahl die SLM trifft, ist es möglich, seine Form der Bestrahlungsstärke am Ausgang des Systems durch Codierung eine Muster geeignet Amplitude in der SLM. Jedoch wie die Intensität des Strahls Ausgabe, die von der Eingabe Strahl an jeder transversale Position (X, y) nicht überschreiten darf, ist die Gestaltung der Amplitude durch Intensität Verluste entstanden durch einen teilweise destruktive Interferenz-Prozess durchgeführt.
Die Theorie unterstreicht die Codierung Methode7 ist wie folgt. Komplexes Feld vertreten in Form U(X,y)= A(X,y)eichφ()X,y( ) kann auch als umgeschrieben werden:
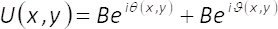 (1)
(1)
wo
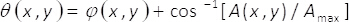 (2)
(2)
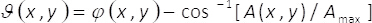 (3)
(3)
In Gleichungen 1-3, der Amplitude und Phase des zweidimensionalen komplexes Feld U(X,y) (X,y)ist gegeben durch Aund φ(X,y), beziehungsweise. Beachten Sie, die Bedingungen einermax (maximal A(X,y)) und B = einmax/2 hängen nicht von der transversalen Koordinaten (X,y). Aus der Theorie, wenn wir setzen einmax= 2, dann ist B =1. Daher das komplexe Feld U(X,y) auf einfache Weise erzielt werden, werden von der kohärenten Summe der gleichmäßige Wellen werdenichϑ()X,y( ) und Iθ ()X,y(). In der Praxis geschieht dies mit einer gemeinsamen Weg Interferometer besteht aus einem einphasig Element α(X,y), bei der Eingabe Ebene ein bildgebendes System platziert. Das Einphasen-Element wird erstellt, indem die räumliche multiplexing von Phase Begriffe ϑ(X,y)
und θ (X,y) mit Hilfe der zweidimensionalen binäre Gitterroste (Schachbrettmuster) M1(X,y) und M2(x,y) wie folgt
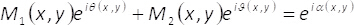 (4)
(4)
Daher
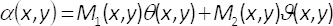 (5)
(5)
Diese binären Muster erfüllen die Bedingung M1(X,y) + M2(X,y) = 1. Beachten Sie, dass die Einmischung der gleichmäßige Wellen passieren kann, wenn wir nicht den Angaben in der Phase Elementα(x,y) mischen. In dem vorliegenden Verfahren erfolgt dies mithilfe eines räumlichen Filters alle Beugung Bestellungen aber die nullte einer blockieren. Auf diese Weise, nach der Filterung auf der Fourier-Ebene, das Spektrum H(u,V)= F{eIα()X,y()} der codierten Phase Funktion bezieht sich auf das Spektrum der komplexen Feldes F{U(X,y)} durch den Ausdruck
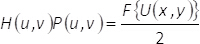 (6)
(6)
In GL. (6) (u,V) bezeichnen Koordinaten im Frequenzbereich, P(u,V) gilt für die räumliche Filter, während die Fourier-Transformation von einer bestimmten Funktion Θ(X,y) in der Form dargestellt wird F {Θ(X,y)}. Aus GL. (6) Es folgt, dass bei der Ausgabe-Ebene des imaging Systems, abgerufen am komplexen Feld URET(X,y), (ohne Rücksicht auf konstante Faktoren), ergibt sich aus der Faltung die vergrößerte und räumlich komplexes Feld U(X,y) mit der Fourier-Transformation von der Filtermaske rückgängig gemacht. Das heißt:
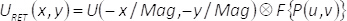 (7)
(7)
In GL. (7), Windung Betrieb ist gekennzeichnet durch das Symbol  , und der Begriff Mag steht für die Vergrößerung des imaging-System. Daher wird die Amplitude und Phase von U(X,y) voll und ganz auf der Ebene der Ausgabe, mit Ausnahme von gewissen Verlust an räumliche Auflösung durch die Faltung Betrieb abgerufen.
, und der Begriff Mag steht für die Vergrößerung des imaging-System. Daher wird die Amplitude und Phase von U(X,y) voll und ganz auf der Ebene der Ausgabe, mit Ausnahme von gewissen Verlust an räumliche Auflösung durch die Faltung Betrieb abgerufen.
Protokoll
1. codieren das komplexe Feld in ein Einphasen-Element
- Entnehmen Sie die technischen Spezifikationen der SLM seine räumlichen Auflösung (zum Beispiel 1920 Pixel X 1800 Pixel).
- Definieren und die gewünschte Amplitude A(X,y) und Phase φ(X,y) Muster als digitale Bilder zu generieren.
- Legen Sie die räumliche Auflösung der oben genannten Digitalbilder entspricht derjenigen der SLM-Anzeige.
- Oben genannten Digitalbilder in grau-Level-Formatierung gesetzt.
- Legen Sie die minimale und maximale Werte der Amplitude und Phase Bilder von 0 bis 255, und von - π/2, π/2, jeweils.
- Legen Sie einemax = 2 in Gleichungen 2 und 3, und Computer-generiert die Phase Muster ϑ(X,y) und θ(X,y) von ihnen.
- Computer generiert das Schachbrettmuster M1(X,y) und M2(X,y).
- Die räumliche Auflösung dieser Schachbrett-Muster entspricht derjenigen der SLM-Anzeige einstellen
- Um die Wirkung der Pixel Übersprechen zu verringern, erzeugen andere Paare Schachbrettmuster M1(X,y) und M2(X,y) konstruiert mit unterschiedlichen Pixelzellen mit einer Anzahl der Pixel erhöht (zum Beispiel: 2 x 2, 3 x 3 und 4 x 4 Pixelzellen usw.).
Achtung: Wenn die Pixel-Zelle zu erhöhen, muss die Gesamtzahl der Pixel mit Schachbrettmuster unverändert und die räumliche Auflösung der SLM gleich gehalten werden. Sicherstellen Sie, dass die endgültige Anzahl der Pixel aller Schachbrett Muster unverändert nach der Änderung der Pixelzellen.
- Computer generieren aus Gleichung 5 einphasig Element α(X,y).
Hinweis: Siehe Zusatzmaterial namens "MATLAB_code_1.m" für Verwandte Aufgaben auf Schritt 1 dieses Protokolls.
(2) Rekonstruktion von komplexen Feld
- Verwenden Sie einen kollimierten, linear polarisiert und räumlich kohärenter Laserstrahl als Lichtquelle.
- Verwenden Sie mindestens eine Phase nur SLM mit 2π einphasigen Modellreihe.
- Wenn nötig, verwenden Sie eine ordnungsgemäße Beam Expander die Größe des Balkens auf die Größe des SLM Displays anpassen.
- Wenn nötig, verwenden Sie eine optische Polarisator, Laser Beam Polarisation in horizontaler Richtung einzurichten. Dies ist in der Regel wichtig für den ordnungsgemäßen Betrieb der Phase nur geworden, die in der Regel modulieren die räumliche Phase des elektromagnetischen Feldes, das in horizontaler Richtung schwingen sollen, seine vertikale Komponenten unverändert zu halten.
- Um die SLM eine Phase-Muster zukommen lassen, folgen Sie standard Kommunikations-Protokolle der SLM-Herstellers zu verbinden und die SLM mit dem Computer zu steuern.
Hinweis: Gemeinsames Protokoll zu diesem Zweck beinhaltet die Nutzung der eine Eichkurve, die Werte im Bogenmaß (durch mathematische Operationen mit Winkeln) in Graustufen diejenigen, verwandeln die Steuerungselektronik der SLM schließlich in Spannungspegel umwandeln wird. Darüber hinaus wie die SLM als externes Gerät mit seinen eigenen Bildschirm Computer verbunden ist, ist eine Erweiterung von dem Computer-Bildschirm in der Regel notwendig, sowie eine richtige Programm die entsprechenden grauen Ebene Bilder zu diesem zusätzlichen Bildschirm senden. Ein Beispiel für diese Codes ist auch als Zusatzmaterial enthalten (bitte, siehe MATLAB_code_2.m). - Umsetzen eines optischen Systems von Bild und die Anzeige von der SLM in der Eingabe Ebene dieses Systems.
- Verwenden Sie eine refraktive Objektiv einer Brennweite f , um ein 2f 2f optische System zu konstruieren, (ein optisches System 4f gilt auch für diese Aufgabe). Im Einklang mit der erwarteten Ausgabegröße des komplexes Feld, Lichtstrahlbreite, Wellenlänge des Lichts und den verfügbaren physischen Raum beschäftigen Sie Objektiv/Objektive mit geeignet technische Daten (z. B. Beschichtung, Größe, Brennweite, etc.).
- Um die Position des Flugzeugs Ausgabe von imaging-System suchen, senden Sie die Phase Muster α(X,y) an die SLM und suchen Sie visuell das aufgenommene Bild (abhängig von der Position der Kamera) mit der besten Auflösung.
Achtung: Bei geringem Ausmaß Pixelzellen (z.B. 1 x 1 Pixel) und SLM Displays mit Pixel Breite von wenigen µm (z. B. 8 µm), kann nur Strahl Ausbreitung Interferenzen zwischen den codierten gleichmäßige Wellen, immer einen rekonstruierten Bilder produzieren ohne die kreisförmige Blende in der imaging-System. Verwenden Sie geringem Ausmaß Pixelzellen, um die Position der Output-Ebene zu finden. - Eine kreisförmige Iris mit variablem Durchmesser bei der Fourier-Ebene des optischen Systems und richten Sie der Mitte mit der Laser-Strahl-Fokus aus.
- Um die Größe der kreisförmigen Iris bei der Fourier-Ebene anzupassen, senden Sie die Phase Muster α(X,y) und suchen Sie visuell das aufgenommene Bild (je nach Durchmesser der kreisförmigen Iris) mit am besten räumlichen Auflösung.
Achtung: Bei Long-Größe Pixelzellen (z. B. 4 x 4 Pixel), die Interferenzen zwischen den codierten gleichmäßige Wellen im Grunde mit der räumlichen Filters erfolgt. Verwenden Sie Long-Größe Pixel Zelle, um die Größe der kreisförmigen Iris anzupassen. In diesem Protokoll werden die Begriffe geringem Ausmaß und Long-Größe die Anzahl der Pixel innerhalb einer Pixel-Zelle bezeichnet. Die oben genannten Störungen hängt jedoch auch die Pixelbreite. Beschäftigen Sie SLMs mit Pixel breiten gleich oder weniger als 8 µm.
- Senden Sie das graue Ebene Bild entspricht der Phase Element α(x,y) zu der SLM.
- Um den Crosstalk-Effekt zu minimieren, suchen Sie die beste Zelle Pixelgröße die ermöglichen das aufgenommene Bild mit höherer räumlicher Auflösung zu erreichen.
3. Messen Sie die rekonstruierte komplexe Feld
- Implementieren Sie die Polarisation-basierte Phasenverschiebung Technik8.
- Platzieren und ausrichten den Drehwinkel der ersten optischen Polarisator, befindet sich kurz vor der SLM (siehe Abbildung 2). Legen Sie den Drehwinkel der ersten Polarisator suchen Sie visuell die maximale und minimale Lichtdurchlässigkeit in der CCD-Kamera (platziert auf der Ebene der Ausgabe von der imaging-System), je nach Drehung der Polarisator. Notieren Sie sich die beiden entsprechenden Winkel der Polarisator. Den letzten Winkel der Polarisator, die zwischen die beiden vorherigen aufgezeichnet Winkel zu beheben.
- Platzieren und ausrichten den Drehwinkel der zweiten optischen Polarisator, befindet sich nach der Fourier-Ebene des imaging-System (siehe Abbildung 2). Legen Sie den Drehwinkel der zweiten Polarisator suchen Sie visuell die schärfsten und meist unscharfe Bilder in der CCD-Kamera (platziert auf der Ebene der Ausgabe von der imaging-System) nach dem Senden der Phase Muster α(x,y) an die SLM. Notieren Sie sich die beiden entsprechenden Winkel der Polarisator. Den letzte Winkel der zweiten Polarisator, die zwischen der vorherigen aufgezeichnet Winkel zu beheben.
- Notieren Sie die Interferogramme.
- Halten Sie die CCD-Kamera auf der Ebene der Ausgabe von der imaging-System.
- Um die erste Interferogramm aufzuzeichnen, die Phase Element α(X,y) eine Matrix von 0 Bogenmaß hinzu und senden Sie es an die SLM. Rekord entsprechende Bild ich1(X,y) mit dem CCD.
- Um die zweite Interferogramm aufzuzeichnen, die Phase Element α(X,y) eine Matrix von π/2 Bogenmaß hinzu und senden Sie es an die SLM. Rekord entsprechende Bild ich2(X,y) mit der CCD-Kamera.
- Um die dritte Interferogramm aufzuzeichnen, die Phase Element α(X,y) eine Matrix von π Bogenmaß hinzu und senden Sie es an die SLM. Rekord entsprechende Bild ich3(X,y) mit der CCD-Kamera.
- Um die vierte und letzte Interferogramm aufzuzeichnen, die Phase Element α(X,y) eine Matrix von 3π/2 Bogenmaß hinzu und senden Sie es an die SLM. Rekord entsprechende Bild ich4(X,y) mit der CCD-Kamera.
- Das komplexe Feld zu rekonstruieren.
Hinweis: Siehe Zusatzmaterial namens "MATLAB_code_3.m" für die damit verbundenen Aufgaben in diesem Punkt des Protokolls.- Abzurufen Sie die Amplitude der komplexen Feldes eineabgerufen(X,y) mithilfe des Ausdrucks
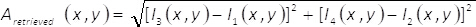 (8)
(8) - Abzurufen Sie die Phase der komplexen Feldes φabgerufen(X,y) mithilfe des Ausdrucks
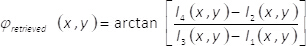 (9)
(9)
- Abzurufen Sie die Amplitude der komplexen Feldes eineabgerufen(X,y) mithilfe des Ausdrucks
Ergebnisse
Die räumliche Auflösung der Beschäftigten nur Phase SLM ist 1920 Pixel X 1080 Pixel mit einem Pixelabstand von 8 µm. Die ausgewählten Amplitude A(X,y) und Phase φ(X,y) die komplexen Feldes werden durch zwei verschiedene graue Ebene Bilder entsprechend der bekannten Lenna Bild (Amplitude Muster) und ein junges Mädchen definiert. Zunge (Phase Muster), herausragen bzw.. Im Allgemeinen sind für die Generierung der erforderlichen Mu...
Diskussion
In diesem Protokoll sind praktische Parameter wie die Pixelbreite der Phase nur SLM oder die Anzahl der Pixel Pixelzellen eines Computer-generierte Muster enthaltenen Eckpunkte die Codierungsmethode erfolgreich umzusetzen. In Schritten 1.2, 1.3 und 1.4 das Protokoll, je kürzer die Pixelbreite, desto besser die räumliche Auflösung der abgerufenen Amplitude und Phase Muster. Darüber hinaus wie die Kodifizierung in der SLM von abrupten Pixel für Pixel Phase Modulationen unerwartete Phasengänge (Pixel Übersprechen) en...
Offenlegungen
Die Autoren haben nichts preisgeben.
Danksagungen
Diese Forschung wurde unterstützt durch die Generalitat Valenciana (PROMETEO 2016-079), Universitat Jaume ich (UJI) (UJIB2016-19); und Ministerio de Economía y Competitividad (MINECO) (FIS2016-75618-R). Die Autoren sind sehr dankbar für die SCIC der Universitat Jaume I für die Verwendung der Femtosekunden-Laser.
Materialien
| Name | Company | Catalog Number | Comments |
| Achromatic Doublet | THORLABS | AC254-100-B-ML | Lens Diameter 25.4 mm, focal length 100 mm |
| Achromatic Galilean Beam Expander | THORLABS | GBE05-A | AR Coated: 400 - 650 nm |
| Basler camera | BASLER | avA1600-50gm GigE camera | sensor size 8.8 mm x 6.6 mm, pizel size 5.5 microns |
| Mounted Zero-Aperture Iris | THORLABS | ID12Z/M | Max Aperture 12 mm |
| Pellicle Beamsplitter | THORLABS | CM1-BP145B2 | 45:55 (R:T), Coating: 700 - 900 nm |
| PLUTO Spatial Light Modulator | HOLOEYE Photonics AG | NIR-II | Phase Only Spatial Light Modulator (Optimized for 700 -1000 nm) |
| Two thin film laser polarizers | EKSMA OPTICS | 420-0526M | material BK7, diameter 50 mm, wavelength 780-820 nm |
Referenzen
- Hsueh, C. K., Sawchuk, A. A. Computer-generated double-phase holograms. Applied Optics. 17 (24), 3874-3883 (1978).
- Arrizón, V. Complex modulation with a twisted-nematic liquid-crystal spatial light modulator: double-pixel approach. Optics Letters. 28 (15), 1359-1361 (2003).
- Arrizón, V., Ruiz, U., Carrada, R., González, L. A. Pixelated phase computer holograms for the accurate encoding of scalar complex fields. Journal of the Optical Society of America A. 24 (11), (2007).
- Shibukawa, A., Okamoto, A., Takabayashi, M., Tomita, A. Spatial cross modulation method using a random diffuser and phase-only spatial light modulator for constructing arbitrary complex fields. Optics Express. 22 (4), 3968-3982 (2014).
- Martínez-Fuentes, J. L., Moreno, I. Random technique to encode complex valued holograms with on axis reconstruction onto phase-only displays. Optics Express. 26 (5), 5875-5893 (2018).
- Clark, T. W., Offer, R. F., Franke-Arnold, S., Arnold, A. S., Radwell, N. Comparison of beam generation techniques using a phase only spatial light modulator. Optics Express. 24 (6), 6249-6264 (2016).
- Mendoza-Yero, O., Mínguez-Vega, G., Lancis, J. Encoding complex fields by using a phase-only optical element. Optics Letters. 39 (7), 1740-1743 (2014).
- Yamaguchi, I., Zhang, T. Phase-shifting digital holography. Optics Letters. 22 (16), 1268-1270 (1997).
- Shao, Y., et al. Addressable multiregional and multifocal multiphoton microscopy based on a spatial light modulator. Journal of Biomedical Optics. 17 (3), 030505 (2012).
- Mendoza-Yero, O., Carbonell-Leal, M., Mínguez-Vega, G., Lancis, J. Generation of multifocal irradiance patterns by using complex Fresnel holograms. Optics Letters. 43 (5), 1167-1170 (2018).
- Kuang, Z., et al. Diffractive Multi-beam Ultra-fast Laser Micro-processing Using a Spatial Light Modulator (Invited Paper). Chinese Journal of Lasers. 36 (12), 3093-3115 (2009).
- Kuang, Z., et al. High throughput diffractive multi-beam femtosecond laser processing using a spatial light modulator. Applied Surface Science. 255, 2284-2289 (2008).
Nachdrucke und Genehmigungen
Genehmigung beantragen, um den Text oder die Abbildungen dieses JoVE-Artikels zu verwenden
Genehmigung beantragenThis article has been published
Video Coming Soon
Copyright © 2025 MyJoVE Corporation. Alle Rechte vorbehalten