29.4 : Magnetic Field Due To A Thin Straight Wire
Consider an infinitely long straight wire carrying a current I. The magnetic field at point P at a distance a from the origin can be calculated using the Biot-Savart law.
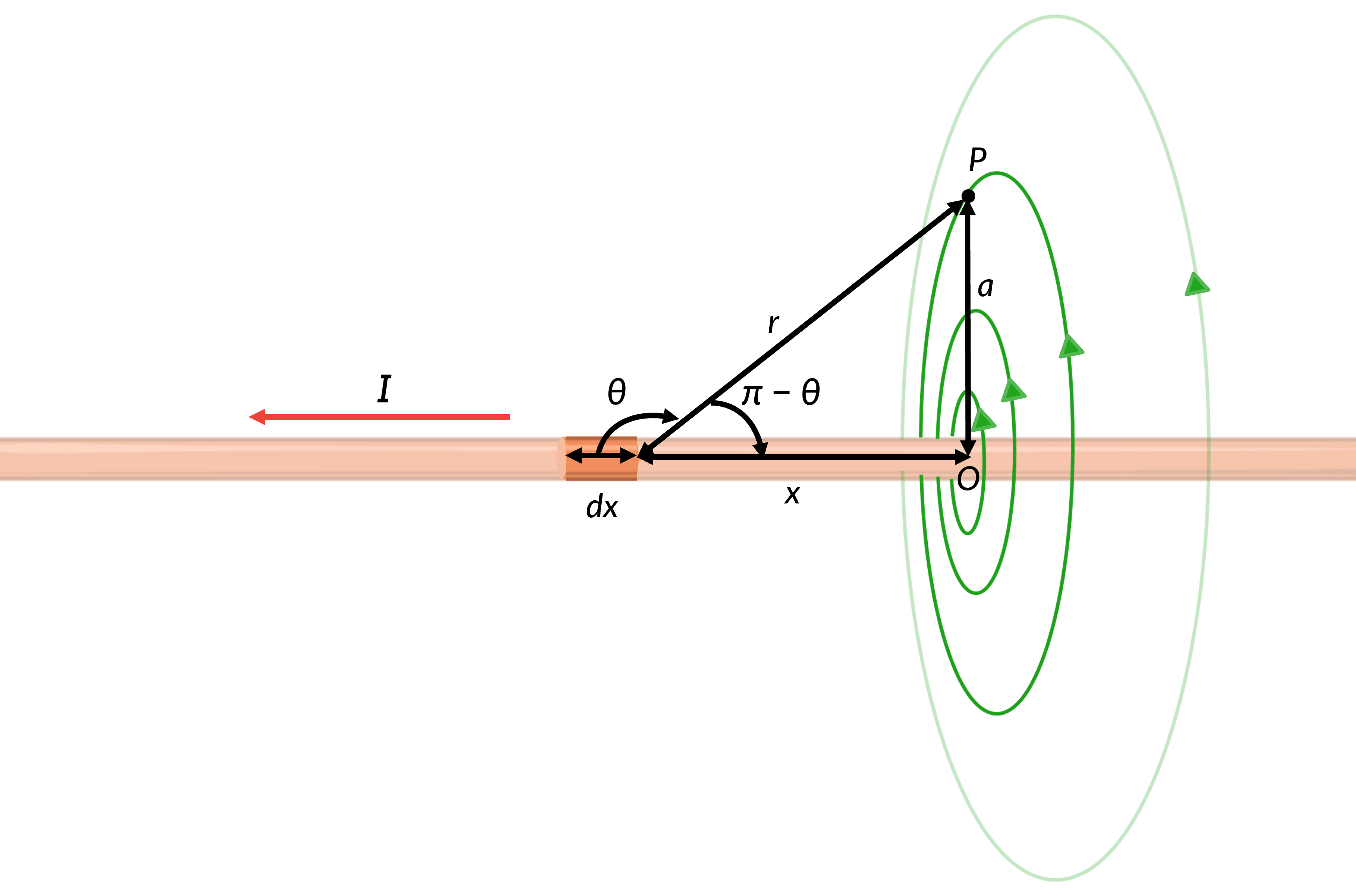
Consider a current element dx at a distance x from the origin. The current element makes an angle θ with the line joining dx and P. Using the Pythagorus theorum to express the distance between the current element and the point, the magnetic field due to the current element at point P can be estimated using Equation 1.
The wire is symmetrical about the origin. Hence, integrating Equation 1 within the limits of zero to infinity gives the equation for the magnetic field in terms of the current and the distance of point P from the wire.
The magnetic field lines of the infinite wire are circular and centered at the wire, and they are identical at every plane perpendicular to the wire. Since the intensity of the field decreases with the distance from the wire, the spacing of the field lines also increases correspondingly with distance.
The right-hand rule gives the direction of magnetic field lines. If the thumb points along the current, the fingers wrap around the wire in the same way as the magnetic field. Therefore, the field points into the page at point P. The magnetic fields due to all the current elements have the same direction.
From Chapter 29:

Now Playing
29.4 : Magnetic Field Due To A Thin Straight Wire
Sources of Magnetic Fields
4.7K Views

29.1 : Magnetic Field due to Moving Charges
Sources of Magnetic Fields
8.3K Views

29.2 : Biot-Savart Law
Sources of Magnetic Fields
5.8K Views

29.3 : Biot-Savart Law: Problem-Solving
Sources of Magnetic Fields
2.4K Views

29.5 : Magnetic Field Due to Two Straight Wires
Sources of Magnetic Fields
2.3K Views

29.6 : Magnetic Force Between Two Parallel Currents
Sources of Magnetic Fields
3.4K Views

29.7 : Magnetic Field Of A Current Loop
Sources of Magnetic Fields
4.3K Views

29.8 : Divergence and Curl of Magnetic Field
Sources of Magnetic Fields
2.7K Views

29.9 : Ampere's Law
Sources of Magnetic Fields
3.6K Views

29.10 : Ampere's Law: Problem-Solving
Sources of Magnetic Fields
3.5K Views

29.11 : Solenoids
Sources of Magnetic Fields
2.4K Views

29.12 : Magnetic Field of a Solenoid
Sources of Magnetic Fields
3.7K Views

29.13 : Toroids
Sources of Magnetic Fields
2.8K Views

29.14 : Magnetic Vector Potential
Sources of Magnetic Fields
523 Views

29.15 : Potential Due to a Magnetized Object
Sources of Magnetic Fields
253 Views
See More
Copyright © 2025 MyJoVE Corporation. All rights reserved