Un abonnement à JoVE est nécessaire pour voir ce contenu. Connectez-vous ou commencez votre essai gratuit.
Method Article
Façonner l’Amplitude et la Phase des rayons Laser à l’aide d’un modulateur de lumière Spatial Phase uniquement
Dans cet article
Résumé
Nous montrons comment coder le domaine complexe des faisceaux laser à l’aide d’un élément monophasé. Un interféromètre commun-chemin d’accès est utilisé pour mélanger les informations de phase affichées dans un modulateur de lumière spatial phase uniquement pour enfin récupérer le modèle de domaine complexe désirée à la sortie d’un système d’imagerie optique.
Résumé
Cet article vise à démontrer visuellement l’utilisation d’une méthode interférométrique pour le codage des champs complexes liés aux rayonnements laser cohérent. La méthode est basée sur la somme cohérente des deux vagues uniformes, précédemment codée en un seule phase modulateur spatial de lumière (SLM) par multiplexage spatial de leurs phases. Ici, le processus d’intervention est effectué par un filtrage spatial des fréquences de la lumière sur le plan de la transformée de Fourier de certain système d’imagerie. L’application correcte de cette méthode permet de phase arbitraire et amplitude informations à récupérer à la sortie du système optique.
C’est une technique de codage dans l’axe, et non hors de l’axe, avec un algorithme de traitement direct (pas une boucle itérative) et exemptes de bruit cohérent (moucheté). Le champ complex peut être exactement récupérée à la sortie du système optique, à l’exception d’un certain manque de résolution en raison du processus de filtrage de fréquence. La principale limite de la méthode pourrait venir de l’incapacité de fonctionner à des taux de fréquence plus élevées que la fréquence de rafraîchissement de la SLM. Les applications incluent, mais ne se limitent pas aux microscopes linéaire et non linéaire, faisceau façonnage ou laser micro-traitement des surfaces des matériaux.
Introduction
Presque toutes les applications de laser sont en relation étroite avec la direction du front d’onde optique de la lumière. Dans l’approximation paraxiale, le domaine complexe associé au rayonnement laser peut être décrite par deux termes, l’amplitude et la phase. Ayant autorité sur ces deux termes est nécessaire pour modifier le temporel et la structure spatiale des rayons laser à volonté. En général, l’amplitude et la phase d’un faisceau laser peuvent être correctement modifiés par plusieurs méthodes, y compris l’utilisation de composants optiques qui vont de lentilles simples en vrac, les séparateurs de faisceau et les miroirs vers des appareils plus complexes comme les miroirs déformables ou lumière spatiale modulateurs. Nous démontrons ici un procédé de codage et de reconstituer le domaine complexe des faisceaux cohérents, qui repose sur l’hologramme biphasé théorie1et l’utilisation d’un interféromètre de cheminement commun.
De nos jours, il existe une grande variété de méthodes pour coder les domaines complexes de laser poutres2,3,4,5. Dans ce contexte, certaines méthodes bien établies pour produire la modulation d’amplitude et de phase s’appuient sur l’utilisation des hologrammes numériques6. Un point commun à toutes ces méthodes est la nécessité de générer un décalage spatial pour séparer le faisceau de sortie souhaité de l’ordre zéro venant de la réflexion de la lumière à l’affichage SLM. Ces méthodes sont fondamentalement hors-axe (habituellement une demande de la première commande de diffraction de la grille), utilisant le réseau de phase non seulement d’encoder la phase, mais aussi d’introduire la modulation d’amplitude nécessaire. En particulier, la modulation d’amplitude est effectuée par spatialement abaisser la hauteur de la grille, qui dégrade clairement l’efficacité de diffraction. Le processus de reconstruction de hologramme obtient principalement une reconstitution approximative, mais pas exacte, de l’amplitude et la phase du champ complex désiré. Écarts entre la théorie et l’expérience semblent apparaître à partir d’un codage inexacte de l’information d’amplitude ainsi que d’autres questions expérimentales qui surviennent pendant le filtrage spatial de premier ordre de diffraction ou en raison des effets de pixellisation SLM. En outre, le profil d’intensité du faisceau d’entrée peut introduire des restrictions à la puissance de sortie.
En revanche, avec la méthode introduite7, tous les gestion de la lumière est effectuée dans l’axe, ce qui est très pratique du point de vue expérimental. En outre, il profite de considérer, dans l’approximation paraxiale, le champ complex associé de faisceaux laser comme une somme de deux ondes uniformes. Les informations d’amplitude sont synthétisée par l’interférence de ces vagues uniformes. Dans la pratique, cette ingérence est effectuée par un filtrage spatial des fréquences de la lumière sur le plan de la transformée de Fourier d’un système d’imagerie donné. Auparavant, les patrons de phase associés les vagues uniformes sont spatialement multiplexés et encodés dans une seule phase SLM (placé sur le plan de l’entrée de ce système d’imagerie). Par conséquent, la configuration de l’ensemble optique peut être considérée comme un interféromètre commun-chemin (très robuste contre les vibrations mécaniques, les changements de température ou distorsions optiques). Veuillez noter que le processus d’interférence susmentionné est par ailleurs possible l’aide des autres dispositions optiques : avec un couple de MSL phase seule correctement placé dans un interféromètre typique de deux bras ou lors de l’encodage dans l’ordre les deux phases patrons dans le MLS (précédente introduction d’un miroir de renvoi dans la configuration optique). Dans les deux cas, il n’y a aucune nécessité de filtrage spatial et par conséquent sans perte de résolution spatiale, au détriment de l’accroissement de la complexité du système optique, ainsi que le processus d’alignement. Ici, il convient également de souligner que grâce à cette méthode de codage, l’éventail complet du champ complex désiré peut être récupérée exactement sur le plan de Fourier, après filtrage de tous les ordres de diffraction mais le zéro un.
En revanche, l’efficacité de la méthode dépend de plusieurs facteurs : les spécifications du fabricant de la SLM (p. ex., fill factor, réflectivité ou diffraction efficacité), la taille du modèle codé et la façon à laquelle la lumière empiète sur le SLM (réflexion avec un petit angle de frappe, ou l’incidence normale à l’aide d’un séparateur de faisceau). À ce stade, dans de bonnes conditions expérimentales, l’efficacité lumineuse totale mesurée peut être plus de 30 %. Toutefois, Notez que l’efficacité lumineuse juste en raison de l’utilisation de la SLM pouvant être inférieure à 50 %. L’absence de hasard ou d’éléments de diffuseur dans l’optique installation permet la récupération des modèles de phase et d’amplitude sans bruit cohérent (moucheté). D’autres aspects importants à souligner sont l’utilisation d’un algorithme de codification directe plutôt que les procédures itératives et sa capacité d’exécuter amplitude arbitraire et indépendante et modulation de phase à la fréquence de rafraîchissement temps de la SLM (jusqu'à centaines de hertz selon la technologie actuelle).
En principe, la méthode7 est destiné à être utilisé avec des ondes planes d’entrée, mais il n’est pas limité à cela. Par exemple, si un faisceau gaussien est de frapper le SLM, il est possible de modifier sa forme de rayonnement à la sortie du système en codant un modèle adapté amplitude dans la MLS. Toutefois, comme l’intensité du faisceau de sortie ne peut dépasser celle du faisceau d’entrée à n’importe quelle position transversale (x, y), la mise en forme de l’amplitude est effectuée par des pertes d’intensité émis par un processus d’interférence destructive partiellement.
La théorie soulignant le codage de la méthode7 est la suivante. N’importe quel champ complexe représenté sous la forme U(x,y)= A(x,y)ej’aiφ()x,y) peut être aussi réécrit sous la forme :
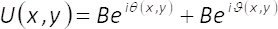 (1)
(1)
où
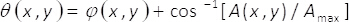 (2)
(2)
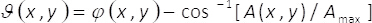 (3)
(3)
Dans les équations 1-3, l’amplitude et la phase du complexe bidimensionnel champ U(x,y)est donnée par A(x,y) et φ(x,y), respectivement. Notez que, en termes unmax (maximum A(x,y)) et B = unmax/2 ne dépendent pas les transversales coordonnées (x,y). De la théorie, si nous fixons unmax= 2, puis B =1. Par conséquent, le champ complex U(x,y) peut être obtenue, d’une manière simple, de la somme cohérente des vagues uniformes êtrej’aiϑ(x,y) et être iθ ()x,y). Dans la pratique, ceci est accompli avec un interféromètre de chemin commun composé d’une phase unique élément α(x,y), placé dans le plan d’entrée d’un système d’imagerie. L’élément monophasé est construit par multiplexage spatial de la phase termes ϑ(x,y)
et θ (x,y) à l’aide de grilles binaires à deux dimensions (modèles de damier) M1(x,y) et M2(x,y) comme suit
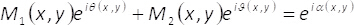 (4)
(4)
par conséquent,
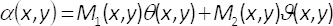 (5)
(5)
Ces modèles binaires remplissent la condition M1(x,y) + M2(x,y) = 1. Notez que, l’interférence des ondes uniformes ne peut pas arriver si nous ne mélangez pas les informations contenues dans les éléments en phaseα(x,y). Dans la présente méthode, ceci est effectué en utilisant un filtre spatial capable de bloquer tous les ordres de diffraction mais le zéro un. De cette manière, après le processus de filtrage sur le plan de Fourier, spectre H(u,v)= F{eiα()x,y)} de la phase de codage fonction est liée au spectre du champ complex F{U(x,y)} par l’expression
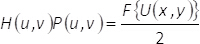 (6)
(6)
Dans l’équation (6), (u,v) indiquer les coordonnées dans le domaine fréquentiel, P(u,v) détient pour le filtre spatial, alors que la transformée de Fourier d’une fonction donnée Θ(x,y) est représentée sous la forme F {Θ(x,y)}. De l’équation (6), il s’ensuit que, sur le plan de sortie du système d’imagerie, le champ complex consulté URET(x,y), (sans tenir compte de facteurs constants), est donnée par le produit de convolution de l’agrandie et dans l’espace inversée, domaine complexe U(x,y) avec la transformation de Fourier du masque filtre. C'est :
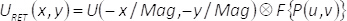 (7)
(7)
Dans l’équation (7), l’opération de convolution est désignée par le symbole  et le terme Mag représente le grossissement de l’appareil d’imagerie. Par conséquent, l’amplitude et la phase U(x,y) est entièrement récupéré sur le plan de sortie, à l’exception d’un certain manque de résolution spatiale en raison de l’opération de convolution.
et le terme Mag représente le grossissement de l’appareil d’imagerie. Par conséquent, l’amplitude et la phase U(x,y) est entièrement récupéré sur le plan de sortie, à l’exception d’un certain manque de résolution spatiale en raison de l’opération de convolution.
Access restricted. Please log in or start a trial to view this content.
Protocole
1. codage du champ Complex dans un élément monophasé
- De la fiche technique de la SLM, trouve sa résolution spatiale (par exemple 1920 pixels x 1800 de pixels).
- Définir et générer l’amplitude souhaitée A(x,y) et les modèles de phase φ(x,y) sous forme d’images numériques.
- Définissez la résolution spatiale de précitée images numériques égale à celle de l’affichage SLM.
- La valeur susmentionnée images numériques format niveaux gris.
- Définissez les valeurs minimales et maximales des images amplitude et de phase de 0 à 255 et de - π/2, π/2, respectivement.
- Définir unmax = 2 dans les équations 2 et 3 et ordinateur-générer la phase patterns ϑ(x,y) et θ(x,y) de leur part.
- Ordinateur génère les patrons damier M1(x,y) et M2(x,y).
- La résolution spatiale de ces modèles de damier la valeur égale à celle de l’affichage SLM.
- Pour réduire l’effet de la diaphonie pixel, générer d’autres paires de modèles damier M1(x,y) et M2(x,y) construit avec des cellules de pixel différent ayant une a augmenté le nombre de pixels (par exemple : cellules de pixels 2 x 2, 3 x 3 et 4x4, etc.).
Attention : Lors de l’augmentation de la cellule de pixel, le nombre total de pixels de motifs damier doit demeurer inchangés et est égale à la résolution spatiale de la SLM. Veiller à ce que final nombre de pixels de tous les modèles de damier reste inchangé après avoir modifié leurs cellules de pixel.
- Ordinateur génère la phase unique élément α(x,y) de l’équation 5.
Remarque : Voir matériel supplémentaire nommé « MATLAB_code_1.m » pour les tâches connexes à l’étape 1 du présent protocole.
2. Reconstruction du champ complexe
- Utiliser un faisceau laser de collimaté, linéaire polarisée et cohérente dans l’espace comme une source de lumière.
- Utiliser une seule phase SLM au moins gamme phase 2π.
- Si nécessaire, utiliser un expandeur bon faisceau pour ajuster la taille du faisceau à la taille de l’écran SLM.
- Lorsque cela est nécessaire, utiliser un polariseur optique pour définir la polarisation du faisceau laser sur la direction horizontale. C’est généralement important pour le bon fonctionnement de phase seule MSL, qui sont généralement conçus pour moduler la phase spatiale du champ électromagnétique qui oscillent dans le sens horizontal, gardant inchangées ses composantes verticales.
- Pour envoyer un modèle de phase à la SLM, suivre les protocoles de communication standard donnés par le fabricant de la SLM pour se connecter et contrôler le SLM avec l’ordinateur.
Remarque : Le protocole commun à cette fin comprend l’utilisation d’une courbe d’étalonnage pour transformer les valeurs en radians (en raison des opérations mathématiques avec angles) en niveau de gris ceux, dont l’unité de contrôle électronique de la SLM permet enfin de convertir en niveaux de tension. En outre, comme le SLM est connecté à l’ordinateur comme un périphérique externe avec son propre écran, une extension de l’écran d’ordinateur est habituellement nécessaire, en plus d’un programme approprié d’envoyer les images de niveau gris correspondants à cet écran supplémentaire. Un exemple de ces codes est également inclus dans le matériel supplémentaire (s’il vous plaît, voir MATLAB_code_2.m). - Mettre en place un système optique de l’image et mettre l’affichage de la SLM dans le plan d’entrée de ce système.
- Utiliser une lentille réfractive une longueur focale f pour construire un système optique de l’image def 2f x 2 (un système optique 4f est également valable pour cette tâche). Selon la taille de la sortie attendue de la matière complexe, largeur, longueur d’onde de la lumière et l’espace physique disponible, emploient la lentille/lentilles avec des spécifications techniques adaptées (par exemple, revêtement, taille, longueur focale, etc.).
- Pour trouver la position de l’avion de sortie du système d’imagerie, envoyer les modèle en phase α(x,y) à la SLM et de rechercher visuellement l’image enregistrée (en fonction de la position de la caméra) avec la meilleure résolution spatiale.
Attention : Dans le cas de petites dimensions pixel des cellules (par exemple, 1 x 1 pixel) et SLM affiche une largeur de pixel de quelques microns (par exemple, 8 µm), seul faisceau propagation peut produire interférence entre les ondes uniformes codés, faire une images reconstruites sans inclure l’iris circulaire dans le système d’imagerie. Cellules de petites dimensions pixel permet de localiser la position de l’avion de sortie. - Placer un iris circulaire de diamètre variable sur le plan de la transformée de Fourier du système optique et aligner son centre avec celle de la mise au point du faisceau laser.
- Pour ajuster la taille de l’iris circulaire sur le plan de Fourier, envoyer les modèle en phase α(x,y) et avoir l’apparence de l’image enregistrée (selon le diamètre de l’iris circulaire) avec la meilleure résolution spatiale.
Attention : Dans le cas des pixels de long-taille des cellules (par exemple, 4 x 4 pixels), l’interférence entre les ondes uniformes codés est effectué essentiellement avec le filtre spatial. Utilisez long-taille pixel cellule pour ajuster la taille de l’iris circulaire. Dans le présent protocole, les termes petites dimensions et long-taille portent le nombre de pixels contenus dans une cellule de pixel. Toutefois, l’intervention susmentionnée dépend aussi de la largeur en pixels. Emploient MSL avec largeurs de pixel égales ou inférieure à 8 µm.
- Envoyer l’image grise de niveau correspondant à la phase élément α(x,y) à la SLM.
- Pour minimiser l’effet de crosstalk, recherchez la meilleure taille de cellule de pixel qui permettent la réalisation de l’image enregistrée avec une résolution spatiale plus élevée.
3. mesurer le champ Complex reconstruit
- Mettre en œuvre les déphaseurs axée sur la polarisation technique8.
- Placer et aligner l’angle de rotation de la premier polariseur optique, situé juste avant le SLM (voir Figure 2). Pour définir l’angle de rotation de la premier polariseur, recherchez visuellement la transmittance maximale et minimale de la caméra CCD (placée sur le plan de sortie de l’appareil d’imagerie), selon la rotation du polariseur. Notez les deux angles correspondants du polariseur. Fixer l’angle final du polariseur à celle qui sépare les deux angles antérieurs enregistrés.
- Placer et aligner l’angle de rotation de la deuxième polariseur optique, situé après le plan de Fourier du système d’imagerie (voir Figure 2). Pour définir l’angle de rotation de la deuxième polariseur, avoir apparence pour les images plus nettes et plus floues de la caméra CCD (placé sur le plan de sortie de l’appareil d’imagerie) après l’envoi de la phase modèle α(x,y) à la SLM. Notez les deux angles correspondants du polariseur. Fixer l’angle final de la deuxième polariseur à celle qui sépare les angles antérieurs enregistrés.
- Enregistrer les interférogrammes.
- Garder la caméra CCD sur le plan de sortie du système d’imagerie.
- Pour enregistrer la première interférogramme, ajoutez une matrice de 0 radian à la phase élément α(x,y) et l’envoyer à la SLM. Enregistrement image correspondante j’ai1(x,y) avec la CDC.
- Pour enregistrer le deuxième interférogramme, ajouter une matrice de π/2 radians pour les éléments en phase α(x,y) et l’envoyer à la SLM. Enregistrement image correspondante j’ai2(x,y) avec la caméra CCD.
- Pour enregistrer le troisième interférogramme, ajoutez une matrice de radians π à la phase élément α(x,y) et l’envoyer à la SLM. Enregistrement image correspondante j’ai3(x,y) avec la caméra CCD.
- Pour enregistrer le quatrième et dernier interférogramme, ajouter une matrice de 3π/2 radians pour les éléments en phase α(x,y) et envoyez-le à la SLM. Enregistrement image correspondante j’ai4(x,y) avec la caméra CCD.
- Reconstruire le champ complex.
Remarque : Voir matériel supplémentaire nommé « MATLAB_code_3.m » pour les tâches connexes sur ce point du protocole.- Récupérer l’amplitude du champ complex unrécupérée(x,y) en utilisant l’expression
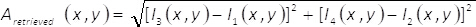 (8)
(8) - Récupérer la phase du champ complexe φrécupérée(x,y) en utilisant l’expression
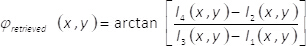 (9)
(9)
- Récupérer l’amplitude du champ complex unrécupérée(x,y) en utilisant l’expression
Access restricted. Please log in or start a trial to view this content.
Résultats
La résolution spatiale de la SLM phase uniquement salarié est 1920 pixels x 1080 de pixels, avec un terrain de pixel de 8 µm. Les sélectionnés d’amplitude A(x,y) et la phase φ(x,y) du champ complex sont définies par deux images différentes de niveau gris correspondant à l’image de la bien connue de Lenna (modèle d’amplitude) et une jeune fille qui sort sa langue (modèle de phase), respectivement. En général, pour une...
Access restricted. Please log in or start a trial to view this content.
Discussion
Dans ce protocole, paramètres pratiques comme la largeur en pixels de la SLM phase seule ou le nombre de pixels contenus dans les cellules de pixel d’un schéma de synthèse sont des points clés à mettre en œuvre la méthode de codage. En étapes, 1.2, 1.3 et 1.4 du protocole, le plus court la largeur en pixels, plus la résolution spatiale des modèles de phase et d’amplitude récupérées. En outre, comme la codification dans le MLS de modulations de phase abruptes pixel à pixel peut provenir des réponses ina...
Access restricted. Please log in or start a trial to view this content.
Déclarations de divulgation
Les auteurs n’ont rien à divulguer.
Remerciements
Cette recherche a été financée par la Generalitat Valenciana (2016 PROMETEO-079), Universitat Jaume I (UJI) UJIB2016 (19) ; et Ministerio de Economía y Competitividad (MINECO) (FIS2016-75618-R). Les auteurs sont très reconnaissants à la SCIC de la Universitat Jaume I pour l’utilisation du laser femtoseconde.
Access restricted. Please log in or start a trial to view this content.
matériels
| Name | Company | Catalog Number | Comments |
| Achromatic Doublet | THORLABS | AC254-100-B-ML | Lens Diameter 25.4 mm, focal length 100 mm |
| Achromatic Galilean Beam Expander | THORLABS | GBE05-A | AR Coated: 400 - 650 nm |
| Basler camera | BASLER | avA1600-50gm GigE camera | sensor size 8.8 mm x 6.6 mm, pizel size 5.5 microns |
| Mounted Zero-Aperture Iris | THORLABS | ID12Z/M | Max Aperture 12 mm |
| Pellicle Beamsplitter | THORLABS | CM1-BP145B2 | 45:55 (R:T), Coating: 700 - 900 nm |
| PLUTO Spatial Light Modulator | HOLOEYE Photonics AG | NIR-II | Phase Only Spatial Light Modulator (Optimized for 700 -1000 nm) |
| Two thin film laser polarizers | EKSMA OPTICS | 420-0526M | material BK7, diameter 50 mm, wavelength 780-820 nm |
Références
- Hsueh, C. K., Sawchuk, A. A. Computer-generated double-phase holograms. Applied Optics. 17 (24), 3874-3883 (1978).
- Arrizón, V. Complex modulation with a twisted-nematic liquid-crystal spatial light modulator: double-pixel approach. Optics Letters. 28 (15), 1359-1361 (2003).
- Arrizón, V., Ruiz, U., Carrada, R., González, L. A. Pixelated phase computer holograms for the accurate encoding of scalar complex fields. Journal of the Optical Society of America A. 24 (11), (2007).
- Shibukawa, A., Okamoto, A., Takabayashi, M., Tomita, A. Spatial cross modulation method using a random diffuser and phase-only spatial light modulator for constructing arbitrary complex fields. Optics Express. 22 (4), 3968-3982 (2014).
- Martínez-Fuentes, J. L., Moreno, I. Random technique to encode complex valued holograms with on axis reconstruction onto phase-only displays. Optics Express. 26 (5), 5875-5893 (2018).
- Clark, T. W., Offer, R. F., Franke-Arnold, S., Arnold, A. S., Radwell, N. Comparison of beam generation techniques using a phase only spatial light modulator. Optics Express. 24 (6), 6249-6264 (2016).
- Mendoza-Yero, O., Mínguez-Vega, G., Lancis, J. Encoding complex fields by using a phase-only optical element. Optics Letters. 39 (7), 1740-1743 (2014).
- Yamaguchi, I., Zhang, T. Phase-shifting digital holography. Optics Letters. 22 (16), 1268-1270 (1997).
- Shao, Y., et al. Addressable multiregional and multifocal multiphoton microscopy based on a spatial light modulator. Journal of Biomedical Optics. 17 (3), 030505(2012).
- Mendoza-Yero, O., Carbonell-Leal, M., Mínguez-Vega, G., Lancis, J. Generation of multifocal irradiance patterns by using complex Fresnel holograms. Optics Letters. 43 (5), 1167-1170 (2018).
- Kuang, Z., et al. Diffractive Multi-beam Ultra-fast Laser Micro-processing Using a Spatial Light Modulator (Invited Paper). Chinese Journal of Lasers. 36 (12), 3093-3115 (2009).
- Kuang, Z., et al. High throughput diffractive multi-beam femtosecond laser processing using a spatial light modulator. Applied Surface Science. 255, 2284-2289 (2008).
Access restricted. Please log in or start a trial to view this content.
Réimpressions et Autorisations
Demande d’autorisation pour utiliser le texte ou les figures de cet article JoVE
Demande d’autorisationThis article has been published
Video Coming Soon