酸は、反応で与えることのできる1分子あたりのプロトン数によって分類されます。HCl、HNO3、HCNなど、電離可能な水素原子を1分子あたり1つ含む酸を一価の酸と呼びます。これらの酸と水との反応は、
| 一価の酸: 水との反応 |
| HCl (aq) + H2O (l) ⟶ H3O+ (aq) + Cl− (aq) |
| HNO3 (aq) + H2O (l) ⟶ H3O+ (aq) + NO3− (aq) |
| HCN (aq) + H2O (l) ⇌ H3O+ (aq) + CN− (aq) |
酢酸(CH3CO2H)は4つの水素原子を含んでいますが、カルボキシル基(COOH)の水素原子のみが塩基と反応するため、一価の塩基として作用します。
同様に、一価の塩基は、1つのプロトンを受容する塩基です。
二価の酸は1分子あたり2つの電離可能な水素原子を含んでおり、電離は2段階で起こります。1段階目の電離の方が2段階目の電離よりも必ず大きくなります。例えば、強酸である硫酸は次のように電離します。
| 二価の酸: 硫酸 (H2SO4) | ||
| 1段階目の電離 | H2SO4 (aq) + H2O (l) ⇌ H3O+ (aq) + HSO4− (aq) | Ka1 = more than 102; complete dissociation |
| 2段階目の電離 | HSO4− (aq) + H2O (l) ⇌ H3O+ (aq) + SO42− (aq) | Ka2 = 1.2 × 10−2 |
この段階的な電離プロセスは、すべての多価酸で起こります。炭酸(H2CO3)は、弱い二価酸の一例です。炭酸の1段階目の電離では、少量のヒドロニウムイオンと炭酸水素イオンが生成されます。
1段階目の電離: H2CO3 (aq) + H2O (l) ⇌ H3O+ (aq) + HCO3− (aq)
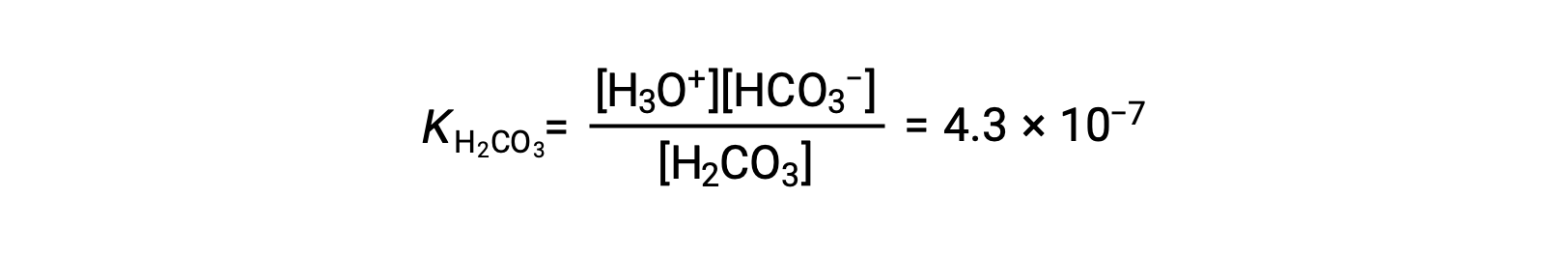
The bicarbonate ion can also act as an acid. It ionizes and forms hydronium ions and carbonate ions in even smaller quantities.
2段階目の電離: HCO3− (aq) + H2O (l) ⇌ H3O+ (aq) + CO32− (aq)
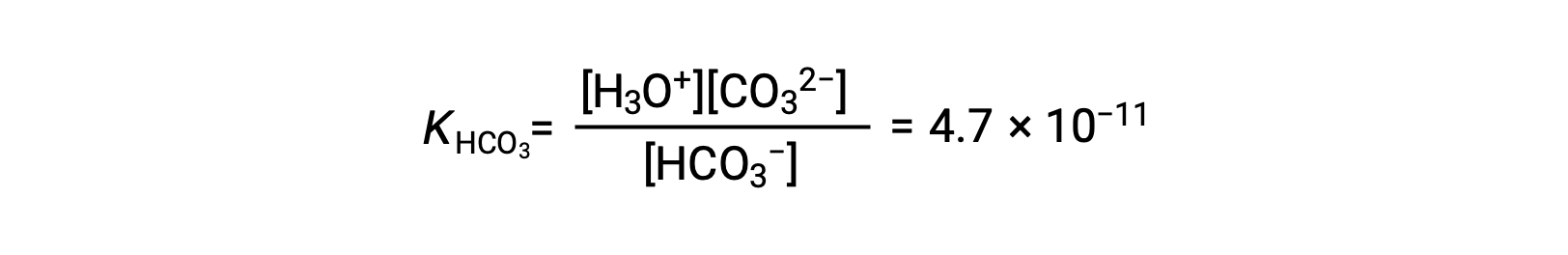
KH2CO3はKHCO3−よりも104も大きいので、主にH2CO3が溶液中のヒドロニウムイオンを生成します。つまり、H2CO3がイオン化してできたHCO3はほとんどイオン化せず、ヒドロニウムイオン(および炭酸イオン)を与え、H3O+とHCO3− は、H2CO3の純粋な水溶液中では実質的に等しくなります。
弱い二価の酸における1段階目の電離定数が2段階目の電離定数よりも少なくとも20倍以上大きい場合、1段階目の電離を別個に扱うのが適切です。その後、得られた濃度を後続の電離に起因する種の濃度計算に用います。この方法を以下の例題で示します。
二価の酸の電離
“炭酸水”には、口にすることができる程度の量の二酸化炭素が溶解しています。CO2が水と反応して炭酸(H2CO3)を生成するため、溶液は酸性となります。初期濃度[H2CO3]が0.033であるとき、飽和CO2溶液中における[H3O+]、[HCO3−]、[CO32−]の濃度はそれぞれいくらでしょうか?
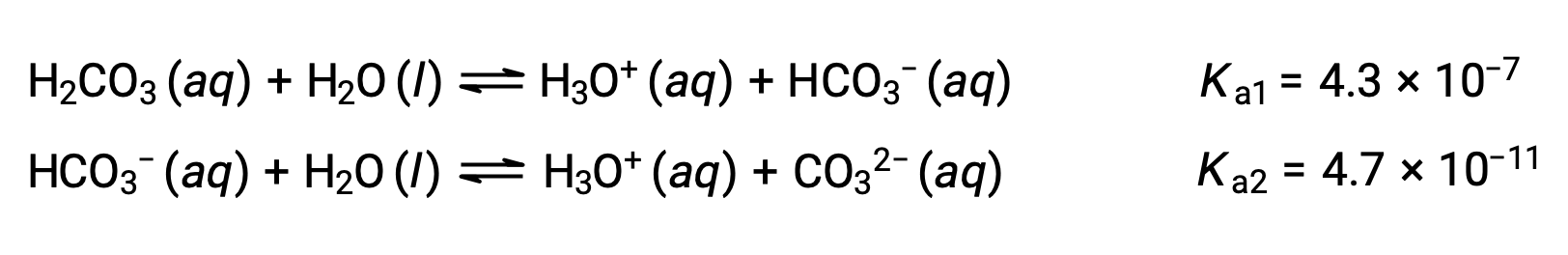
解離定数が示すように、H2CO3はHCO3−よりもはるかに強い酸であるため、段階的な電離反応は個別に扱ってもよいと考えられます。
| H2CO3 (aq) | H3O+ (aq) | HCO3− (aq) | |
| 初期濃度 (M) | 0.033 | ~0 | 0 |
| 濃度変化 (M) | −x | +x | +x |
| 平衡濃度 (M) | 0.033 − x | x | x |
この平衡濃度を平衡式に代入すると、
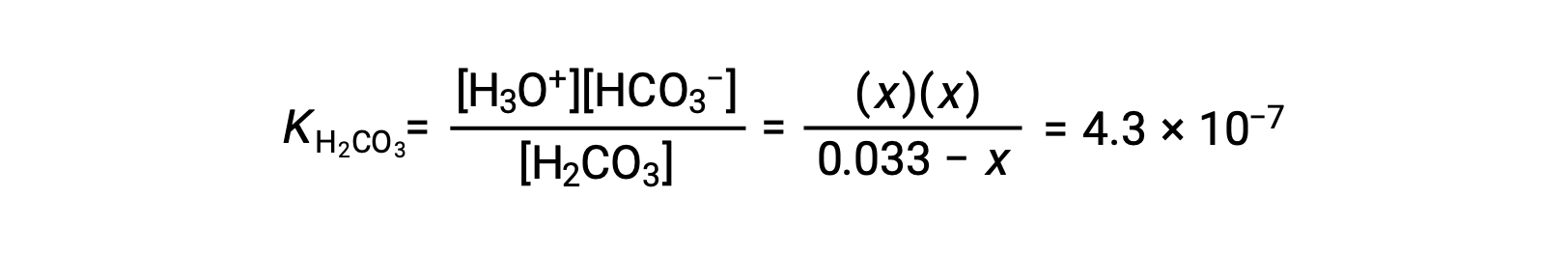
Assuming x << 0.033 となり、簡略化した式を解くと、
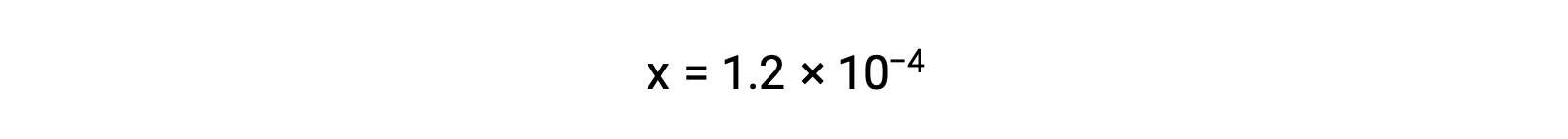
ICE表では、xは炭酸水素イオンの物質量とヒドロニウムイオンの物質量に等しいと定義されています。
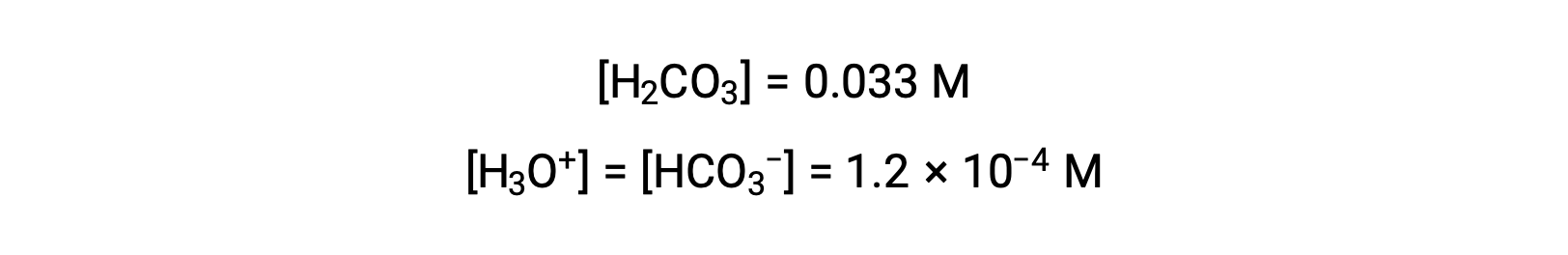
上記で計算した炭酸水素イオン濃度を用いて、2回目のイオン化も同様の平衡計算を行う: HCO3− (aq) + H2O (l) ⇌ H3O+ (aq) + CO32− (aq)
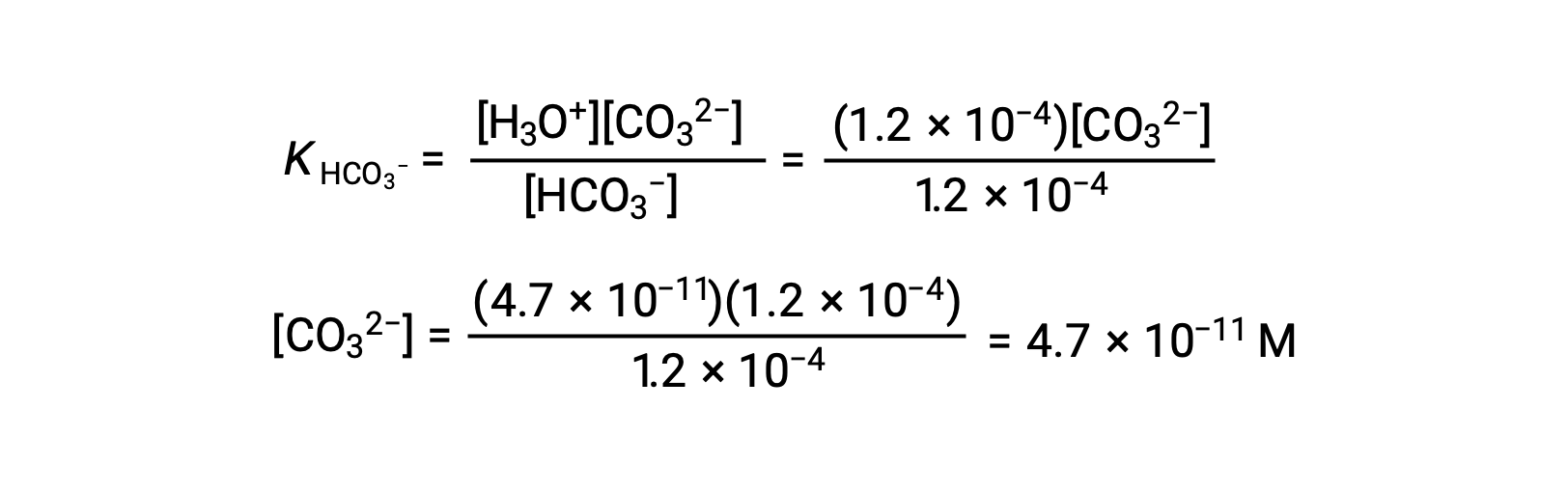
まとめ: 平衡において、 [H2CO3] = 0.033 M; [H3O+] = 1.2 × 10−4; [HCO3−] = 1.2 × 10−4 M; and [CO32−] = 4.7× 10−11 M.
三価の酸とは、電離可能なH原子を3つ持つ酸のことです。リン酸はその一例です。:
| 三価の酸: リン酸(H3PO4) | ||
| 1段階目の電離 | H3PO4 (aq) + H2O (l) ⇌ H3O+ (aq) + H2PO4− (aq) | Ka1 = 7.5 × 10−3 |
| 2段階目の電離 | H2PO4− (aq) + H2O (l) ⇌ H3O+ (aq) + HPO42− (aq) | Ka2 = 6.2 × 10−8 |
| 3段階目の電離 | HPO42− (aq) + H2O (l) ⇌ H3O+ (aq) + PO43− (aq) | Ka3 = 4.2 × 10−13 |
二価の酸の例のように、連続した電離反応は前段階も小さくなるため、酸解離定数の値は段階とともに減少していきます。これは多価酸の一般的な特徴で、連続する解離定数は約105から106の桁で異なることがよく知られています。
この3段階の電離反応は、H3PO4の溶液中の平衡濃度の計算を複雑にしているように見えるかもしれません。。しかし、連続する解離定数は、105から106の桁で異なるため、電離反応に伴うわずかな濃度変化にも大きな違いがあます。そのため、上記の例のように、数学的に単純化された仮定やプロセスを用いることができます。多価塩基は2つ以上の水素イオンを受け取ることができます。下図のように、炭酸イオンは2つのプロトンを受け取ることができるため、二価塩基の例となります。多価酸の場合と同様に、解離定数は電離ステップに応じて減少することに注意する必要があます。多価塩基の平衡計算は、多価酸の場合と同様に行うことが出来ます。
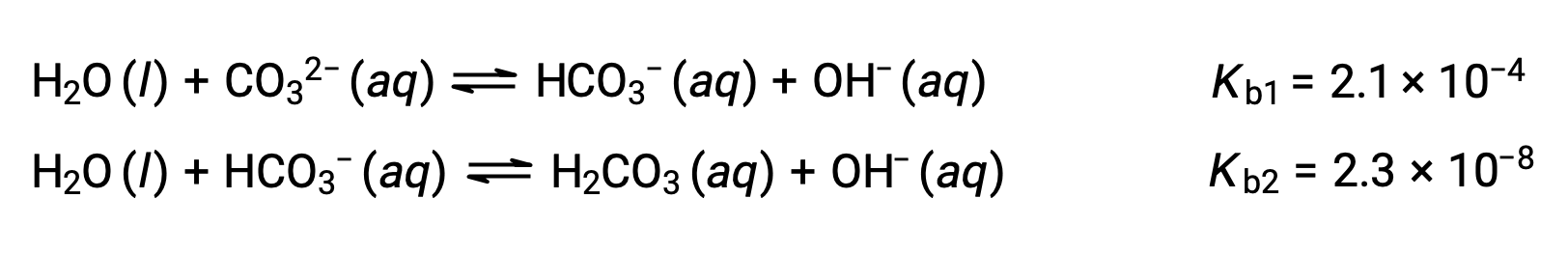
上記の文章は以下から引用した。 Openstax, Chemistry 2e, Section 14.5: Polyprotic Acids.
Copyright © 2023 MyJoVE Corporation. All rights reserved