フーリエ ベース回折分析のライブの線虫

要約

本稿では、遠視野の回折の署名を使用して別の線虫を区別する方法について説明します。連続波レーザーを使用して単一の場所に一時的なフラウンホーファー回折の署名に関連付けられている周波数を平均することによって 139 の野生型および 108「ローラー」 c. の elegansの歩行を比較します。

要約

本稿では、一時的な遠視野の回折の署名を使用して線虫を分類する方法について説明します。1 つのc. の elegansは光キュベット内の水柱で中断されます。632 nm 連続波 HeNe レーザーがフロント面の鏡を使用してキュベットを介して送られます。旅キュヴェットを光が通過した後、少なくとも 20 〜 30 cm のかなりの距離により有用な遠方界 (フラウンホーファー) 回折パターンになります。線虫とリアルタイムで回折パターンの変化は、レーザー ビーム内で泳ぐ。フォト ダイオードは、回折パターンの中心から外れてが配置されます。フォト ダイオードからの電圧信号をリアルタイムに観察し、デジタル ・ オシロ スコープを使用して記録しました。139 の野生型および 108「ローラー」 c. の elegansのこのプロセスが繰り返されます。野生型のワームは、ソリューションの急速な振動パターンを表わします。「ローラー」ワーム滑らかな歩行を妨げるクチクラの重要なコンポーネントの突然変異があります。彩度と非アクティブの自由ではない時間間隔は破棄されます。各平均の相対強度を比較する最大除算する実用的です。各ワームのための信号は、各ワームの周波数パターンが現れるようにフーリエ変換です。ワームの種類ごとに信号の平均です。野生型と「ローラー」線虫の平均のフーリエ スペクトルとはまったく違うとフーリエ解析を用いた 2 つの別のワーム系統の動的ワーム形状を区別できることを明らかにします。各ワームのひずみのフーリエ スペクトルと一致歩行瞬間に対応する 2 つの異なるバイナリ ワーム形状を用いた近似モデル。実際、モデル化されたワームの平均頻度分布の封筒は、モデル データに一致するを確認します。このメソッドは、すべての微生物はそのユニークなフーリエ スペクトルを持っている多くのミクロ種のフーリエ分析のためのベースラインとして使用できます。

概要

このメソッドは、非常に異なる歩行パターンの 2 つの系統を用いた線虫の運動の実験とモデル化された周波数スペクトルを比較します。線虫は、明確な顕微鏡画像は解析には必要ありませんので、水の列で泳ぐように、周波数スペクトルが変化に依存することを示した。このメソッドは、リアルタイム定量が可能、伝統的な顕微鏡で得られた画像/動画に相補的な情報を提供します。フラウンホーファー回折、遠視野の回折とも呼ばれますは、ライブの回折データ^1,2を取得するための基礎を提供します。回折パターンで任意の単一の時点で光の強度は、線虫の³の概要のすべてのポイントからの光を重ね合わせの結果です。その結果、光の強度を時間をかけて収集は線虫の移動についての情報を運ぶ。時間依存型回折信号の分析は従来のビデオ解析を補完する歩行に関与するすべての周波数の分析から対応する突然変異体の特徴的な運動を識別できます。この場合、「ローラー」の歩行と野生型線虫の特徴的な違いは、線虫の 2 つの異なる系統の周波数スペクトルを比較することによって確認しています。

いくつかの以前の特性は、周波数^2,4の水泳など回折信号の周波数解析を用いた確認されています。もっと重要なは、このメソッドは、データが収集されていると、コンピューターの画面上でリアルタイムに歩行を観察する伝統的な顕微鏡に相補的な方法として使用できます。異なる歩行パターンを持つワームの周波数スペクトルは、フーリエ変換回折信号の信号を考慮した定量化することができます。

この作品での回折のフーリエ ベースの学際的な性質には、生物学と物理学のフィールドが含まれます。アンダー ・ サンプリングによる回折は、結晶構造生物学⁵と他の分野を調査するため長い間使用されています。この実験では、しかし、^6、7をオーバー サンプリングが作成され遠視野の回折パターン レーザー光線で生物を中心します。オーバー サンプリングは通常レンズ少ないイメージング⁸元のオブジェクトのイメージを再構築フェーズ検索アルゴリズムと組み合わせて使用されます。位相回復による線虫の場合、散乱体が存在する場合を達成することは困難です。回折の時間署名は、ワームの動きの鍵域を評価するのに十分です。このメソッドは、計算負荷が少ないと運動を定量化する方法が光を提供します。この手法は、適応変異や行動を変える環境条件の分析のため容易にかもしれない。

プロトコル

1 です。 c. の elegans の成長とメインテナンス

1. 準備線虫の培養皿。
   1. ペトリ皿の寒天液を詰めて、にして、OP50 の エシェリヒア属大腸菌 の培養と種子ひずみ ^{9 , 10} を固め、おきます
   。
2. 大腸菌 パッチと新鮮な寒天培地充てんペトリ皿にいくつかの大人のワームを動かすことによって各プレート上の大人の線虫の開始人口を準備します。インキュベーターで 20 ° C で線虫の文化を維持します
   。 注: 線虫の系統は、線虫 ゲノム センターから入手できます。この研究、野生型、N2、ひずみ、OH7547 に (otls199 [猫 2::GFP + rgel-1 (F25B3.3):: した dsRed ローラー表現型を展示、rol-6(su1006)]) 株を利用した +
。
3. 将来の文化の伝達のワーム。 線虫 と未使用の生息地低温インキュベーターからペトリ皿を含む
   1. 削除ペトリ料理。解剖顕微鏡のステージの上に置きます
   。
   2. はブンゼン バーナーの光し、赤く点灯するまで炎に金属を配置することによってプラチナの線虫のピックを消毒します。部屋の温度に冷却するための選択を許可します。ピックを設定または汚染物質と接触ピックを聞かせしないでください
   。
   3. は、細菌の円の端にピックの先端をそっと触れます。この物質は粘着性と個々 の大人線虫を簡単にピッキングを行います
   。
   4. 線虫の成長媒体 (NGM) 寒天培地充てんペトリ プレートに最大 4 妊娠線虫を転送し、20 ° c. で孵化させなさいワームは 4 日間では、成熟卵が産むされます
   。
   5. 4 つの大人の線虫を移動した後、インキュベーターに残りの線虫を戻ります
   。

2。光セットアップ ( 図 1)

1. セキュア ヘリウム ネオン レーザー光のワークベンチの後ろの左隅付近、電源ソースに接続します
   。 注: レーザー ' s 梁がオーバー サンプリングのための要件を満たす必要があります。線虫 は長さ約 1 mm、回折パターンが見つけにくいようににレーザー光線で、線虫のインシデントが 5 mm を超える 2 mm より大きい直径したがって必要があります
。
2. レーザー ビームはサンプルを到達する前にフィルターを通過するようにヘリウム ネオン レーザーとサンプル間の中性密度フィルターを配置します
。 使用 2 つのフロント アルミ ステアリング
3. ミラーは、中性密度フィルター後最初のミラーを確保することで潜望鏡をビルドします。2 番目のミラーにレーザービームを操縦し、ミラー間キュベットを挿入する余地を与える最初のミラーの下約 10 cm を確保します。レーザービームがキュヴェットを垂直方向に通過されるようレーザー光とキュベット整列します
   。 注: 回折の有機体からフォト ダイオードまでの距離は、遠視野の回折を達成するためにそれ自身の有機物よりもはるかに大きい必要があります。この実験では、キュベットからフォト ダイオードまでの距離は 20 cm
。
4. ミラーに直面してそのセンサーと 2 番目のミラーの真向かいフォト ダイオードをセキュリティで保護します
   。 注: 線虫を含むキュベットは、化学のクランプを使用して 2 つのミラー間配置されます。セクション 4 と 5 を参照してください
。
5. は、スタンドに水で満たされたキュベットを配置します。スタンドの高さを調整します。レーザー光フォト ダイオードで直接ではなく、近くを目指したキュベットを通過できるように、高さとミラー 1 ・ ミラー 2 の角度を調整します
。
6. は、スタンド フォーム キュヴェットの水平面を確保するため、レベルを使用します。必要に応じて、さらにミラーを調整します
。
7. は、デジタル ・ オシロ スコープに付属 USB ケーブルを使用してデジタル ・ オシロ スコープにフォト ダイオードを接続します。デジタル ・ オシロ スコープを記録し、データを保存するために使用、コンピューターに接続します
。

3。オシロ スコープのセットアップ

1. コンピューターで、オシロ スコープのソフトウェアを使用してワームのスラッシング サイクルを十分に解決する少なくとも 8 Hz にサンプル レートを設定します
   。 注: サンプル レートされるべき 2 倍以上種の予想されるスラッシング周波数ナイキスト定理 ¹¹ が満たされるようにします
。

4。データ収集のワームとキュベットを準備

1. 4 アダルト線虫プレートに転送、新鮮な NGM ¹⁰ 寒天培地充てんペトリ薄い、平らにされたプラチナ ワイヤー ピック (セクション 1.3 を参照) を使用しています
。
2. だけその畝の両側のキュベットに触れるように注意しながら、パッケージから 1 つの使い捨てプラスチック キュベットを削除します
。
3. マイクロ ピペット ピペット キュヴェットが約 80% になるまでのキュヴェットに蒸留水に満ちて使用蒸留水します
   。 注:、蒸留水または M9 ¹⁰ などリン酸緩衝生理食塩水 (PBS) イオン バッファーのみに重要な線虫を処理するとき水道水には、微生物を殺す成分が含まれています
。
4. 切り裂くスコープ下に c. の elegans を含むペトリ皿を配置します
。
5. プラチナのピックを使用すると、シャーレから 1 つの成熟した 線虫 を削除し、線虫を取り除く必要がある場合、円でピックを移動、キュヴェットにピックを水没します
。 泡、キュヴェットの形成を防ぐために
6. 水でキュヴェットを入力は、それは少しキュヴェットの膨らみまで ' s トップ。キュベットを埋める ' 水、完全 s キャップはすぐにキュヴェットにキャップを置く
。
7. 以上、光の任意の小さい残りの水滴をきれいにする紙を洗浄こぼした場合があります水滴を除去する光洗浄布を使用します
。

5。回折パターン変化のリアルタイム データ集録

1. オンにヘリウム ネオン レーザーし、赤ビームを生成する周波数/色の設定を調整します。センサーを有効にします
   。 注意:632 で低エネルギービームを使用して nm、線虫 を避ける高周波 (青) の光 ¹²
。
2. は、キュベットでワームを探します。マツ材線虫病は約キュヴェットの部分の中心部まで優しくキュヴェットを傾けるその畝の両側のキュベットを保持します
   。 注: 振動またはキュベットを激しく傾斜キュヴェットの壁と衝突するワームが発生します。これは線虫を損傷することができます。
   1. レーザー内でワームを中心とした光学系でスタンドにキュベットの場所 ' s ビーム反射ミラー 1 ミラー 2。迷光を排除してください
   。
3. レーザ光線でワームを中心します。
   1. フォト ダイオードの位置と回折パターンの中心部最大一致しないように回折パターンのフォト ダイオードを配置します
   。
   2. は、フォト ダイオードの飽和を防ぐために中性密度フィルターを調整します。光の強度を調節する中立的な密度のフィルター ホイールを回転させます。
      1. 中性密度フィルター、フォト ダイオードからの出力電圧が増加するよう回転します
         。 注: デジタル フォト ダイオード用ソフトウェアを使用して、出力電圧が観察されます。フォト ダイオードは電圧が変化しない場合に飽和状態します。その場合は、平坦で最小の読書でせずに電圧が減少するまで中立的な密度のフィルターを回転します。電圧信号はフォト ダイオードの飽和を示すピークの測定値でない平らにすることを確認します。飽和が発生した場合、中立的な密度のフィルター ホイールを回転させることにより光の強度を減らす
      。
   3. 移動回折パターンは、ワームを監視しながら、オシロ スコープを制御するソフトウェアのスタート ボタンをクリックすると、フォト ダイオードを用いた表示、収集データ一度 ' s の動き。ワームがレーザー光線と、能の外に移動するまで測定を続けるションのパターンが消えて、通常かかる約 20 秒。 オシロ スコープ用ソフトウェアの停止ボタンをクリックして
      1. データ収集停止プロセス。各試行を保存 ' s データを .csv または .txt 形式
      。
4. 各々 の表現型の少なくとも 50 のデータ セットが収集されてまで手順 5.2 5.3 を繰り返します。トライアルあたり 8 から 10 の動物を使用します
。
5. キュヴェットは場合傷処分とワーム、および手順 4 を繰り返します。ワームが転送である場合、それを処分、繰り返し手順 4 同じキュベットを使用して前に蒸留水でキュヴェットをすすいでください
。
6. 手順を繰り返します 5、OH7547 を使用して " ローラー " ワームひずみを示すデータをラベルに注意しながらひずみ
。

6。データのフーリエ スペクトル

1. 離散フーリエ変換 ³ を行うことができるデータ解析プログラムに取得したデータをインポートします
。
2. ソフトウェアの高速フーリエ変換 (FFT) オプションを使用して各データ セット上の実行フーリエ変換します
。
3. N2 野生型の各振幅のワームの FFT の結果から周波数を平均します
。
4. 手順を繰り返します、OH7547 から Fft を使用して 6.3 " ローラー " ワーム
。

7。フーリエ スペクトルのモデリング

1. プログラム バイナリ モデル線虫の歩行 (補足資料に含まれているプログラムを参照してください).
   注: このモデルは概算でまずワームの動きの顕著な特徴を表示します。モデルは、成果が実際のワームと比較して洗練されたことができます。ワームの形状は、顕微鏡画像 ¹³ を使用して近似です。
   1. バイナリ モデルの少なくとも 2 つのワーム サイクル ( 図 2 a) 移動の連続したフレームを作成します。補足資料のビデオを見るC ワーム ビデオ (CWorm.avi) および W ワーム ビデオ (WWorm.avi) です
   。
2. 逐次回折パターンを作り出します。補足資料にビデオを参照してください。C ワーム回折ビデオ (CWormDiff.avi) および W ワーム ビデオ (WWormDiff.avi)。
   1. フーリエ変換各ワームのイメージのバイナリ フレームです。なるほどのパディングのワームを囲むフレームより回折像の解像度になります
      。 注: 各フーリエ変換されたフレームの絶対値は対応する回折パターン ( 図 2 b) に比例します
   。
   2. は、回折パターンの強度を対数目盛にマッピングして回折像のコントラストを調整します
      。 注: カメラと目の非線形スケールで機能する傾向があります。対数スケールは、どのように回折パターンは通常人間の目によって感知されるシミュレートできます
   。
3. モデル化された回折信号を抽出します。
   1. 回折パターンでフォト ダイオードの位置に対応する中心から外れた場所を選択します
   。
   2. は、フォト ダイオードのサイズをシミュレートするフォト ダイオードの位置を囲む隣接行列の要素を追加します。フォト ダイオードのサイズは通常モデルの回折パターンの 0.1% です
   。
   3. レコードとプロット回折の大きさの順序を示します。信号が物理的に合理的であることを確認してください (すなわち、定期的なスラッシングの場合、フォト ダイオードからの信号べき周期同様).
4. フーリエ 7.3 で得られた回折信号を変換し、実験データと結果を比較します
。
5. 系統のワームの繰り返しを比較しています
。

結果

図 1に示すように光の実験のセットアップは、微生物の研究、焦点面に縛られることがなくフォト ダイオードからのスラッシングの信号は、データが収集されるコンピューターの画面上でリアルタイムに観察できます。異常なパターンの詳細ビデオを分析することがなくすぐに目に見えることがされます。

パターンは図 2に示すようにモデル化されたシーケンシャル ワームの動きと対応する回折の例です。定性的モデル化された回折実験のパターン¹のように、シミュレーションが正常に線虫をモデルすること最初の徴候です。

ここで学んだの線虫の 2 つのタイプの一時的な回折署名のサンプルは図 3に示します。それ見ることができる質的各線虫が異なる速度振幅でバタバタしています。カーブフィッティングに以前文書¹で行われたいくつかの相違点の定量化できます。離散フーリエ変換は、ただし、埋め込み周波数に関する詳細を明らかにします。

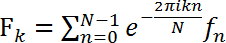、(1)

F_kはデジタルのフーリエ変換 (FT) f_nは離散時間と時間依存生回折信号n変数と離散周波数可変・ k ・ Nがどこの合計数データ ポイントです。平均デジタル フーリエ変換線虫その回折周波数スペクトル (図 4) の振幅によって識別することができます。野生型のスペクトルは、ローラーの動きスペクトルよりも低い周波数によって支配されます。

ローラー c. の elegansノート対野生型に近いモデル野生型ローラーはほぼ振動の C 形 (のような 1 つの側面を支持する傾向がある間波状 (W や S 形) 運動 (図 2 a) で徹底的に議論する傾向があります。図 5)。これは、異なるスペクトルのいくつかの解説をしています。W 振動は、2 つの向かい合う C 運動として考えることができますしながら、ローラは片側に C を形成主。このため、W モーションは明らかに C モーションよりもより多くの二次低周波複雑です。この結果は、計算のモデルで確認されています。W 形状が C 形 (図 6) よりもはるかに高い周波数の密度です。これは図 4ローラー周波数が中完全に離散的にクラスターより FFT で確認です。ローラは野生型歩行に一時的に戻すことができますので、ローラーの統計情報が偏っています。

ローラー タイプの平滑化スペクトル線虫~1.5 Hz でスイミング野生型線虫展示マルチ モーダル スペクトル (~1.0 Hz と 1.75 Hz 含むピーク)、ブロードなピークを示します。フォト ダイオード (PD) の有限サイズはいくつかの行列要素上で広がっています。個々 の行列要素または回折パターン上のポイントは強度が違うので建設的かつ破壊的な干渉が異なります。とはいえ、強度が変化する周波数は図 7に見られるようにすべての行列要素の同じであります。時間微分方程式 1 を考慮した位相マトリックスではなく元のオブジェクトの変動のみ周波数変動に依存しないことを見ることができます。

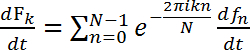、(2)

いくつかの行列要素を PD として、ピーク位置の一貫した周波数プロファイルに平均します。いくつかのバリエーションが期待できるし、ワームの向きについての手がかりを与えることができます。ワーム変更の歩行として度数分布が変わります。現在のモデルだけ相対的なピークの高さよりもむしろピーク位置の評価ができるシンプルなモデルです。異なる歩行パターンは、異なるピーク位置を平均します。

図 1。実験のセットアップ。低消費電力のレーザー ビーム通過中性密度フィルターはミラー M2、およびフォト ダイオードへの旅の上にワームを含むキュベットからダウン ミラー M1 に反映されます。この図の拡大版を表示するのにはここをクリックしてください。

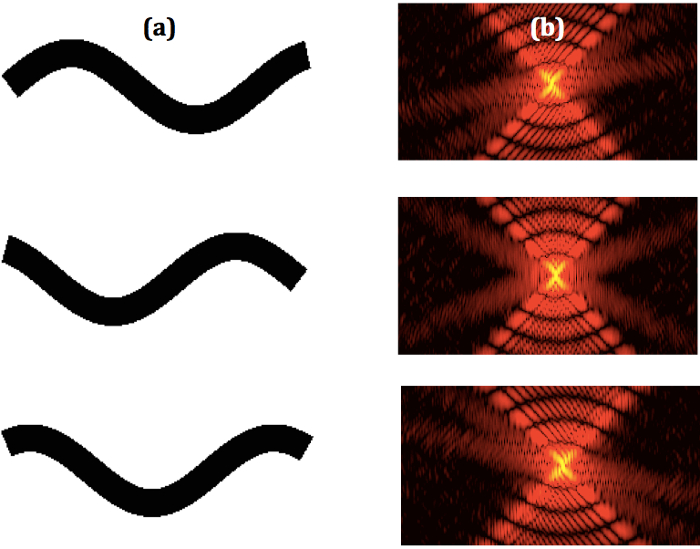
図 2。シーケンシャル ワーム形状と対応する回折パターン。(、) 一部はモデルの W 形状線虫、(b) 対応する逐次回折パターンの逐次バイナリ イメージを選択しています。この図の拡大版を表示するのにはここをクリックしてください。

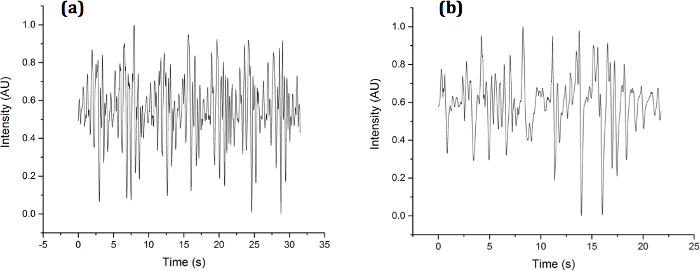
図 3。実験試料回折署名します。回折署名収集 (、) OH7547「ローラー」と (b) N2 野生型線虫回折パターン.に単一のフォト ダイオードを使用してこの図の拡大版を表示するのにはここをクリックしてください。

図 4。実験的平均ローラーと野生型フラウンホーファー回折シリーズのパワー スペクトル。フォト ダイオードと時系列の平均のフーリエ変換で周波数を提示スペクトル表示が記録されます。ガウス フィルター標準偏差 0.075 Hz、3 標準偏差で切り捨て平滑化に使用されます。~1.5 Hz (~1.0 と 1 のピークを含むマルチ モーダル平滑野生型スペクトルと比較して平滑ローラー スペクトルの広いスペクトル ピークを注意してください。.75 Hz)。この図の拡大版を表示するのにはここをクリックしてください。

図 5。回折形成図。回折パターンは無限小のストレート ラインを (左) として各線分の思考見なすことができます。C 型のマツ材線虫病によって生成される遠視野の回折パターンの構築を示します (右) にこれらの行を重ね合わせます。この図の拡大版を表示するのにはここをクリックしてください。

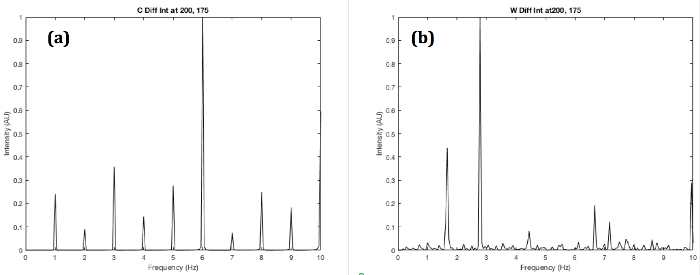
図 6。ローラーと野生型フラウンホーファー回折シリーズのパワー スペクトルをシミュレートします。200 (垂直) と 175 (水平) (、) C 形と (b) W 形ワーム、フォト ダイオードを用いた中心行列要素と。W シェープより複雑な運動による周波数のより高い密度を示しています。この図の拡大版を表示するのにはここをクリックしてください。

図 7。ローラーと異なるフォト ダイオードの場所で野生型フラウンホーファー回折シリーズのパワー スペクトルをシミュレートします。(、) W 形状のワームやフォト ダイオードのさまざまな場所をシミュレートするさまざまな場所で 1 つの行列要素の (b) C 形ワーム。ピークの高さによって異なるさまざまな位置がある;ただし、ピーク位置は、特定の図形と同じままです。この図の拡大版を表示するのにはここをクリックしてください。

ディスカッション

人工的に低い周波数平均が結果になりますので非アクティブ データの伸張を含む結果が歪曲されます。フォト ダイオードの飽和は、平らな山または raw データで「切断」のピークによって認識することができます。ピーク強度によって各 raw データ セットを分割は、レーザー強度変動の会計処理に役立ちます。

ピーク周波数の全体的な指標は、スラッシング周波数;しかし、複雑な動きは回折パターンのビート周波数の干渉を引き起こす、慎重に検討する必要があります。

このメソッドは、他の線虫の移動を調査する使用することができます。環境は、別のメディアに変更できます。波長だけでなく変更できます。電磁スペクトルの目に見える範囲での作業は、最も簡単なと最も安全なです。

洗練されたモデルは、将来的により現実的に回折スペクトルをシミュレートします。将来のモデルは周波数の場所が相対的なピークの高さには影響しません、向きを変えることができるワームを含めることができます。現実的なモデルは、スラッシングの周波数は、実験データのようにピークを広げることの確率分布になります。周波数拡散をスラッシング周波数のばらつきを占めます。

現在のワーム形状は、現在のモデルよりもよりテーパーにする必要があります頭と尾の地域特に原油です。興味深い異なる突然変異における歩行の複雑さについての手がかりを与えることができるので、信号の時系列データの詳細な分析を実施する場合があります。

この手法が同時に複数の線虫を特徴付ける進出の実用性を考慮した価値があります。このメソッドは、従来の顕微鏡を使用して既存のメソッドに相補的な方法として理解すべき。このメソッドには、焦点面からワームを移動ことがありますように、データ集録時に顕微鏡を要求しないという利点があります。平均周波数スペクトルはワームの動きに明らかな違いを示すし、流行している周波数のピークによって定量することができますワーム運動を定量化する手法であります。回折署名のデータ分析が発展で、うまくいけば複数の突然変異体および個人の自動認識プロセスに 。

資料

Name	Company	Catalog Number	Comments
Tunable Helium-Neon laser	Research Electro-Optics	30602	Four wavelengths can be selected between 543 nm and 633 nm.
2 Front Surface Aluminum Mirrors	Thorlabs	PF10-03-F01
Photodiode: SI Amplified Detector	Thorlabs	PDA 100A
Quartz Cuvette	Starna Cells	21/G/5	Plastic cells may be used as well.
MatLab (Software)	MathWorks	R2016b (9.1.0.441655)	Use the fft command to simulate diffraction
Excel	Microsoft	14.7.1	Used for data analysis of Figure 4
Caenorhabditis elegans Roller	University of Minnesota Caenorhabditis elegans Center (CGC)	Strain: OH7547 Genotype: otIs199.	https://cbs.umn.edu/cgc/home
Caenorhabditis elegans Wild Type	University of Minnesota Caenorhabditis elegans Center (CGC)	Strain:N2 Genotype: C. elegans wild isolate	https://cbs.umn.edu/cgc/home