28.12 : Thomson's e/m Experiment
In a beam of charged particles created by a heated cathode, the particles move at different speeds. However, many applications need a beam with uniform particle speeds. An arrangement known as a velocity selector uses electric and magnetic fields to pick particles with a particular speed from the beam.
A particle with charge q, speed v, and mass m enters an area from the top, where the magnetic and electric fields are perpendicular both to the particle's motion and to one another. The magnetic field is into the plane of the paper, while the electric field E is to the left. If the charge q is positive, the magnetic force is towards the right with magnitude qvB, and the electric force is towards the left with magnitude qE. The two forces are equal in strength for the given field strengths E and B for a specific value of v, for which the total force is zero, given by
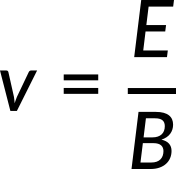
J. J. Thomson (1856–1940) used this concept to determine the electron's charge-to-mass ratio in one of the classic physics experiments at the end of the 19th century. A voltage difference between the two anodes and cathodes in a highly evacuated glass container accelerates and shapes a beam of hot cathode electrons. The accelerating potential V determines the electrons' velocity v. The lost electric potential energy equals the acquired kinetic energy.
Only the electrons with a speed equal to E/Bcan pass straight through the crossed electric and magnetic fields and strike the fluorescent screen that glows at the point of impact.
The electron's charge-to-mass ratio is calculated to be
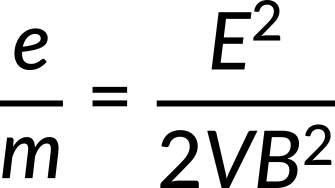
Its value is determined as follows:
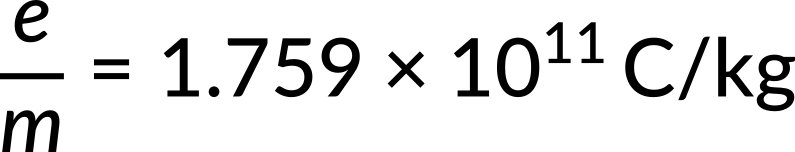
The fact that Thomson only discovered one value for this number was an essential feature of his measurements. The cathode material, the remaining gas in the tube, or any other aspect of the experiment had no bearing on it. This independence demonstrated that the beam's constituent particles, now known as electrons, are a component of all matter. As a result, Thomson is credited with discovering the electron as the first elementary and truly fundamental particle.
The American scientist Robert Millikan could precisely measure the electron's charge 15 years after Thomson's investigations. This number and the charge-to-mass ratio made it possible to calculate the electron's mass. Currently, the most exact value that is obtainable is

Z rozdziału 28:

Now Playing
28.12 : Thomson's e/m Experiment
Magnetic Forces and Fields
3.3K Wyświetleń

28.1 : Magnetyzm
Magnetic Forces and Fields
6.3K Wyświetleń

28.2 : Pola magnetyczne
Magnetic Forces and Fields
5.9K Wyświetleń

28.3 : Linie pola magnetycznego
Magnetic Forces and Fields
4.0K Wyświetleń

28.4 : Strumień magnetyczny
Magnetic Forces and Fields
3.5K Wyświetleń

28.5 : Ruch naładowanej cząstki w polu magnetycznym
Magnetic Forces and Fields
4.6K Wyświetleń

28.6 : Siła magnetyczna
Magnetic Forces and Fields
907 Wyświetleń

28.7 : Siła magnetyczna działająca na przewodnik przewodzący prąd
Magnetic Forces and Fields
4.0K Wyświetleń

28.8 : Siła magnetyczna działająca na przewody przewodzące prąd: przykład
Magnetic Forces and Fields
1.4K Wyświetleń

28.9 : Wymuś pętlę prądową w polu magnetycznym
Magnetic Forces and Fields
3.2K Wyświetleń

28.10 : Moment obrotowy w pętli prądowej w polu magnetycznym
Magnetic Forces and Fields
3.8K Wyświetleń

28.11 : Efekt Halla
Magnetic Forces and Fields
2.2K Wyświetleń
Copyright © 2025 MyJoVE Corporation. Wszelkie prawa zastrzeżone