Aby wyświetlić tę treść, wymagana jest subskrypcja JoVE. Zaloguj się lub rozpocznij bezpłatny okres próbny.
Method Article
Uncoupling Coriolis Force and Rotating Buoyancy Effects on Full-Field Heat Transfer Properties of a Rotating Channel
W tym Artykule
Podsumowanie
Here, we present an experimental method for decoupling the interdependent Coriolis-force and rotating-buoyancy effects on full-field heat transfer distributions of a rotating channel.
Streszczenie
An experimental method for exploring the heat transfer characteristics of an axially rotating channel is proposed. The governing flow parameters that characterize the transport phenomena in a rotating channel are identified via the parametric analysis of the momentum and energy equations referring to a rotating frame of reference. Based on these dimensionless flow equations, an experimental strategy that links the design of the test module, the experimental program and the data analysis is formulated with the attempt to reveal the isolated Coriolis-force and buoyancy effects on heat transfer performances. The effects of Coriolis force and rotating buoyancy are illustrated using the selective results measured from rotating channels with various geometries. While the Coriolis-force and rotating-buoyancy impacts share several common features among the various rotating channels, the unique heat transfer signatures are found in association with the flow direction, the channel shape and the arrangement of heat transfer enhancement devices. Regardless of the flow configurations of the rotating channels, the presented experimental method enables the development of physically consistent heat transfer correlations that permit the evaluation of isolated and interdependent Coriolis-force and rotating-buoyancy effects on the heat transfer properties of rotating channels.
Wprowadzenie
While thermodynamic laws dictate the improved specific power and thermal efficiency of a gas turbine engine by elevating the turbine entry temperature, several hot engine components, such as turbine blades, are prone to thermal damage. Internal cooling of a gas turbine rotor blade permits a turbine entry temperature in excess of the temperature limits of the creep resistance of the blade material. However, the configurations of the internal cooling channels must comply with the blade profile. In particular, the coolant rotates within the rotor blade. With such harsh thermal conditions for a running gas turbine rotor blade, an effective blade cooling scheme is crucial to ensure the structure's integrity. Thus, the local heat transfer properties for a rotating channel are important for the efficient usage of the limited coolant flow available. The acquisition of useful heat transfer data that are applicable to the design of the internal coolant passages at realistic engine conditions is of primary importance when an experimental method is developed for measuring the heat transfer properties of a simulated cooling passage inside a gas turbine rotor blade.
Rotation at a speed above 10,000 rpm considerably alters the cooling performance of a rotating channel inside a gas turbine rotor blade. The identification of engine conditions for such a rotating channel is permissible using the similarity law. With rotation, the dimensionless groups that control the transport phenomena inside a radially rotating channel can be revealed by deriving the flow equations relative to a rotating frame of reference. Morris1 has derived the momentum conservation equation of flow relative to a rotating frame of reference as:
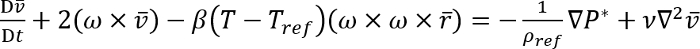 (1)
(1)
In equation (1), the local fluid velocity, v̄, with the position vector, r̄, relative to a frame of reference rotating at the angular velocity, ω, is affected by the Coriolis acceleration in terms of 2(ω×v̄), the decoupled centripetal buoyancy force, β(T-Tref)(ω×ω×r̄), the driven piezo-metric pressure gradient,  , and the fluid dynamic viscosity, ν. The referenced fluid density, ρref, is referred to a pre-defined fluid reference temperature Tref, which is typical of the local fluid bulk temperature for experiments. If the irreversible conversion of mechanical energy into thermal energy is negligible, the energy conservation equation is reduced to:
, and the fluid dynamic viscosity, ν. The referenced fluid density, ρref, is referred to a pre-defined fluid reference temperature Tref, which is typical of the local fluid bulk temperature for experiments. If the irreversible conversion of mechanical energy into thermal energy is negligible, the energy conservation equation is reduced to:
 (2)
(2)
The first term of equation (2) is obtained by treating the specific enthalpy to be directly related to the local fluid temperature, T, via the constant specific heat, Cp. As the perturbation of fluid density caused by the variation of fluid temperature in a heated rotating channel provides considerable influence on the motion of fluids when it links with the centripetal acceleration in equation (1), the fluid velocity and temperature fields in an axially rotating channel are coupled. Also, both Coriolis and centripetal accelerations vary simultaneously as the rotating speed is adjusted. Thus, the effects of Coriolis force and rotating buoyancy on the fields of fluid velocity and temperature are naturally coupled.
Equations (1) and (2) in the dimensionless forms disclose the flow parameters that govern the heat convection in a rotating channel. With a basically uniform heat flux imposed on a rotating channel, the local fluid bulk temperature, Tb, increases linearly in the streamwise direction, s, from the reference inlet level, Tref. The local fluid bulk temperature is determined as Tref + τs, where τ is the gradient of the fluid bulk temperature in the direction of flow. Substitutions of the following dimensionless parameters of:
 (3)
(3)
 (4)
(4)
 (5)
(5)
 (6)
(6)
 (7)
(7)
into equations (1) and (2), where Vmean, N and d respectively stand for the mean flow through velocity, rotating velocity and channel hydraulic diameter, the dimensionless flow momentum and energy equations are derived as equations (8) and (9) respectively.
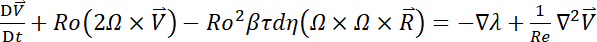 (8)
(8)
 (9)
(9)
Evidently, η in equation (9) is a function of Re, Ro, and Bu = Ro2βτdR, which are respectively referred to as Reynolds, rotation and buoyancy numbers. The Rossby number that quantifies the ratio between inertial and Coriolis forces is equivalent to the inverse rotation number in equation (8).
When Tb is calculated as Tref + τs in a rotating channel subject to a uniform heat flux, the τ value can be alternatively evaluated as Qf/(mCpL) in which Qf, m and L are the convective heating power, coolant mass flow rate and channel length, respectively. Thus, the dimensionless local fluid bulk temperature, ηb, is equal to s/d and the dimensionless temperature at channel wall, ηw, yields [(Tw-Tb)/Qf][mCp][L/d]+s/d. With the convective heat transfer rate defined as Qf/(Tw-Tb), the dimensionless wall-to-fluid temperature difference, ηw-ηb, is convertible into the local Nusselt number via equation (10) in which ζ is the dimensionless shape function of heating area and channel sectional area.
 (10)
(10)
With a set of predefined geometries and the hydrodynamic and thermal boundary conditions, the dimensionless groups controlling the local Nusselt number of a rotating channel are identified as:
 (11)
(11)
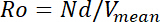 (12)
(12)
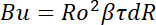 (13)
(13)
With experimental tests, the adjustment of rotating speed, N, for varying Ro to generate the heat transfer data at different strengths of Coriolis forces inevitably changes the centripetal acceleration, and thus, the relative strength of rotating buoyancy. Moreover, a set of heat transfer data collected from a rotating channel is always subject to a finite degree of rotating buoyancy effect. To disclose the individual effects of Coriolis-force and buoyancy on the heat transfer performance of a rotating channel requires the uncoupling of the Ro and Bu effects on Nu properties through the post data processing procedure that is inclusive in the present experimental method.
The engine and laboratory flow conditions for a rotating channel inside a gas turbine rotor blade can be specified by the ranges of Re, Ro and Bu. The typical engine conditions for the coolant flow through a gas turbine rotor blade, as well as the construction and commissioning of the rotating test facility that allowed experiments to be performed near the actual engine conditions was reported by Morris2. Based on the realistic engine conditions summarized by Morris2, Figure 1 constructs the realistic operating conditions in terms of Re, Ro and Bu ranges for a rotating coolant channel in a gas turbine rotor blade. In Figure 1, the indication of an engine's worst condition is referred to as the engine running condition at the highest rotor speed and the highest density ratio. In Figure 1, the lower limit and worst engine operating conditions respectively emerge at the lowest and highest engine speeds. It is extremely difficult to measure the full-field Nu distribution of a rotating channel running at a real engine speed between 5000 and 20,000 rpm. However, based on the similarity law, laboratory-scale tests have been conducted at reduced rotating speeds but with several attempts to provide a full coverage of the real-engine Re, Ro and Bu ranges. As an innovative experimental method, the NASA HOST program3,4,5,6 adopted the high-pressure tests for increasing the fluid densities at the predefined Re in order to extend the Ro range by reducing the mean fluid velocity. In this regard, the specific relationships between Re, Ro and Bu for an ideal gas with a gas constant, Rc, and viscosity, μ, are related as:
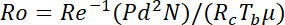 (14)
(14)
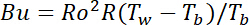 (15)
(15)
To bring the laboratory conditions into the nominal correspondence with engine conditions seen in Figure 1, the rotating speed, N, coolant pressure, P, channel hydraulic diameter, d, rotating radius, R, and wall-to-fluid temperature difference, Tw-Tb, need to be controlled for matching the realistic Re, Ro and Bu ranges. Clearly, one of the most effective approaches to extend the Ro range is to increase channel hydraulic diameter, as Ro is proportional to d2. As the laboratory heat transfer test at realistic N is extremely difficult, the coolant pressure, P, is technically easier to be raised for extending Ro range; even if Ro is only proportional to P. Based on this theoretical background, the design philosophy of the present experimental method is to increase Ro by pressurizing the rotating test channel using the maximum channel hydraulic diameter allowed to fit into the rotating rig. Having increased the Ro range, the range of Bu is accordingly extended as Bu is proportional to Ro2. In Figure 1, the laboratory test conditions adopted to generate the heat transfer data of rotating channels are also included3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29. As indicated in Figure 1, the coverage of realistic engine conditions by the available heat transfer data is still limited, especially for the required Bu range. The open and the colored solid symbols depicted in Figure 1 are the pointed and full-field heat transfer experiments, respectively. As collected in Figure 1, most of the heat transfer data with cooling applications to gas turbine rotor blades1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,20,21,22,23,24,25,26 are point measurements using the thermocouple method. The wall conduction effects on measuring the wall conductive heat flux and the temperatures at fluid-wall interfaces undermine the quality of heat transfer data converted from the thermocouple measurements. Also, the heat transfer measurements1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,20,21,22,23,24,25,26 using the thermocouple method cannot detect the two-dimensional heat transfer variations over a rotating surface. With the present experimental method29,30,31,32, the detection of full-field Nusselt number distributions over the rotating channel wall is permissible. The minimization of wall conduction effect using 0.1 mm thick stainless-steel foils with Biot numbers >>1 to generate the heating power by the present experimental method permits the one-dimensional heat conduction from the heating foil to the coolant flow. In particular, the acquisition of full-field heat transfer data involving both Ro and Bu effects is not permissible using the transient liquid crystal technique and the thermocouple method. With the current steady-state liquid crystal thermography method19, the detectable temperature range of 35-55 °C disables the generation of heat transfer data with realistic density ratios.
Using the flow parameters governing the heat convection in a rotating channel to demonstrate that the full coverage of realistic engine conditions seen in Figure 1 has not yet been achieved, so the need for acquiring the full-field heat transfer data at realistic engine conditions has been continuously urged. The present experimental method enables the generation of full-field heat transfer with both Coriolis-force and rotating-buoyancy effects detected. The protocols are aimed at assisting the investigators to devise an experimental strategy relevant to the realistic full-field heat transfer measurement of a rotating channel. Along with the method of parametric analysis that is unique to the present experimental method, the generation of heat transfer correlation for assessing the isolated and interdependent Ro and Bu effects on Nu is permitted.
The article illustrates an experimental method aimed at generating the two-dimensional heat transfer data of a rotating channel with flow conditions similar to the realistic gas turbine engine conditions but operating at much lower rotating speeds in the laboratories. The method developed to select the rotating speed, the hydraulic diameter of test channel and the range of wall-to-fluid temperature differences for acquiring the heat transfer data at realistic engine conditions is illustrated in the introduction. The calibration tests for the infrared thermography system, the heat loss calibration tests and the operation of the rotating heat transfer test rig are shown. The factors causing the significant uncertainties for heat transfer measurements and the procedures for decoupling the Coriolis-force and buoyancy effects on the heat transfer properties of a rotating channel are described in the article with the selective results to demonstrate the present experimental method.
Protokół
NOTE: The details of rotating test facilities, data acquisition, data processing and the heat transfer test module emulating an internal cooling channel of a gas turbine rotor blade are in our previous works29,30,31,32.
1. Preparation of Heat Transfer Tests
- Formulate the experimental conditions in terms of Re, Ro and Bu from the targeted operation conditions of a gas turbine rotor blade.
- Determine the N, P, d, R, and Tw - Tb needed for acquiring the tested Re, Ro and Bu using equations (14) and (15).
- Re-define the targeting Re, Ro and Bu if N, P, d, R, and Tw - Tb exceeds the limit of the experimental facilities.
- Design and construct the scaled heat transfer test module emulating a practical internal coolant channel in a gas turbine rotor blade2.
2. Determination of Thermal Emissivity Coefficient for Infrared Thermography System
- Install the calibrated thermocouple on the back side of the scanned stainless-steel heating foil.
- Spray a thin layer of black paint on the stainless-steel heating foil scanned by the infrared camera.
- Create symmetrical flow fields on two sides of the stainless-steel heating foil by placing a vertical thin stainless-steel foil in a space with the free convective flows over the two sides of the vertical heating foil.
- Feed electrical heating power through the heating foil and measure temperatures simultaneously by thermocouple and infrared thermography system from the computer display at steady state.
- Repeat step 2.4 at least four times using elevated heater powers. Ensure that the wall temperatures corresponding to the heater powers used by steps 2.3 and 2.4 cover the Tw range determined by step 1.2.
- Calculate the Tw values scanned by the infrared thermography system using a number of selective thermal emissivity coefficients for the program that converts the infrared signals into temperature data.
- Compare the Tw data measured by the calibrated thermocouple and the infrared thermography system at the location corresponding to the thermocouple spot with the standard deviations evaluated.
- Select the thermal emissivity coefficient with the minimum standard deviation determined by step 2.7.
- Determine the maximum precision error for the infrared thermography system using the thermal emissivity coefficient determined by step 2.8.
3. Dynamic Balance of Rotating Rig
- Install the heat transfer test module, the infrared camera, the enveloping frame and all accessories on the rotating rig.
- Adjust the counterbalancing weight gradually until the running condition of the rotating rig satisfies the vibrational limitation for the infrared thermographic measurements to exhibit the stable thermal image on the computer display.
4. Evaluation of Heat Loss Coefficients
- Fill the coolant channel of the heat transfer test module with thermal insulation material.
- Install the filled test module on the rotating test rig by fitting the test module on the rotating platform and connecting the heater power supply and all the instrumental cables.
- Activate the data acquisition system to scan the temporal Tw variation at a heating power until the steady state condition is satisfied. Ensure that the temporal Tw variations during several successive scans are less than +0.3 K at each steady state condition.
- Record the heater power, steady-state Tw data and the corresponding ambient temperature, T∞.
- Repeat steps 4.3 and 4.4 at least five times using different heating powers at a fixed rotating speed.
- Repeat steps 4.2 - 4.4 with at least five rotating speeds. Ensure that the test range of the rotating speed covers all the N values determined by step 1.2.
- Repeat steps 4.3 - 4.6 with a reversed rotating direction.
- Construct the plots of heat loss flux against wall-to-ambient temperature difference at each rotating speed.
- Correlate the heat loss coefficients as the functions of wall-to-ambient temperature difference, rotating speed and direction of rotation.
- Incorporate the heat loss correlation into the post data process program for Nu accountancy.
5. Baseline Heat Transfer Tests
- Perform heat transfer tests at the targeting Reynolds numbers at zero rotating speed (Ro = N = 0) by feeding coolant flows and heater powers to the test module. Ensure the supplied coolant mass flow rate is constantly adjusted in order to control Reynolds number at the flow entry plane at the targeting value.
- Record all the relevant raw data, including the steady state wall temperatures, fluid temperatures, heater powers, flow pressures and ambient pressures and temperatures, for subsequent data processing.
- Evaluate the local and area-averaged Nusselt numbers (Nu0) over the scanned static channel walls.
6. Rotating Heat Transfer Tests
- Install the on-line monitoring program to monitor the test conditions at the targeting Re and Ro.
- Feed the measured coolant mass flow rate, airflow pressure, rotating speed and fluid temperature at channel entrance into the monitoring program to calculate the instant Re and Ro.
- Record all the relevant raw data, such as rotating speed, heater power, airflow and ambient pressures, as well as the wall and fluid temperatures for subsequent data processing after the pre-defined steady-state condition is satisfied.
- Repeat steps 6.2 and 6.3 with at least four ascending or descending heater powers at a set of fixed Re and Ro. Ensure that the test Re and Ro fall within ±1% differences from the targeting values by adjusting the rotating speed or the coolant mass flow rate or both.
- Ensure that the heat transfer tests at each set of fixed Re and Ro with different heater powers are continuously performed as the development of buoyancy induced flows is associated with the "history" of the flow development.
- Repeat steps 6.4 and 6.5 with four or five targeting Reynolds numbers (Re) at a fixed rotation number (Ro). Ensure the rotating speed is appropriately adjusted at each test Re to control both Re and Ro at the targeting values within ±1% differences.
- Repeat step 6.6 using four or five targeting rotation numbers (Ro).
- Repeat steps 6.2 to 6.7 with reversed rotating direction.
- Evaluate the local and area-averaged Nusselt numbers (Nu) over the scanned rotating channel walls using a post data processing program.
7. Parametric Analysis
- Correlate the area-averaged Nusselt numbers (Nu0) collected from the static channel into the functions of Reynolds number.
- Evaluate the full-field local Nu/Nu0 ratios at each fixed Re and Ro tested with the area-averaged Nu/Nu0 ratios calculated.
- Verify the applicability of isolation Re effect by plotting the local and area-averaged Nu/Nu0 ratios obtained with different Re but at identical Ro.
- Disclose the isolated impacts of rotating buoyancy on heat transfer properties of the rotating test channel by plotting the area-averaged Nu/Nu0 ratios collected at the same Ro with different Re against Bu or density ratio (Δρ/ρ). Ensure the preferable selection of Bu or Δρ/ρ to construct this type of plot for obtaining the consistent data trend with a simple functional structure for heat transfer correlation.
- Extrapolate each Nu/Nu0 data trend collected at a fixed Ro but different Re into the limiting condition of Bu→0 or Δρ/ρ→0.
- Collect all the extrapolated Nu/Nu0 results with Bu→0 or Δρ/ρ→0 at all the tested Ro.
- Plot the extrapolated Nu/Nu0 results with vanished buoyancy interaction against Ro to disclose the uncoupled Coriolis force effects on the heat transfer properties.
- Correlate the test results collected by steps 7.4 and 7.7 into the functions of Ro and Bu.
Wyniki
Realistic operating conditions for the internal coolant flows inside a rotating gas turbine blade in terms of Re, Ro and Bu are compared with the emulated laboratory conditions in Figure 1. The data points fall in the realistic engine conditions using the present experimental method summarized in the protocols11,14,17,20,
Dyskusje
While the endwall temperatures of a rotating channel are detected by an infrared thermography system, the fluid temperatures are measured by thermocouples. As the alternative magnetic field of an AC motor that drives a rotating rig induces electrical potential to interfere the thermocouple measurements, the DC motor must be adopted to drive a rotating test rig.
The fluid temperature distribution over the exit plane of a heated channel is not uniform. At least five thermocouples on the existing...
Ujawnienia
The authors have nothing to disclose.
Podziękowania
The present research work was financially sponsored by the Ministry of Science and Technology of Taiwan under the grant NSC 94-2611-E-022-001, NSC 95-2221-E-022-018, NSC 96-2221-E-022-015MY3 and NSC 97-2221-E-022-013-MY3.
Materiały
| Name | Company | Catalog Number | Comments |
| Rotating test rig | In-house made | Design by this research group | |
| Heat transfer test module | In-house made | Design by this research group | |
| Mass flow meter | Eldride Product, Inc. | 3100301-01-01 359-1007 | |
| Infrared thermography system | NEC P384A-8 | 3100401-04 3127A-4 | |
| Instrumentation slip ring | Michigan Scientific SR36M | 3100506-62 3553-372 |
Odniesienia
- Morris, W. D. . Heat transfer and fluid flow in rotating coolant channels. , ISBN 0471101214 (1981).
- Morris, W. D. A rotating facility to study heat transfer in the cooling passage of turbine rotor blades. Journal of Power and Energy. 210 (1), 55-63 (1996).
- Wagner, J. H., Johnson, B. V., Graziani, R. A., Yeh, F. C. Heat transfer in rotating passages with smooth walls and radially outward flow. ASME Journal of Turbomachinery. 113 (1), 42-51 (1991).
- Wagner, J. H., Johnson, B. V., Kopper, F. C. Heat transfer in rotating serpentine passages with smooth walls. ASME Journal of Turbomachinery. 113 (3), 321-330 (1991).
- Wagner, J. H., Johnson, B. V., Steuber, G. D., Yeh, F. C. Heat transfer in rotating serpentine passages with trips normal to the flow. ASME Journal of Turbomachinery. 114 (4), 847-857 (1992).
- Johnson, B. V., Wagner, J. H., Steuber, G. D., Yeh, F. C. Heat transfer in rotating serpentine passages with selected model orientations for smooth or skewed trip walls. ASME Journal of Turbomachinery. 116 (4), 738-744 (1992).
- Hwang, G. J., Tzeng, S. C., Mao, C. P., Soong, C. Y. Heat transfer in a radially rotating four-pass serpentine channel with staggered half-v rib turbulators. ASME Journal of Heat Transfer. 123 (1), 39-50 (2001).
- Azad, G. S., Uddin, M. J., Han, J. C., Moon, H. K., Glezer, B. Heat transfer in a two-pass rectangular rotating channel with 45-deg angled rib turbulators. ASME Journal of Turbomachinery. 124 (2), 251-259 (2002).
- Griffith, T. S., Al-Hadhrami, L., Han, J. C. Heat transfer in rotating rectangular cooling channels (AR=4) with angled ribs. ASME Journal of Heat Transfer. 124 (4), 617-625 (2002).
- Al-Hadhrami, L., Griffith, T. S., Han, J. C. Heat transfer in two-pass rotating rectangular channels (AR=2) with five different orientations of 45 deg V-shaped rib turbulators. ASME Journal of Heat Transfer. 125 (2), 232-242 (2003).
- Chang, S. W., Liou, T. M., Hung, J. H., Yeh, W. H. Heat transfer in a radially rotating square-sectioned duct with two opposite walls roughened by 45 deg staggered ribs at high rotation numbers. ASME Journal of Heat Transfer. 129 (2), 188-199 (2007).
- Zhou, F., Lagrone, J., Acharya, S. Internal cooling in 4:1 AR passages at high rotation numbers. ASME Journal of Heat Transfer. 129 (12), 1666-1675 (2007).
- Liu, Y. H., Huh, M., Han, J. C., Chopra, S. Heat transfer in a two-pass rectangular channel (AR=1:4) under high rotation numbers. ASME Journal of Heat Transfer. 130 (8), (2008).
- Chang, S. W., Liou, T. M., Chiou, S. F., Chang, S. F. Heat transfer in high-speed rotating trapezoidal duct with rib-roughened surfaces and air bleeds from the wall on the apical side. ASME Journal of Heat Transfer. 130 (6), (2008).
- Wright, L. M., Liu, Y. H., Han, J. C., Chopra, S. Heat transfer in trailing edge, wedge-shaped cooling channels under high rotation numbers. ASME Journal of Heat Transfer. 130 (7), 1-11 (2008).
- Liou, T. M., Chen, M. Y., Tsai, M. H. Fluid flow and heat transfer in a rotating two-pass square duct with in-line 90-deg ribs. ASME Journal of Turbomachinery. 124 (2), 260-268 (2002).
- Chang, S. W., Liou, T. M., Yang, T. L., Hong, G. F. Heat transfer in radially rotating pin-fin channel at high rotation numbers. ASME Journal of Turbomachinery. 132 (2), (2010).
- Rallabandi, A., Lei, J., Han, J. C., Azad, S., Lee, C. P. Heat transfer measurements in rotating blade-shape serpentine coolant passage with ribbed walls at high Reynolds numbers. ASME Journal of Turbomachinery. 136 (9), (2014).
- Mayo, I., Arts, T., Ahmed, E. H., Parres, B. Two-dimensional heat transfer distribution of a rotating ribbed channel at different Reynolds numbers. ASME Journal of Turbomachinery. 137 (3), (2015).
- Chang, S. W., Yang, T. L., Liou, T. M., Fang, H. G. Heat transfer in rotating scale-roughened trapezoidal duct at high rotation numbers. Applied Thermal Engineering. 29 (8), 1682-1693 (2009).
- Liou, T. M., Chang, S. W., Chen, J. S., Yang, T. L., Lan, Y. A. Influence of channel aspect ratio on heat transfer in rotating rectangular ducts with skewed ribs at high rotation numbers. International Journal of Heat Mass Transfer. 52 (23), 5309-5322 (2009).
- Huh, M., Liu, Y. H., Han, J. C. Effect of rib height on heat transfer in a two pass rectangular channel (AR = 1:4) with a sharp entrance at high rotation numbers. International Journal of Heat Mass Transfer. 52 (19), 4635-4649 (2009).
- Xu, G., Li, Y., Deng, H. Effect of rib spacing on heat transfer and friction in a rotating two-pass square channel with asymmetrical 90-deg rib turbulators. Applied Thermal Engineering. 80 (5), 386-395 (2015).
- Tao, Z., Yang, M., Deng, H., Li, H., Tian, S. Heat transfer study in a rotating ribbed two-pass channel with engine-similar cross section at high rotation number. Applied Thermal Engineering. 106 (5), 681-696 (2016).
- Li, Y., Deng, H., Tao, Z., Xu, G., Chen, Y. Heat transfer characteristics in a rotating trailing edge internal cooling channel with two coolant inlets. International Journal of Heat Mass Transfer. 105 (2), 220-229 (2017).
- Deng, H., Chen, Y., Tao, Z., Li, Y., Qiu, L. Heat transfer in a two-inlet rotating rectangular channel with side-wall fluid extraction. International Journal of Heat and Mass Transfer. 105 (2), 525-534 (2017).
- You, R., Li, H., Tao, Z., Wei, K. Heat transfer investigation in a smooth rotating channel with thermography liquid crystal. ASME Turbo Expo. GT2016-56413, Turbomachinery Technical Conference and Exposition: Heat Transfer. 5 (B), V05BT16A006 1~10 (2016).
- Morris, W. D., Chang, S. W. An experimental study of heat transfer in a simulated turbine blade cooling passage. International Journal of Heat Mass Transfer. 40 (15), 3703-3716 (1997).
- Chang, S. W., Liou, T. -. M., Po, Y. Coriolis and rotating buoyancy effect on detailed heat transfer distributions in a two-pass square channel roughened by 45° ribs at high rotation numbers. International Journal of Heat Mass Transfer. 53 (7), 1349-1363 (2010).
- Wang, W. J. . Heat transfer in rotating twin-pass trapezoidal-sectioned passage with two opposite walls roughened by 45 degree ribs. , (2006).
- Chang, S. W., Wu, P. -. S., Chen, C. -. S., Weng, C. -. C., Jiang, Y. -. R., Shih, S. -. H. Thermal performance of radially rotating two-pass S-shaped zig-zag channel. International Journal of Heat and Mass Transfer. 115 (B), 1011-1031 (2017).
- Chang, S. W., Lees, A. W., Liou, T. -. M., Hong, G. F. Heat transfer of a radially rotating furrowed channel with two opposite skewed sinusoidal wavy walls. International Journal of Thermal Sciences. 49 (5), 769-785 (2010).
- Chang, S. W., Liou, T. -. M., Lee, T. -. H. Heat transfer of a rotating rectangular channel with a diamond-shaped pin-fin array at high rotation numbers. Journal of Turbomachinery Transactions of the ASME. 135 (4), (2013).
- Morris, W. D., Chang, S. W. Heat transfer in a radially rotating smooth-walled tube. The Aeronautical Journal. 102 (1015), 277-285 (1998).
Przedruki i uprawnienia
Zapytaj o uprawnienia na użycie tekstu lub obrazów z tego artykułu JoVE
Zapytaj o uprawnieniaThis article has been published
Video Coming Soon
Copyright © 2025 MyJoVE Corporation. Wszelkie prawa zastrzeżone