É necessária uma assinatura da JoVE para visualizar este conteúdo. Faça login ou comece sua avaliação gratuita.
Method Article
Abordagem de modelagem de elementos finitos baseada em imagem de ultrassom intravascular para quantificar propriedades mecânicas in vivo da artéria coronária humana
* Estes autores contribuíram igualmente
Neste Artigo
Resumo
As imagens de ultrassom intravascular in vivo mostram o movimento transversal coronário correspondente a diferentes condições de carga de pressão. Com base em um modelo de elementos finitos, um esquema iterativo foi empregado para determinar as propriedades mecânicas específicas do paciente das artérias coronárias in vivo, combinando o movimento coronário do modelo computacional e das imagens médicas.
Resumo
A quantificação das propriedades mecânicas das paredes arteriais coronárias pode fornecer informações significativas para o diagnóstico, manejo e tratamento das doenças arteriais coronarianas. Como as amostras coronárias específicas do paciente não estão disponíveis para pacientes que requerem monitoramento contínuo, o teste experimental direto das propriedades do material do vaso torna-se impossível. Os modelos coronários atuais normalmente usam parâmetros de material da literatura disponível, levando a erros significativos de cálculo de tensão/deformação mecânica. Aqui, introduziríamos uma abordagem de atualização baseada em modelo de elementos finitos (FEMBUA) para quantificar as propriedades materiais in vivo específicas do paciente das artérias coronárias com base em imagens médicas. Imagens in vivo de cinessom intravascular (IVUS) e histologia virtual (VH)-IVUS de artérias coronárias foram adquiridas de um paciente com doença arterial coronariana. As imagens de cine IVUS mostrando o movimento vascular ao longo de um ciclo cardíaco foram segmentadas, e dois quadros de IVUS com circunferências de lúmen máxima e mínima foram selecionados para representar a geometria coronariana em condições de pressão sistólica e diastólica, respectivamente. A imagem do VH-IVUS também foi segmentada para obter os contornos dos vasos, e uma espessura de camada de 0,05 cm foi adicionada aos contornos do VH-IVUS para reconstruir a geometria coronariana. Um modelo computacional de elementos finitos foi criado com um modelo de material anisotrópico de Mooney-Rivlin usado para descrever as propriedades mecânicas do vaso e as condições de pressão arterial pulsátil prescritas para a superfície luminal coronária para fazê-la contrair e expandir. Em seguida, uma abordagem de atualização iterativa foi empregada para determinar os parâmetros do material do modelo anisotrópico de Mooney-Rivlin, combinando as circunferências mínima e máxima do lúmen do modelo computacional de elementos finitos com as das imagens cine IVUS. Essa abordagem de atualização baseada em modelo de elementos finitos baseada em imagem pode ser estendida com sucesso para determinar as propriedades do material das paredes arteriais em vários leitos vasculares e tem potencial para avaliação de risco de doenças cardiovasculares.
Introdução
A doença arterial coronariana (DAC) é uma das principais causas de mortalidade e morbidade, sendo responsável por mais de 9,14 milhões de mortes em 2019 em todo o mundo 1,2. O desenvolvimento de doenças arteriais coronarianas, como aterosclerose e estenose, é frequentemente acompanhado por alterações nas forças mecânicas e alterações nas propriedades do material da parede vascular3. As propriedades materiais das artérias coronárias não são apenas a pedra angular para determinar sua resposta mecânica à carga fisiológica, mas também os elementos-chave para simular o comportamento mecânico dos vasos sanguíneos, prever o desenvolvimento de lesões ateroscleróticas e avaliar o efeito terapêutico de vários dispositivos médicos 4,5. Consequentemente, uma compreensão profunda e uma quantificação precisa das propriedades do material coronário são de suma importância para o diagnóstico precoce da doença, medicina de precisão e avaliação do prognóstico6.
Experimentos mecânicos de tecidos coronários isolados, como teste biaxial planar, teste de indentação, teste de insuflação-extensão e teste de extensão uniaxial, são abordagens comuns para quantificar as propriedades mecânicas das paredes dos vasos coronários ex vivo 7,8,9. A partir dessas abordagens, amostras de artérias coronárias foram obtidas de pacientes ou animais experimentais. Testes mecânicos foram realizados para determinar as respostas de deformação da parede do vaso sob diferentes condições de tensão e, em seguida, os parâmetros do material foram determinados ajustando os dados experimentais10. Estudos anteriores mostraram que as propriedades coronarianas são altamente não lineares e anisotrópicas11. Embora os experimentos ex vivo possam fornecer dados precisos sobre as propriedades do material, também existem limitações significativas, que são as seguintes: Primeiro, o comportamento mecânico da amostra após a retirada dos sujeitos vivos seria diferente daquele em condições in vivo, o que pode afetar a precisão dos resultados dos testes. Em segundo lugar, devido a restrições éticas e práticas, é difícil obter uma grande coleção de tecidos normais ou patológicos das artérias coronárias para realizar o teste mecânico.
Para superar essas limitações, os pesquisadores exploraram novas técnicas para quantificação in vivo, em tempo real e específica do paciente das propriedades do material coronário. Entre eles, a abordagem de atualização baseada em modelo de elementos finitos (FEMBUA) baseada em imagens médicas promete abordar essas questões desafiadoras. Essa abordagem faz uso de técnicas avançadas de imagem, como ultrassom intravascular (IVUS) e histologia virtual (VH)-IVUS, para capturar geometria coronariana detalhada, composições de tecidos e seu movimento12. Ao construir modelos 3D de elementos finitos (FE) e incorporar condições fisiológicas de pressão arterial específicas do paciente, o comportamento vascular dinâmico durante os ciclos cardíacos pode ser recuperado otimizando os parâmetros do material para corresponder aos dados da imagem para quantificação rápida e precisa das propriedades do material coronário13. As vantagens da abordagem de atualização de FE in vivo em relação aos experimentos ex vivo incluem avaliação in vivo sem excisão de tecido, facilitando avaliações em larga escala e simulando a dinâmica vascular sob condições complexas para auxiliar na compreensão fisiopatológica das doenças coronarianas.
Neste artigo, são apresentadas as principais etapas da abordagem de atualização baseada em modelo de elementos finitos, que incluem uma segmentação detalhada e processamento de imagens cine IVUS e VH-IVUS, reconstrução do modelo computacional de estrutura de camada fina, execução do esquema iterativo para pesquisar parâmetros de material ideais para tecidos arteriais coronários. O objetivo deste protocolo é quantificar as propriedades do material da artéria coronária de uma amostra de paciente com DAC usando o método FEMBUA como demonstração, especialmente a ilustração de métodos passo a passo. Concluímos discutindo o significado e outros aspectos desse método in vivo .
A participante selecionada é uma mulher de 64 anos sem história clínica prévia de doença arterial coronariana. Este paciente foi diagnosticado com doença arterial coronariana após apresentar sintomas de dor torácica. A angiografia coronariana e o exame de USIC foram realizados para confirmar o diagnóstico. Uma lesão em placa com estenose de 60% foi encontrada no meio da artéria descendente anterior. Após a avaliação, a terapia médica ideal foi adotada para tratar o paciente.
Protocolo
Dados clínicos não identificados, incluindo imagens de IVUS in vivo e dados de pressão arterial, foram adquiridos de um paciente com DAC no Zhongda Hospital, Southeast University, com consentimento informado obtido. A amostra de pacientes foi selecionada a partir do grupo de pacientes de um estudo clínico sobre lesões ateroscleróticas coronarianas intermediárias para demonstrar o método de quantificação das propriedades materiais dos vasos coronários específicos do paciente14. O estudo foi conduzido seguindo o protocolo aprovado pelo Comitê de Ética em Pesquisa Clínica do Hospital Zhongda, Southeast University (número de aprovação: 2017ZDSYLL023-p01).
1. Aquisição e processamento de dados
- Aquisição de imagens Cine IVUS e VH-IVUS
- Coloque o cateter IVUS distal à lesão aterosclerótica com a orientação de uma angiografia coronária e puxe-o de volta para o lado proximal. Gere imagens IVUS em escala de cinza ao longo do caminho para visualizar a seção transversal do vaso coronário.
- Use o sistema de imagem IVUS equipado com um cateter de platina 2,9F de 20 MHz de alto desempenho para adquirir imagens IVUS do segmento arterial coronário com placa aterosclerótica do paciente com DAC (Figura 1).
- Durante a aquisição da imagem de IVUS, pause o cateter no local da lesão pré-selecionado por aproximadamente 2 s para obter uma sequência de imagens de IVUS chamada cine IVUS. As imagens cine IVUS mostraram claramente as mudanças transversais dinâmicas no local da placa ao longo do ciclo cardíaco.
- Gere imagens VH-IVUS com base em quadros IVUS adquiridos no instante do pico R em eletrocardiogramas para visualizar os componentes da placa em forma codificada por cores usando o sistema de imagem.
NOTA: As imagens VH-IVUS fornecem um mapa de cores intuitivo para quatro componentes-chave da placa na placa aterosclerótica: núcleo necrótico rico em lipídios (lipídio) em vermelho, calcificação em branco, tecido fibroso em verde escuro e tecido adiposo fibroso em verde claro. - Salve imagens VH-IVUS e cine IVUS no formato DICOM para análise offline.
- Segmentação e processamento de imagens
- Abra arquivos DICOM usando o visualizador, clique duas vezes no Nome da sequência correspondente para abrir a imagem e clique em Exportar > Exportar imagens para salvar cada quadro cine IVUS ou quadro VH-IVUS como uma imagem individual no formato BMP. Cada imagem BMP contém 500 x 500 pixels, conforme indicado pelo arquivo DICOM original.
- Examine a imagem cine IVUS quadro a quadro para encontrar os quadros consecutivos obtidos no local da placa pré-selecionada durante um ciclo cardíaco. Havia 26 quadros de cine IVUS gerados durante um ciclo cardíaco para este local de placa de amostra.
- Examine todas as imagens VH-IVUS geradas para encontrar a imagem VH-IVUS obtida no local da placa fornecida. As imagens VH-IVUS usadas aqui foram criadas usando um quadro de IVUS a partir dos quadros de cine IVUS em um ciclo cardíaco.
- Segmente imagens de VH-IVUS e cine IVUS usando o software ImageJ para obter os contornos dos limites dos vasos e dos componentes da placa (ver Figura 1C).
- Selecione a guia Linha reta > segmentada e delineie manualmente os contornos do lúmen, o limite externo do vaso coronário e os componentes da placa em imagens cine IVUS e VH-IVUS. Para a imagem cine IVUS, segmente apenas os contornos do lúmen e do limite externo do vaso, enquanto para a imagem VH-IVUS, segmente os contornos do lúmen, limite externo do vaso e limites dos componentes da placa.
- Para simplificar, mantenha apenas grandes componentes lipídicos para gerar um modelo de elementos finitos e ignore componentes lipídicos pequenos e isolados. Apenas um lipídio estava presente nesta amostra de placa. Sobreponha os contornos delineados nas imagens originais usando a sobreposição de > imagem > a guia Adicionar seleção .
- Navegue até o menu To ROI Manager para gerenciar contornos, ajustar propriedades e definir cores e largura de linha para valores adequados para melhor visualização. Selecione a guia Propriedades , defina a cor do traçado para uma cor diferente e preencha a largura da linha na largura. Aqui, defina as cores da linha como verde, azul e vermelho para os contornos do lúmen, do limite externo e do lipídio, respectivamente, e a largura da linha como 3.
- Suavize contornos usando Editar > seleção > Ajustar spline na barra de comando depois de selecionar um contorno específico para obter um contorno suave. Esta operação utiliza técnicas de ajuste de curva spline para suavizar automaticamente os contornos.
- Clique em Arquivo > Salvar como > guia Coordenadas XY para salvar as coordenadas de ponto de cada contorno, como lúmen, limite externo e componente de placa, em um arquivo txt separado. Este arquivo contém os valores das coordenadas x e y dos pontos que constituem o contorno, com pixels como unidade.
- Registre o tamanho físico real de cada pixel em imagens cine IVUS e VH-IVUS (indicado como tamanho do pixel) do arquivo DICOM. A distância real de um pixel nos dados IVUS usados aqui é de 0,002 cm. Essas informações seriam usadas para converter as coordenadas do ponto com o pixel como unidade em distância real com cm como unidade.
- Processamento de dados de contorno
- Processamento de dados de contorno Cine IVUS
- Leia arquivos txt de contornos de lúmen de todas as imagens de cine IVUS em um ciclo cardíaco com MATLAB.
- Multiplique todos os contornos do lúmen pelo tamanho do pixel para obter o tamanho real dos contornos do lúmen.
- Calcule as circunferências do lúmen para todos os contornos do lúmen e identifique os quadros IVUS com circunferências de lúmen máxima (Cmax) e mínima (Cmin), representando condições diastólicas e sistólicas, respectivamente.
- Processamento de dados de contorno VH-IVUS
- Leia arquivos txt dos contornos dos componentes do lúmen, limite externo e placa da imagem VH-IVUS com MATLAB.
- Multiplique todos os contornos pelo tamanho do pixel para obter o tamanho real de todos os contornos.
- Divida novamente cada contorno em 100 pontos igualmente espaçados e execute a suavização 2D para obter novos dados de contorno VH-IVUS para substituir os antigos.
- Processamento de dados de contorno Cine IVUS
2. Modelo de elementos finitos
- Reconstrução da geometria do vaso coronário
- Crie uma camada de contornos no espaço tridimensional adicionando o valor da coordenada z para todos os pontos dos contornos VH-IVUS, incluindo lúmen, limite externo e lipídio, e defina z = 0 para todos os pontos (Figura 2).
- Crie outra camada de contornos adicionando o valor da coordenada z para todos os pontos dos contornos VH-IVUS e redefina z = 0,05 cm para todos os pontos.
NOTA: Essas duas camadas de contornos reconstroem a geometria 3D do vaso coronário para o modelo somente de estrutura de camada fina, adicionando uma espessura de camada fixa de 0,05 cm aos contornos VH-IVUS (Figura 2).
- Geração de malha de elementos finitos
- Crie dois contornos auxiliares interpolando linearmente o lúmen e os contornos do limite externo com pesos 1/3 e 2/3 (Figura 3A) para cada camada.
- Divida a área do vaso em 8 partes circunferenciais e 3 partes radiais (ver Figura 3B) conectando o lúmen/limite externo ao ponto mais próximo no contorno lipídico (por exemplo, pontos A e B na Figura 3B) ou dois contornos auxiliares com linhas radiais.
- Conecte todos os pontos entre as camadas com linhas retas, formando uma estrutura 3D com 3 x 8 volumes (Figura 3B). Divida cada volume usando elementos hexaédricos para gerar a malha de elementos finitos (Figura 3C) e diferentes grupos de materiais (Figura 3D).
- Execute uma análise de malha refinando a densidade da malha em 10% até que as alterações nas soluções < 5%.
- Definição de propriedade do material
- Use um modelo de material anisotrópico Mooney-Rivlin modificado para descrever as propriedades do material da parede do vaso coronário. Os vasos coronários e os componentes da placa foram considerados materiais hiperelásticos, anisotrópicos, quase incompressíveis e homogêneos, e a função de densidade de energia de deformação do modelo de material anisotrópico modificado de Mooney-Rivlin é:
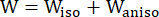 (1)
(1)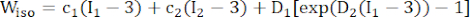 (2)
(2)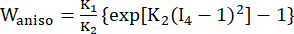 (3)
(3)
onde I1 e I2 são o primeiro e o segundo invariantes do tensor de deformação de Cauchy-Green direito C definido como c = [cij] = XTX, X = [Xij] = [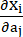 ], (Xi) era a posição atual (aj) era a posição original, I4 = cij(nc)i(nc)j, nc era o vetor unitário na direção circunferencial do vaso. c1, c2, D1, D2, K1 e K2 foram parâmetros de material específicos do paciente.
], (Xi) era a posição atual (aj) era a posição original, I4 = cij(nc)i(nc)j, nc era o vetor unitário na direção circunferencial do vaso. c1, c2, D1, D2, K1 e K2 foram parâmetros de material específicos do paciente. - Atribua os valores iniciais dos parâmetros do material para um vaso coronário específico do paciente de acordo com os resultados do teste biaxial ex vivo, ou seja, c1 = −1.312,9 kPa, c2 = 114,7 kPa, D1 = 629,7 kPa, D2 = 2,0, K1 = 35,9 kPa e K2 = 23,5 (Figura 4A-B)13,15.
- Atribua os parâmetros do material para o componente de placa, se houver. Mais especificamente, para lipídios, c1=0,5 kPa, c2=0, D1=0,5 kPa e D2=1,5; para calcificação, usamos c1=920 kPa, c2=0, D1=360 kPa e D2=2,0 (Figura 4B)16.
NOTA: Os componentes da placa (lipídios e calcificação) foram considerados hiperelásticos, isotrópicos e quase incompressíveis, e suas propriedades mecânicas foram descritas pelo modelo isotrópico de material de Mooney-Rivlin com as funções de densidade de energia de deformação fornecidas na fórmula (2).
- Use um modelo de material anisotrópico Mooney-Rivlin modificado para descrever as propriedades do material da parede do vaso coronário. Os vasos coronários e os componentes da placa foram considerados materiais hiperelásticos, anisotrópicos, quase incompressíveis e homogêneos, e a função de densidade de energia de deformação do modelo de material anisotrópico modificado de Mooney-Rivlin é:
- Equações governantes e configuração de condições de contorno
- Defina as equações governantes para o modelo somente de estrutura de camada fina, que inclui equação de movimento, relação de deformação-deslocamento não linear de Cauchy-Green e modelo de material do vaso coronário11.
- Prescreva formas de onda de pressão arterial específicas do paciente na superfície do lúmen para simular condições fisiológicas reais ( Figura 4C ). Para obter formas de onda de pressão arterial específicas do paciente, dimensione uma forma de onda de pressão aórtica típica com valores de pressão sistólica e diastólica medidos pelo manguito de braço (Figura 4D).
3. Abordagem de atualização baseada em modelo de elementos finitos para propriedades materiais da artéria coronária específicas do paciente
NOTA: O processo iterativo para determinar as propriedades do material coronário específico do paciente é ilustrado na Figura 5.
- Determine a geometria sem carga correspondente à condição de pressão zero como a geometria inicial para o modelo computacional, encolhendo a geometria coronária reconstruída a partir da imagem VH-IVUS axialmente com uma taxa de encolhimento fixa de 95% e circunferencialmente com encolhimento circunferencial (denotado como S) inicialmente definido como 98%.
NOTA: Como a geometria coronária reconstruída a partir da imagem VH-IVUS estava em condições in vivo com pressão arterial prescrita no lúmen e alongamento axial dos segmentos arteriais coronários distais e proximais amarrados, a geometria coronária in vivo deve encolher circunferencialmente e axialmente para obter a geometria de pressão zero. - Fixe a taxa de encolhimento axial em 95% e atualize o encolhimento circunferencial durante as etapas a seguir.
- Defina a proporção de material (denotada como k) para atribuir as propriedades do material específicas do paciente do vaso coronário como: isto é, c1 = k*(−1.312,9) kPa, c2 = k*114,7 kPa, D1 = k*629,7 kPa, K1 = k*35,9 kPa e fixe D2 = 2,0 e K2 = 23,5.
NOTA: Como apenas dois pontos de dados (circunferências mínima e máxima do lúmen correspondentes às pressões diastólica e sistólica) foram obtidos para determinar os parâmetros desconhecidos (taxa de encolhimento circunferencial S e parâmetros do material do modelo de Mooney-Rivlin), reduzimos o número de parâmetros desconhecidos assumindo que as propriedades do material específico do paciente in vivo do vaso coronário eram proporcionais à estimativa inicial com a proporção de material denotada como k: isto é, c1 = k*(−1.312,9) kPa, c2 = k*114,7 kPa, D1 = k*629,7 kPa, K1 = k*35,9 kPa, enquanto D2 = 2,0 e K2 = 23,5 foram fixos. - Atualize o valor k definido para um valor inicial k de 1 junto com a taxa de encolhimento circunferencial S durante o procedimento iterativo a seguir.
- Execute um software para resolver o modelo computacional para obter os resultados numéricos.
- Escreva todos os comandos para criar o modelo somente de estrutura de camada fina em um arquivo em lote (Arquivo Suplementar 1) usando o MATLAB.
- Carregue esse arquivo em lote usando a AUI (interface de usuário avançada) para gerar o modelo (Figura 6A). Resolva o modelo somente de estrutura de camada fina clicando em Arquivo de Dados/Solução e salve-o como um arquivo .dat (Figura 6C). Simule três ciclos cardíacos e adote a solução no último ciclo para apresentar resultados numéricos.
- Exporte os resultados das coordenadas do nó para um arquivo txt navegando Lista > Lista de valores > Zona e selecionando X-POSITION, Y-POSITION e Z-POSITION em Variáveis a serem listadas em Coordenada. Clique em Aplicar e Exportar para exportar os resultados das coordenadas.
- Salve os dados de contorno do lúmen correspondentes às condições de pressão diastólica e sistólica em arquivos .txt para cálculos da circunferência do lúmen.
- Compare as circunferências do lúmen calculadas pelo modelo FE (modelo somente de estrutura de camada de corte fino) na condição de pressão diastólica com dados de cine IVUS in vivo (Cmin) e verifique se o erro relativo foi de <1%. Se a condição foi atendida, vá para a próxima etapa ou atualize a proporção de material k usando o método secante e vá para a etapa 3.3 para executar novamente17,18.
NOTA: No primeiro iterativo, o método de Newton foi usado para atualizar a proporção do material em vez do método secante. - Comparar as circunferências do lúmen calculadas pelo modelo FE na condição de pressão sistólica com os dados de cine IVUS in vivo (Cmax) e verificar se o erro relativo foi de <1%. Em caso afirmativo, interrompa o procedimento iterativo ou atualize a taxa de encolhimento circunferencial S e redirecione para a etapa 3.4 para executar novamente.
NOTA: No primeiro iterativo, o método de Newton foi usado para atualizar a taxa de encolhimento circunferencial em vez do método secante. - Registre os valores ideais de S e k e calcule os parâmetros de material correspondentes do modelo de material Mooney-Rivlin.
- Traçar as curvas circunferenciais e axiais da relação tensão-estiramento do vaso coronário (Figura 7), que podem ser derivadas da seguinte forma:
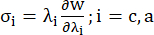 (4)
(4)
onde σ representa a tensão de Cauchy, λ representa a razão de estiramento, i = c, a representa as direções circunferencial e axial.- Para desenhar uma curva de material em uma direção específica, fixe a taxa de estiramento na outra direção para 1. Calcule o módulo de Young efetivo na circunferencial e axial (rotulados YMc e YMa, respectivamente) como a inclinação da função de escala da curva do material no intervalo da razão de estiramento [1,0, 1,1] para refletir a rigidez geral do material da artéria coronária13:
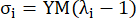 (5)
(5)
- Para desenhar uma curva de material em uma direção específica, fixe a taxa de estiramento na outra direção para 1. Calcule o módulo de Young efetivo na circunferencial e axial (rotulados YMc e YMa, respectivamente) como a inclinação da função de escala da curva do material no intervalo da razão de estiramento [1,0, 1,1] para refletir a rigidez geral do material da artéria coronária13:
- Extraia as distribuições de tensão/deformação da placa a qualquer momento e registre a distribuição dos nós e os valores máximos de tensão durante as fases sistólica e diastólica (Figura 8).
Resultados
Descrevemos em detalhes o método FEMBUA, que permite a análise rápida do material da placa e da tensão das placas coronárias após imagens de IVUS em tempo real e pode determinar as propriedades do material in vivo e os resultados biomecânicos das placas. Os parâmetros do material in vivo do modelo de material de Mooney-Rivlin para este vaso coronário são fornecidos na Tabela 1. Os resultados da simulação do modelo de elementos finitos, inclu...
Discussão
Etapas críticas no protocolo
A etapa mais crítica na abordagem de atualização baseada em modelo de elementos finitos está no procedimento iterativo. Na abordagem, o modelo de elementos finitos deve recuperar com precisão o movimento do vaso coronário na seção transversal vascular a partir de imagens de cine IVUS in vivo . Para isso, minimizar a diferença da circunferência do lúmen entre o modelo de elementos finitos e as imagens in vivo f...
Divulgações
Os autores declaram não haver conflito de interesses.
Agradecimentos
Esta pesquisa foi apoiada em parte pelo Projeto de Ciência e Tecnologia de Saúde Médica da Província de Shandong (nº 202425020256 e 202403010254), Fundação Nacional de Ciências Naturais da China concede 11972117 e 11802060, a Fundação de Ciências Naturais da Província de Jiangsu sob o número de concessão BK20180352 e a Fundação de Ciências Naturais da Província de Shandong sob o número de concessão ZR2024QA110.
Materiais
| Name | Company | Catalog Number | Comments |
| Bee DICOM Viewer | SinoUnion Healthcare Inc. | Version 3.5.1 | A DICOM image reader software |
| ADINA | Adina R & D | Version 9.0 | Finite element solver |
| ImageJ | National Institutes of Health | Segmented IVUS contours | |
| MATLAB | MathWorks | Version R2018a | Commercial programming platform |
| Volcano s5 imaging system | Volcano Company | Intravascular ultrasound imaging system |
Referências
- Roth, G. A., et al. Global burden of cardiovascular diseases and risk factors, 1990-2019: update from the GBD 2019 study. J Am Coll Cardiol. 76 (25), 2982-3021 (2020).
- Kanwar, S. S., et al. Acute coronary syndromes without coronary plaque rupture. Nat Rev Cardiol. 13 (5), 257-265 (2016).
- Milzi, A., et al. Coronary plaque composition influences biomechanical stress and predicts plaque rupture in a morpho-mechanic OCT analysis. Elife. 10, e64020 (2021).
- Stefanati, M., et al. Effect of variability of mechanical properties on the predictive capabilities of vulnerable coronary plaques. Comput Methods Programs Biomed. 254, 108271 (2024).
- Laurent, S., et al. Expert consensus document on arterial stiffness: methodological issues and clinical applications. Eur Heart J. 27 (21), 2588-2605 (2006).
- Daisuke, K., et al. Coronary plaque phenotype associated with positive remodeling. J Cardiovasc Comput Tomogr. 18 (4), 401-407 (2024).
- Macrae, R. A., Miller, K., Doyle, B. J. Methods in mechanical testing of arterial tissue: A review. Strain. 52, 380-399 (2016).
- Hayashi, K. Experimental approaches on measuring the mechanical properties and constitutive laws of arterial walls. J Biomech Eng. 115 (4B), 481-488 (1993).
- Sacks, M. S., Sun, W. Multiaxial mechanical behavior of biological materials. Annu Rev Biomed Eng. 5, 251-284 (2003).
- Charis, C., et al. Impact of combined plaque structural stress and wall shear stress on coronary plaque progression, regression, and changes in composition. Eur Heart J. 40 (18), 1411-1422 (2019).
- Wang, L., et al. Quantifying patient-specific in vivo coronary plaque material properties for accurate stress/strain calculations: An IVUS-based multi-patient study. Front Physiol. 12, 721195 (2021).
- Guo, X. Y., et al. Quantify patient-specific coronary material property and its impact on stress/strain calculations using in vivo IVUS data and 3D FSI models: a pilot study. Biomech Model Mechanobiol. 16 (1), 333-344 (2017).
- Wang, L., et al. Quantification of patient-specific coronary material properties and their correlations with plaque morphological characteristics: An in vivo IVUS study. Int J Cardiol. 371, 21-27 (2023).
- Lu, W., et al. Accurate identification of potential critical coronary lesions for the reduction of risk of cardiovascular events: study protocol for a randomized, open-label, active-controlled multi-center trial. Clin Trial Degenerat Dis. 3 (3), 106-110 (2018).
- Lv, R., et al. Using optical coherence tomography and intravascular ultrasound imaging to quantify coronary plaque cap stress/strain and progression: A follow-up study using 3D thin-layer models. Front Bioeng Biotechnol. 9, 713525 (2021).
- Camasao, D. B., Mantovani, D. The mechanical characterization of blood vessels and their substitutes in the continuous quest for physiological-relevant performances. A critical review. Mater Today Bio. 10, 100106 (2021).
- Holistic Numerical Methods Institute at University of South Florida. . Secant Method. , (2003).
- Barnes, J. An algorithm for solving nonlinear equations based on the secant method. Comp J. 8 (8), 66-72 (1965).
- Liu, M., Liang, L., Sun, W. A new inverse method for estimation of in vivo mechanical properties of the aortic wall. J Mech Behav Biomed Mater. 72, 148-158 (2017).
- Yu, H., et al. Patient-specific in vivo right ventricle material parameter estimation for patients with tetralogy of Fallot using MRI-based models with different zero-load diastole and systole morphologies. Int J Cardiol. 276, 93-99 (2019).
- Meuwissen, M. H. H., Oomens, C. W. J., Baaijens, F. P. T., Petterson, R., Janssen, J. D. Determination of the elasto-plastic properties of aluminium using a mixed numerical-experimental method. J Mater Process Technol. 75, 204-211 (1998).
- Davis, F. M., Luo, Y., Avril, S., Duprey, A., Lu, J. Local mechanical properties of human ascending thoracic aneurysms. J Mech Behav Biomed Mater. 61, 235-249 (2016).
- Fan, L., Wang, H., Kassab, G. S., Lee, L. C. Review of cardiac-coronary interaction and insights from mathematical modeling. WIREs Mech Dis. 16 (3), e1642 (2024).
- Andreas, W., et al. A finite element updating approach for identification of the anisotropic hyperelastic properties of normal and diseased aortic walls from 4D ultrasound strain imaging. J Mech Behav Biomed Mater. 58, 122-138 (2016).
- Liu, M., et al. Identification of in vivo nonlinear anisotropic mechanical properties of ascending thoracic aortic aneurysm from patient-specific CT scans. Sci Rep. 9, 12983 (2019).
- Trabelsi, O., Duprey, A., Favre, J. P., Avril, S. Predictive models with patient specific material properties for the biomechanical behavior of ascending thoracic aneurysms. Ann Biomed Eng. 44, 84-98 (2016).
- Cosentino, F., et al. On the role of material properties in ascending thoracic aortic aneurysms. Comput Biol Med. 109, 70-78 (2019).
- Krauz, K., et al. The role of epicardial adipose tissue in acute coronary syndromes, post-infarct remodeling and cardiac regeneration. Int J Mol Sci. 25 (7), 3583 (2024).
- McCracken, I. R., Smart, N. Control of coronary vascular cell fate in development and regeneration. Semin Cell Dev Biol. 155 (Pt C), 50-61 (2024).
- Holzapfel, G. A., et al. Determination of layer-specific mechanical properties of human coronary arteries with nonatherosclerotic intimal thickening and related constitutive modeling. Am J Physiol Heart Circ Physiol. 289 (5), H2048-H2058 (2005).
- Han, Y., et al. Ventricle stress/strain comparisons between Tertalogy of Fallot patients and healthy using models with different zero-load diastole and systole morphologies. PLoS One. 14 (8), e0220328 (2019).
- Ryo, K., et al. Role of the low-density lipoprotein-cholesterol/high-density lipoprotein-cholesterol ratio in predicting serial changes in the lipid component of coronary plaque. Circ J. 81 (10), 1439-1446 (2017).
- Thomas, T. W., et al. In vivo characterization and quantification of atherosclerotic carotid plaque components with multidetector computed tomography and histopathological correlation. Arterioscler Thromb Vasc Biol. 26 (10), 2366-2372 (2006).
- Masanori, K., et al. In vivo quantitative tissue characterization of human coronary arterial plaques by use of integrated backscatter intravascular ultrasound and comparison with angioscopic findings. Circulation. 105 (21), 2487-2492 (2002).
- Roach, M. R., Burton, A. C. The reason for the shape of the distensibility curves of arteries. Can J Biochem Physiol. 35, 681-690 (1957).
- Fung, Y. C., Liu, S. Q. Strain distribution in small blood vessel with zero-stress state taken into consideration. Am J Physiol. 262, 544-552 (1992).
- Ohayon, J., et al. Influence of residual stress/strain on the biomechanical stability of vulnerable coronary plaques: Potential impact for evaluating the risk of plaque rupture. Am J Physiol Heart Circ Physiol. 293, 1987-1996 (2007).
Reimpressões e Permissões
Solicitar permissão para reutilizar o texto ou figuras deste artigo JoVE
Solicitar PermissãoExplore Mais Artigos
This article has been published
Video Coming Soon
Copyright © 2025 MyJoVE Corporation. Todos os direitos reservados