Уравнение Аррениуса соотносит энергию активации и константу скорости, k, для химических реакций. В уравнении Аррениуса k = AE-EA/RT, R — идеальная газовая константа, которая имеет значение 8.314 Дж/моль·K, T — температура на шкале Кельвина, EA — энергия активации в Дж/моле, e — константа 2.7183, а A — константа, называемая частотным коэффициентом, которая связана с частотой столкновений и ориентацией реагирующих молекул.
Уравнение Аррениуса можно использовать для вычисления энергии активации реакции на экспериментальных кинетических данных. Удобный подход к определению EA для реакции предполагает измерение k при двух или более различных температурах. В ней используется модифицированная версия уравнения Аррениуса, которая принимает форму линейного уравнения:
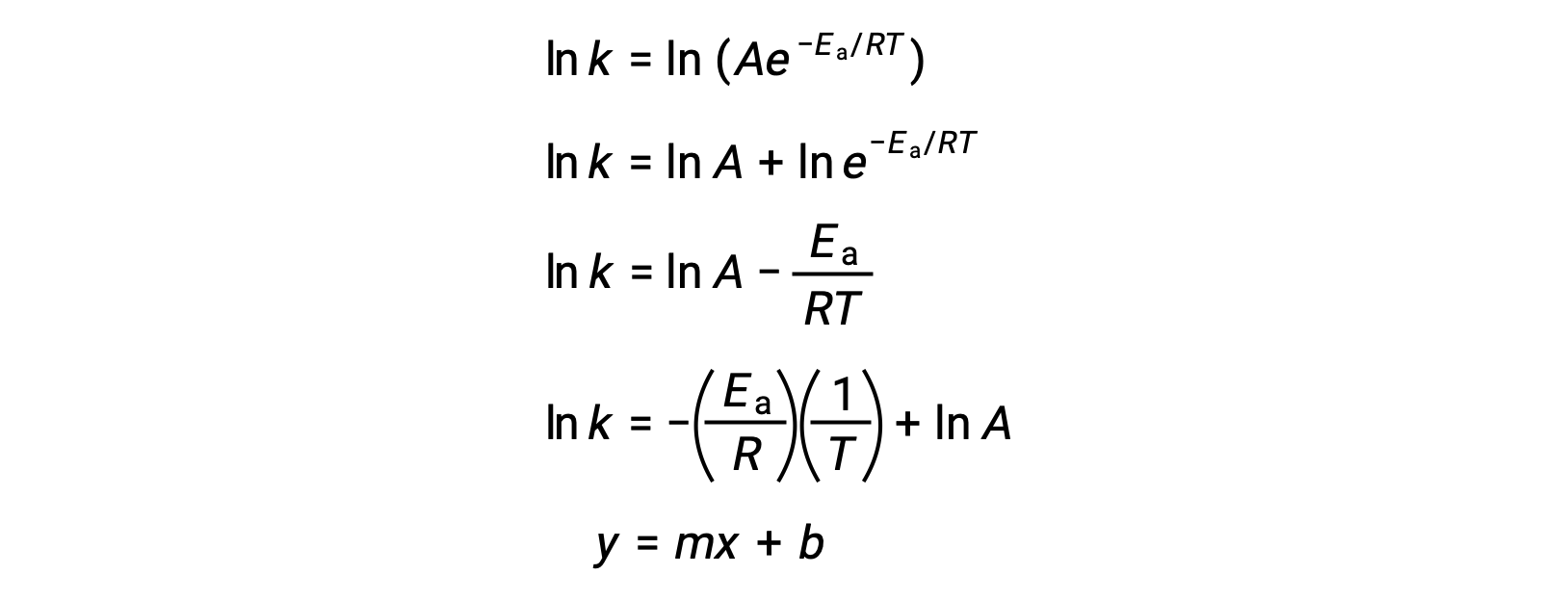
График ln k в сравнении с 1/T линейный с уклоном, равным -a/R и y-отсекаемый равным ln A.
Рассмотрим следующую реакцию:
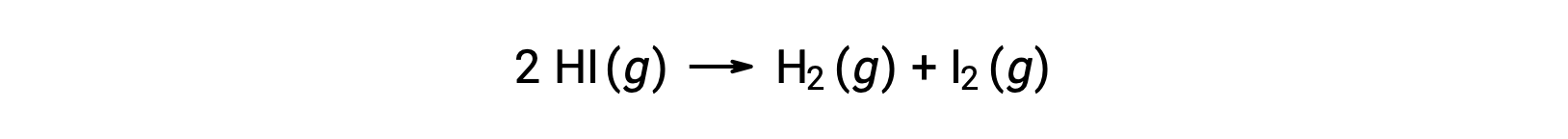
Энергия активации этой реакции может быть определена, если изменение постоянной скорости с температурой известно из кинетических данных реакции, как показано на рисунке.
| Температура (K) | Постоянная скорости (л/моль/с) |
| 555 | 3.52 × 10–7 |
| 575 | 1.22 × 10–6 |
| 645 | 8.59 × 10–5 |
| 700 | 1.16 × 10–3 |
| 781 | 3.95× 10–2 |
Предоставленные данные могут быть использованы для получения значений обратной от температуры (1/T) и природного лога k (ln k).
| 1/T (K–1) | ln k |
| 1.80 × 10–3 | –14.860 |
| 1.74 × 10–3 | –13.617 |
| 1.55 × 10–3 | –9.362 |
| 1.43 × 10–3 | –6.759 |
| 1.28 × 10–3 | –3.231 |
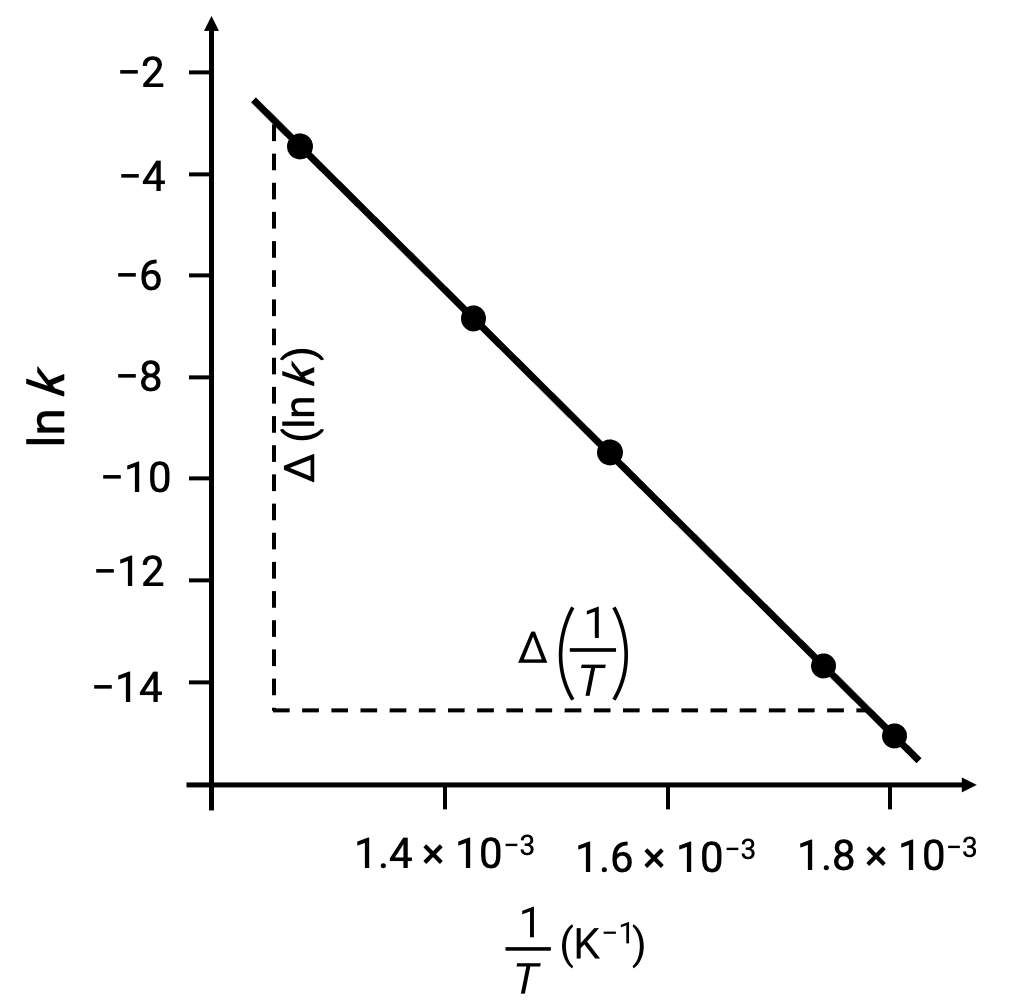
На графике производных точек данных с ln k по сравнению с 1/T создается линейный график, показанный линейной зависимостью между ln k и 1/T, как показано на рисунке.
Наклон линии, соответствующий энергии активации, можно оценить с помощью двух экспериментальных пар данных.

Альтернативный подход к извлечению энергии активации предполагает использование постоянной скорости при двух различных температурах. При таком подходе уравнение Аррениуса переупорядочено до удобной двухточечной формы:
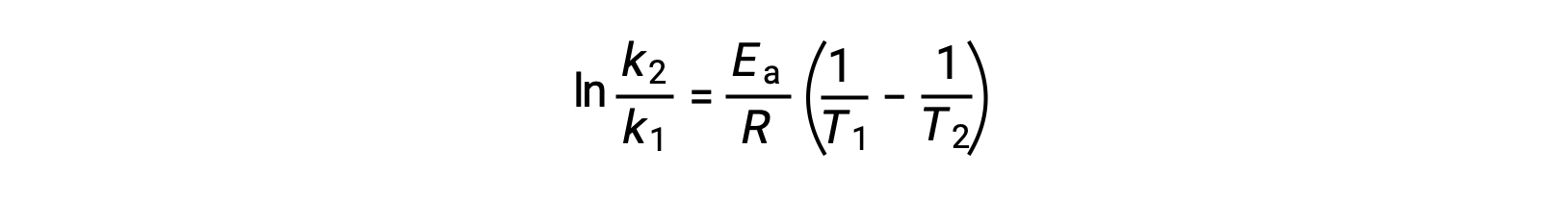
При перестановке уравнения генерируется выражение для энергии активации.
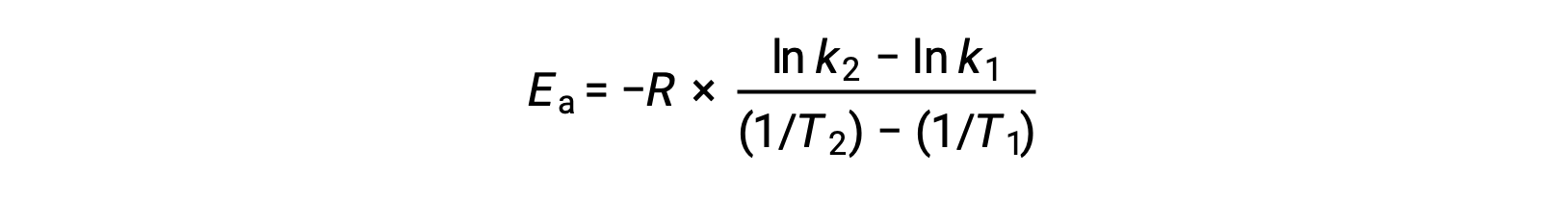
Подстановка двух пар данных и дальнейшие расчеты дают значение энергии активации в джоулях на моль или киложоулях на моль.
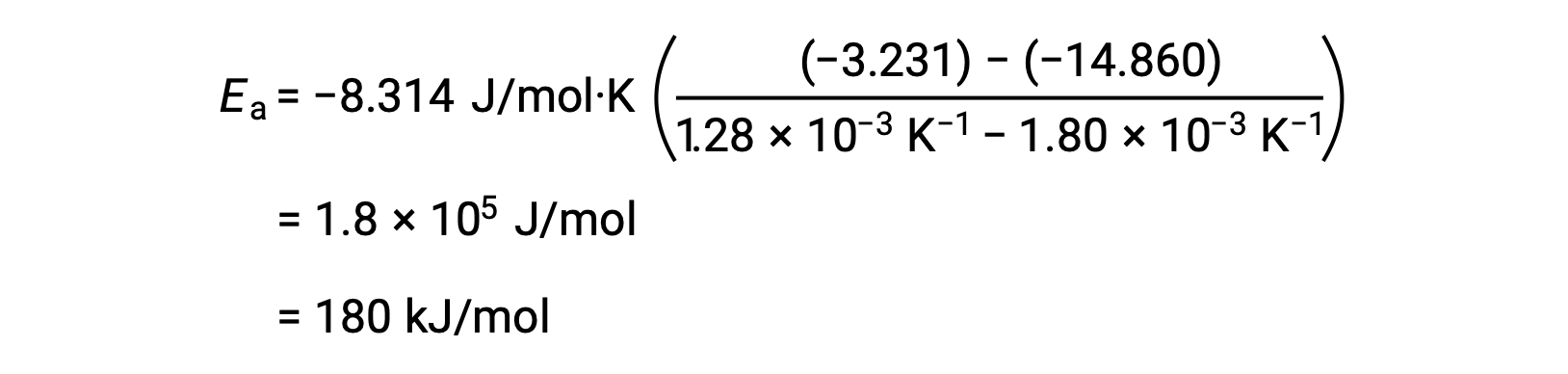
Этот альтернативный двухточечный подход дает тот же результат, что и графический подход. Однако на практике графический подход обычно обеспечивает более надежные результаты при работе с фактическими экспериментальными данными.
Этот текст адаптирован из Openstax, Химия 2е изд., раздел 12.5: Теория столкновений.
Теги
Из главы 13:

Now Playing
13.8 : Графики Аррениуса
Химическая кинетика
37.1K Просмотры

13.1 : Скорость реакции
Химическая кинетика
49.8K Просмотры

13.2 : Измерение скорости реакции
Химическая кинетика
23.7K Просмотры

13.3 : Закон о концентрации и скорости
Химическая кинетика
29.1K Просмотры

13.4 : Определение порядка реакции
Химическая кинетика
54.0K Просмотры

13.5 : Закон интегрированной скорости: зависимость концентрации от времени
Химическая кинетика
33.5K Просмотры

13.6 : Период полураспада реакции
Химическая кинетика
33.3K Просмотры

13.7 : Зависимость температуры от скорости реакции
Химическая кинетика
80.2K Просмотры

13.9 : Механизмы реакции
Химическая кинетика
24.6K Просмотры

13.10 : Шаги, определяющие скорость
Химическая кинетика
30.9K Просмотры

13.11 : Катализ
Химическая кинетика
26.0K Просмотры

13.12 : Ферменты
Химическая кинетика
79.8K Просмотры
Авторские права © 2025 MyJoVE Corporation. Все права защищены