Поверхностное картирование похожих на Землю экзопланет с использованием однотокных кривых света

Резюме

Протокол извлекает информацию из световых кривых экзопланет и строит их поверхностные карты. Он использует световые кривые Земли, которая служит прокси-экзопланетой, чтобы продемонстрировать подход.

Аннотация

Пространственно разрешающие особенности экзопланет с одной точки наблюдений имеет важное значение для оценки потенциальной обитаемости экзопланет. Конечная цель этого протокола заключается в том, чтобы определить, имеют ли эти планетарные миры геологические особенности и/или климатические системы. Мы представляем метод извлечения информации из многоволновых однотасовых кривых света и извлечения карт поверхности. Он использует разложение особого значения (SVD) для отдельных источников, которые способствуют изменению кривой света и сделать вывод о существовании частично облачных климатических систем. С помощью анализа тайм-ряда, полученного из СВД, физические атрибуции основных компонентов (ПК) могут быть выведены без предположений о каких-либо спектральных свойствах. В сочетании с геометрией просмотра можно реконструировать карты поверхности, если будет установлено, что один из ПК содержит информацию о поверхности. Вырождение возникло в результате свертки геометрии пикселей, а информация о спектре определяет качество реконструированных карт поверхности, что требует введения хлализации. Для демонстрации протокола анализируются многоволновые световые кривые Земли, которая служит прокси-экзопланетой. Сравнение результатов и наземной истины представлено, чтобы показать производительность и ограничение протокола. Эта работа служит ориентиром для будущего обобщения приложений экзопланет.

Введение

Выявление обитаемых миров является одной из конечных целей в астробиологии¹. С момента первого^{обнаружения 2,}более 4000 экзопланет были подтверждены^{на сегодняшний день 3} с рядом аналогов Земли (например, TRAPPIST-1e)⁴. Эти планеты имеют орбитальные и планетарные свойства, аналогичные свойствам Земли, и поэтому потенциально пригодны для жизни. В этом контексте важно оценить их обитаемость на основе ограниченных наблюдений. Основываясь на знаниях о жизни на Земле, геологические и климатические системы имеют решающее значение для обитаемости, которая поэтому может служить биоподписями. В принципе, особенности этих систем можно наблюдать на расстоянии, даже если планета не может быть решена пространственно лучше, чем одна точка. В этом случае при оценке обитаемости экзопланет важное значение имеет определение геологических особенностей и климатических систем по одноофиционные световые кривые. Поверхностное картирование этих экзопланет становится актуальным.

Несмотря на сверток между геометрией обзора и спектральными особенностями, информация о поверхности экзопланеты содержится в ее решенных по времени одночаостных световых кривых, которые могут быть получены издалека и получены с достаточными наблюдениями. Тем не менее, двумерное (2D) картирование поверхности потенциально обитаемых похожих на Землю экзопланет является сложной задачей из-за влияния облаков. Методы извлечения 2D-карт были разработаны и испытаны с использованием смоделированных кривых^{света и известных спектров 5,6,7,8,}но они не были применены к реальным наблюдениям. Кроме того, при анализе наблюдений экзопланет в настоящее время и в ближайшем будущем предположения о характерных спектрах могут быть спорными, когда составы поверхности планеты не сильно ограничены.

В этой статье мы демонстрируем метод картирования поверхности для похожих на Землю экзопланет. Мы используем SVD для оценки и отделить информацию из различных источников, которая содержится в многоволновых кривых света без предположений каких-либо конкретных спектров. В сочетании с геометрией просмотра мы представляем реконструкцию поверхностных карт с использованием своевременной, но пространственно запутанной информации о поверхности. Для демонстрации этого метода анализируются двухлетние многоволновые одночастные наблюдения Земли, полученные обсерваторией глубокого космического климата/Камерой полихромной визуализации Земли (DSCOVR/EPIC; www.nesdis.noaa.gov/DSCOVR/spacecraft.html). Мы используем Землю в качестве прокси-экзопланеты для оценки этого метода, поскольку имеющихся в настоящее время наблюдений за экзопланетами недостаточно. В качестве примера мы прикрепляем код к документу. Он разработан под python 3.7 с анакондой и healpy пакеты, но математика протокола также может быть сделано в других средах программирования (например, IDL или MATLAB).

протокол

1. Настройка программирования

1. Настройка среды программирования для прилагаемого кода. Компьютер с операционной системой Linux не требуется, так как пакет healpy недоступен на Windows. Код не является вычислительно дорогим, поэтому обычный персональный компьютер может обрабатывать протокол.
2. Следуйте инструкциям (https://docs.anaconda.com/anaconda/install/linux/), чтобы установить Anaconda с Python 3.7 в систему, а затем использовать следующие команды в терминале для настройки среды программирования:
   $ Конда создать - имя myenv питона 3,7
   $ Конда активировать myenv
   $ Конда установить анаконда
   $ Конда установить healpy
   ПРИМЕЧАНИЕ: Эти шаги могут занять десятки минут в зависимости от аппаратного обеспечения и скорости Интернета. Название среды 'myenv' в первых двух командных строках может быть изменено на любую другую строку.

2. Получение многоволновых кривых света и геометрии просмотра из наблюдений

1. В геометрии просмотра включите долготу и широту суб-звездных и суб-наблюдателей точек для каждого соответствующего срока.
   Чтобы использовать следующий прилагаемый код, убедитесь, что эти два файла имеют тот же формат, что и LightCurve.csv и Geometry.csv.
2. Запустите PlotTimeSeries.py, чтобы визуализировать данные и проверить их качества. Будут созданы две фигуры LightCurve.png и .png (дополнительная цифра 1-2). Параметры в этом и следующих кодах построения, возможно, потребуется скорректировать, если они применяются к различным наблюдениям.
   $ питон PlotTimeSeries.py LightCurve
   $ питон PlotTimeSeries.py геометрия

3. Извлекайте информацию о поверхности из кривых света

1. Центр времени решен многоволновой альбедо световых кривых экзопланеты и нормализовать их соответствующим стандартным отклонением на каждой длине волны. Это приводит к одинаковой важности каждого канала.
   
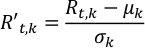
   где_R't,k и R_{t,k являются} масштабируемым и наблюдаемым альбедо на шаге t-th времени и k-th длине волны, соответственно; μ_k и σ_{k являются} средним и стандартным отклонением времени серии альбедо на длине волны k-th.
   1. Запуск Normalize.py для нормализации кривых света, R_t,k. Выход сохраняется в NormalizedLightCurve.csv.
      $ питон Normalize.py
2. Бегите PlotTimeSeries.py, чтобы визуализировать нормализованные кривые света. Будет создана цифра NormalizedLightCurve.png (дополнительная цифра 3).
   $ питон PlotTimeSeries.py НормализованныйLightCurve
3. Применить SVD на масштабируемых кривых света альбедо, чтобы найти доминирующие ПК и их соответствующие серии времени.
   
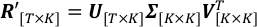
   С левой стороны T и K являются общим числом шагов времени и длин волн наблюдения; R' — это матрица масштабированных наблюдений альбедо, чей (t,k)-й элемент R'_t,k. С правой стороны, колонны V являются ПК, ортонормальные векторы, которые определяют пространство SVD проектов; - это диагональная матрица, элементом которой (k,k)-th является стандартное отклонение масштабируемых кривых света вдоль оси k-th, определяемой k-th колонной V; столбцы U являются соответствующей серии времени каждого ПК в V.
   1. Бегите SingularValueDecomposition.py чтобы разложить R'. В результате U, V ^{T сохраняются} в выходных файлах U.csv, SingularValue.csv и V_T.csv,соответственно.
      $ питон SingularValueDecomposition.py
4. Используйте PlotTimeSeries.py и PlotSVD.py, чтобы визуализировать результат SVD. Будут созданы три фигуры U.png, Sigma.png и V_T.png (дополнительная цифра 4-6).
   $ питон PlotTimeSeries.py U
   $ питон PlotSVD.py
5. Проанализируйте вклады и соответствующие серии времени ПК, чтобы определить тот, который содержит информацию о поверхности.
   1. Сравните значения сингулярного значения по диагонали . Ожидается, что похожая на Землю частично облачная экзопланета будет иметь два сопоставимых доминирующих значения.
      ПРИМЕЧАНИЕ: Может содержать менее или более двух доминирующих значений, которые обсуждаются ниже.
   2. Сравните шаблоны тайм-рядов двух доминирующих ПК. ПК, содержащий информацию о поверхности, имеет более регулярную форму, чем другой. Из-за продольной асимметрии и появления поверхности с небольшими изменениями в течение двух дней подряд, соответствующие серии времени, как правило, имеют примерно постоянную ежедневную вариацию.
   3. Вычислить периодичность двух доминирующих ПК с помощью Lomb-Scargle^{парограмма 9,10,} чтобы подтвердить выбор ПК. ПК, содержащий информацию о поверхности, имеет более высокий пик, соответствующий периоду вращения в спектре плотности мощности.
   4. Вы Periodogram.py, чтобы получить спектры мощности часовой серии каждого ПК. Спектры питания сохраняются в периодограмме.csv.
      $ питон Periodogram.py
   5. Запустите PlotPeriodogram.py, чтобы визуализировать эти парограммы и подтвердить выбор ПК. Будет создана цифра .png (дополнительнаяцифра 7). Текущий код построения добавляет в пунктирной строки, представляющие ежегодные, полугодовые, суточные и полудневые циклы для справки, которые, возможно, потребуется изменить при применении к другим наблюдениям.
      $ питон PlotPeriodogram.py
   6. Выберите ПК, v_j, который содержит информацию о поверхности и его серии времени, u_j.
      
      
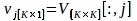
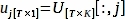
      где V:,jи U:,jявляются j-й колонны V и U, соответственно; j является индексом ПК, выведенным на шаг 3.3, который содержит информацию о поверхности.

4. Построить планетарную карту поверхности

1. Для пикселизации карты извлечения используется метод иерархической пикселизации равной области (HEALPix)^11. Он делит сферическую поверхность планеты на пиксели с той же областью и равномерной распределением. Обозначить неизвестное значение p-th пикселя как x_p.
   1. Запустите HEALPixRandom.py, чтобы визуализировать метод пикселизации. Фигура HEALPixRandom.png будет создана(дополнительная цифра 8). Сторона параметра N_на строке 17 может быть изменена для различных разрешений. Этот шаг может занять от нескольких секунд до нескольких минут в зависимости от разрешения.
      $ питон HEALPixRandom.py
2. Вычислить вес p-th пикселя в наблюдениях на шаге t-th времени, w_t,p, используя геометрию просмотра.
   
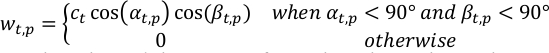
   где α_t,p,β_t,p являются солнечными и космическими зенитами углов на p-й пиксель на шаге t-th времени; c_t — это термин нормализации наблюдения t-th, так что сумма общего веса при каждом шаге времени является единством.
   ПРИМЕЧАНИЕ: Геометрия, как предполагается, известна на этом этапе, или может быть получена из другого анализа, который обсуждается ниже.
   1. Запуск ComputeWeight.py для вычисления w_t,p. Измените значение стороны N_на строке 23 для других разрешений полученной карты. Выход сохраняется как W.npz за счет его размера.
      $ питон ComputeWeight.py
3. Используйте PlotWeight.py, чтобы визуализировать эти веса. В папке Вес будет создан ряд цифр, по одному на каждом этапе времени. Слияние их приводит к Дополнительное видео 1, который показывает, как вес каждого пикселя меняется со временем. Этот шаг может занять несколько часов из-за большого количества визуализаций.
   $ питон PlotWeight.py
4. Объедините геометрию и наблюдения для достижения проблемы линейной регрессии.
   
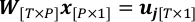
   где P является общим числом извлечения пикселей; W является вес матрицы с w_t,p как (t,p)-й элемент; x состоит из x_{p как} элемент p-th, который является количеством, которое должно быть решено в этой проблеме.
   Решить проблему линейной регрессии с еконкрецией нормы L-2.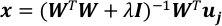
   
   где я матрицы идентичности и является параметром ехализации.
   ПРИМЕЧАНИЕ: 10^-3 является хорошим значением для, когда ТЗ10⁴ и ПЗ3-10³. Они должны быть скорректированы путем сравнения значений двух терминов в локализованной квадратной ошибке, e, как показано ниже.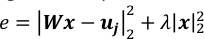
   
   1. Запустите LinearRegression.py, чтобы решить эту линейную проблему регрессии. Результат x сохраняется в файле PixelValue.csv. Измените значение no на линии 16 для различных сильных сторон ехализации.
      $ питон LinearRegression.py
5. Преобразование x в 2D-карту поверхности в соответствии с правилом отображения HEALPix.
   1. Запустите PlotMap.py для построения извлеченных карт с использованием различных параметров ехлализации. С текуще Map_й .png будут созданы три Map_-2.png.png и Map_-4.png (дополнительнаяцифра 9). Взаимосвязь между индексами пикселей и их расположением на карте описана в документе HEALPix^11. Этот шаг занимает десятки секунд.
      $ питон PolotMap.py

5. Оценка неопределенности полученной карты

1. Перепишите проблему линейной регрессии на шаге 4.3 с "истинным значением" x как z и шумом наблюдения, ε.
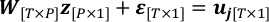
   1. Предположим ε вы должны следовать за гауссийской дистрибуции N (0, σ²Я_{»T »T}» ) и оценить его коварианс. T-P — это степень свободы u_{j от} наблюдения при исправлении полученной карты.
      
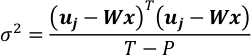
   2. Объедините уравнения в шагах 4.4 и 5.1. Это приводит к гауссийский вектор х.
      
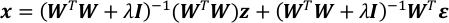
   3. Вычислить ожидание и матрицу коварианса x.
      
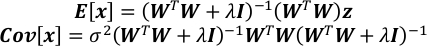
   4. Получите неопределенность каждого элемента в x в качестве квадратного корня соответствующего элемента по диагонали Covи x.
      
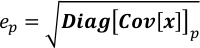
      где e_p является неопределенностью x_p; Диаги Ковхр-й элемент по диагонали Ковхх.
   5. Запуск Covariance.py, чтобы вычислить матрицу коварианса x. Результат сохраняется в Covariance.npz за счет его размера. Этот шаг занимает от десятков секунд до минут в зависимости от размера W.
      $ питон Covariance.py
2. Преобразование e_p в полученную 2D карту в соответствии с правилом отображения HEALPix.
   1. Выйдите PlotCovariance.py, чтобы визуализировать Кови хи карту неопределенности e_p к извлеченной карте. Будут созданы две цифры .png и неопределенность.png (дополнительная цифра 10-11).
      $ питон PlotCovariance.py

Результаты

Мы используем многоволновые однотасные световые кривые Земли для демонстрации протокола и сравнения результатов с наземной истиной для оценки качества картирования поверхности. Наблюдение, используемое здесь, получено DSCOVR/EPIC, который является спутником, расположенным вблизи первой ...

Обсуждение

Одним из важнейших требований протокола является возможность извлечения поверхностной информации из световых кривых, которая зависит от облачного покрытия. В шаге 3.5.1 относительные значения ПК могут отличаться среди экзопланет. В случае с Землей первые два ПК доминируют в вариациях к...

Материалы

Name	Company	Catalog Number	Comments
Python 3.7 with anaconda and healpy packages			Other programming environments (e.g., IDL or MATLAB) also work.