14.6 : Calculating Equilibrium Concentrations

Being able to calculate equilibrium concentrations is essential to many areas of science and technology—for example, in the formulation and dosing of pharmaceutical products. After a drug is ingested or injected, it is typically involved in several chemical equilibria that affect its ultimate concentration in the body system of interest. Knowledge of the quantitative aspects of these equilibria is required to compute a dosage amount that will solicit the desired therapeutic effect.

A more challenging type of equilibrium calculation can be one in which equilibrium concentrations are derived from initial concentrations and an equilibrium constant. For these calculations, a four-step approach is typically useful:

1. Identify the direction in which the reaction will proceed to reach equilibrium.
2. Develop an ICE table.
3. Calculate the concentration changes and, subsequently, the equilibrium concentrations.
4. Confirm the calculated equilibrium concentrations.

Calculation of Equilibrium Concentrations

Under certain conditions, the equilibrium constant K_c for the decomposition of PCl₅(g) into PCl₃(g) and Cl₂(g) is 0.0211. The above procedure can be used to determine the equilibrium concentrations of PCl₅, PCl₃, and Cl₂ in a mixture that initially contained only PCl₅ at a concentration of 1.00 M.

Step 1. Determine the direction the reaction proceeds.

The balanced equation for the decomposition of PCl₅ is

Because only the reactant is present initially, Q_c = 0, and the reaction will proceed to the right.

Step 2. Develop an ICE table.

	     PCl5 (g)    ÂÂÂ	  PCl3 (g)  ÂÂÂ	  Cl2 (g) ÂÂÂ
Initial Concentration (M)	1.00	0	0
Change (M)	−x	+x	+x
Equilibrium Concentration (M)	1.00 − x	x	x

Step 3. Solve for the change and the equilibrium concentrations.

Substituting the equilibrium concentrations into the equilibrium constant equation gives

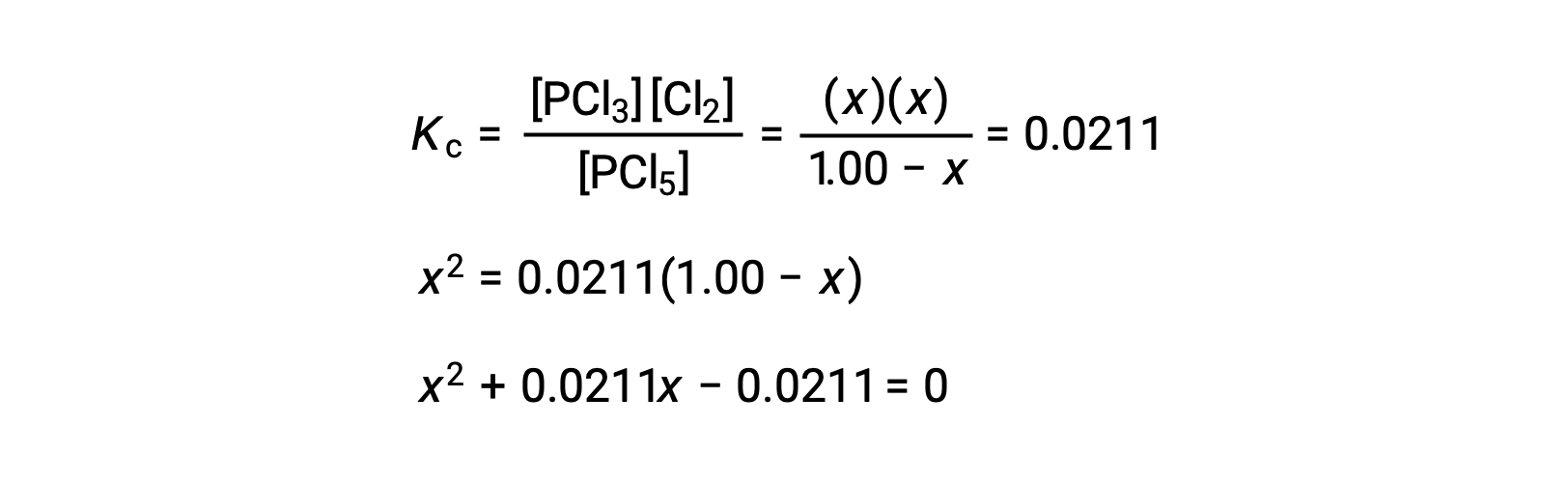
An equation of the form ax² + bx + c = 0 can be rearranged to solve for x:

In this case, a = 1, b = 0.0211, and c = −0.0211. Substituting the appropriate values for a, b, and c yields:

The two roots of the quadratic are, therefore,

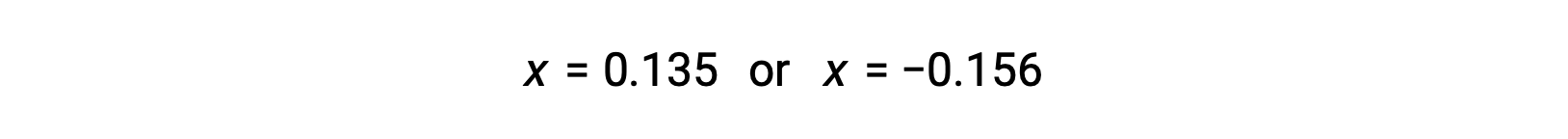
For this scenario, only the positive root is physically meaningful (concentrations are either zero or positive), and so x = 0.135 M. The equilibrium concentrations are

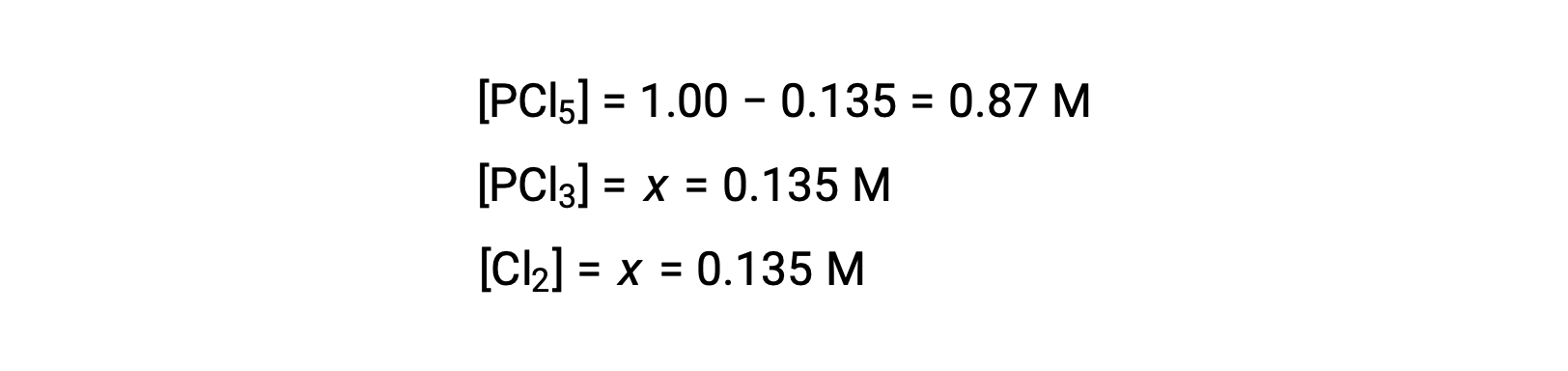
Step 4. Confirm the calculated equilibrium concentrations.

Substitution into the expression for K_c (to check the calculation) gives

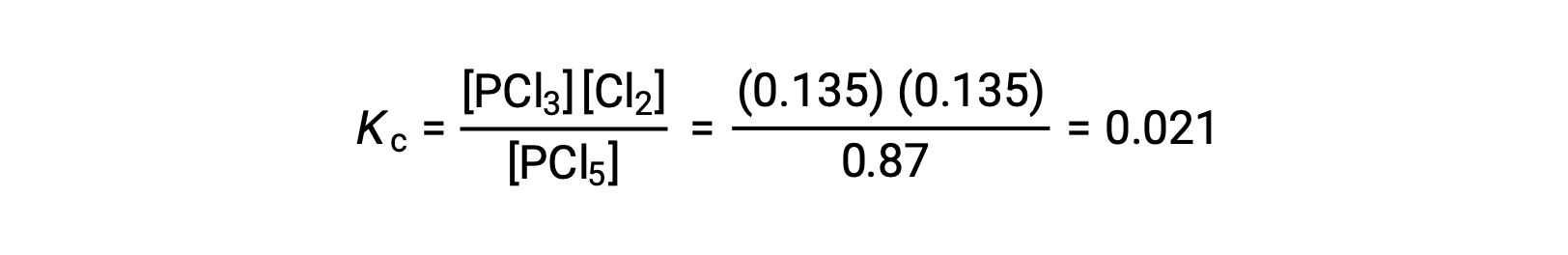
The equilibrium constant calculated from the equilibrium concentrations is equal to the value of K_c given in the problem (when rounded to the proper number of significant figures).

This text has been adapted from Openstax, Chemistry 2e, Section 13.4 Equilibrium Calculations.