11.9 : Clausius-Clapeyron Equation
The equilibrium between a liquid and its vapor depends on the temperature of the system; a rise in temperature causes a corresponding rise in the vapor pressure of its liquid. The Clausius-Clapeyron equation gives the quantitative relation between a substanceâÃÂÃÂs vapor pressure (P) and its temperature (T); it predicts the rate at which vapor pressure increases per unit increase in temperature.
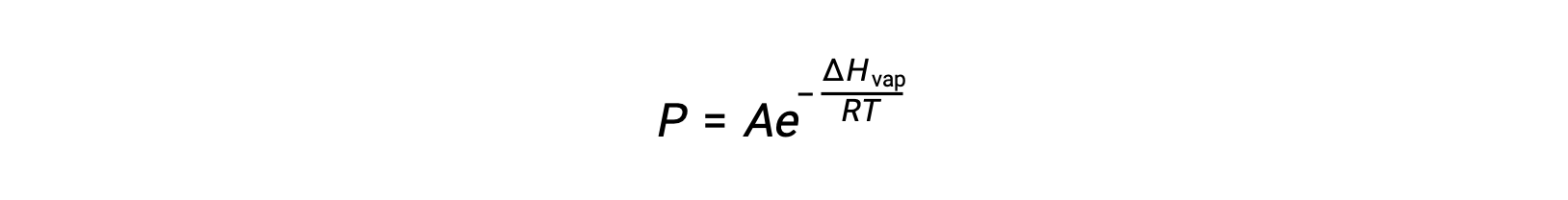
where ÃÂÃÂHvap is the enthalpy of vaporization for the liquid, R is the gas constant, and A is a constant whose value depends on the chemical identity of the substance. Temperature (T) must be in kelvin in this equation. However, since the relationship between vapor pressure and temperature is not linear, the equation is often rearranged into logarithmic form to yield the linear equation:
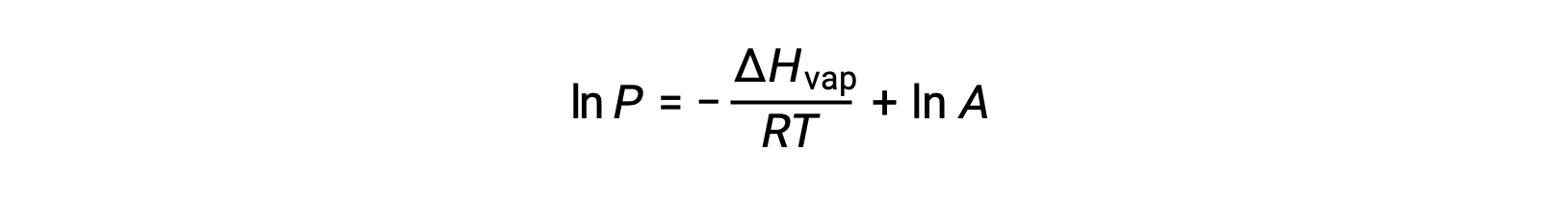
For any liquid, if the enthalpy of vaporization and vapor pressure at a particular temperature is known, the Clausius-Clapeyron equation allows to determine the liquidâÃÂÃÂs vapor pressure at a different temperature. To do this, the linear equation may be expressed in a two-point format. If at temperature T1, the vapor pressure is P1, and at temperature T2, the vapor pressure is P2, the corresponding linear equations are:
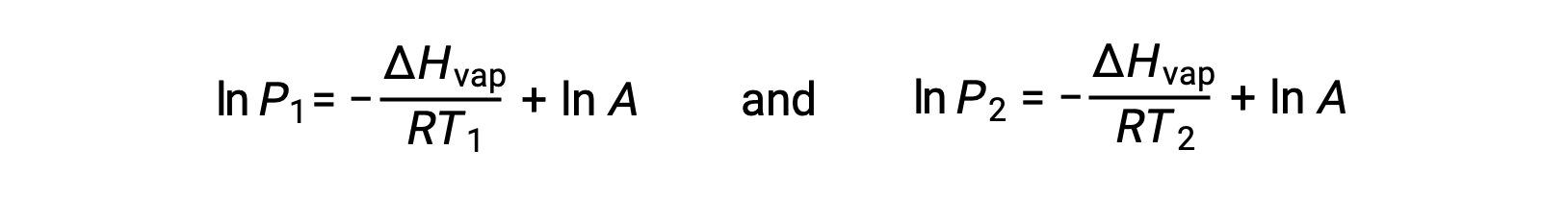
Since the constant, A, is the same, these two equations may be rearranged to isolate ln A and then set them equal to one another:
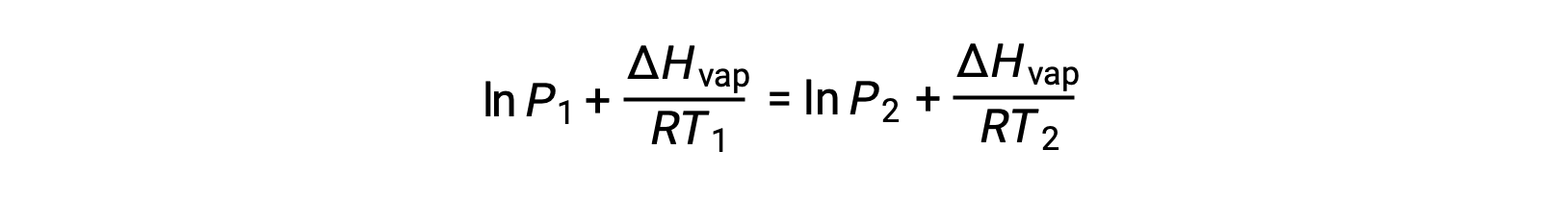
which can be combined into:
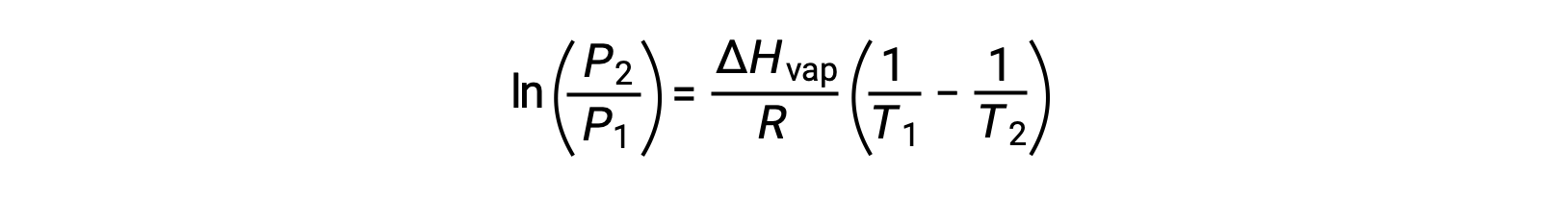
This text is adapted from Openstax, Chemistry 2e, Section 10.3: Phase Transitions.
From Chapter 11:

Now Playing
11.9 : Clausius-Clapeyron Equation
Liquids, Solids, and Intermolecular Forces
55.4K Views

11.1 : Molecular Comparison of Gases, Liquids, and Solids
Liquids, Solids, and Intermolecular Forces
40.3K Views

11.2 : Intermolecular vs Intramolecular Forces
Liquids, Solids, and Intermolecular Forces
85.4K Views

11.3 : Intermolecular Forces
Liquids, Solids, and Intermolecular Forces
56.7K Views

11.4 : Comparing Intermolecular Forces: Melting Point, Boiling Point, and Miscibility
Liquids, Solids, and Intermolecular Forces
43.6K Views

11.5 : Surface Tension, Capillary Action, and Viscosity
Liquids, Solids, and Intermolecular Forces
27.4K Views

11.6 : Phase Transitions
Liquids, Solids, and Intermolecular Forces
18.7K Views

11.7 : Phase Transitions: Vaporization and Condensation
Liquids, Solids, and Intermolecular Forces
17.1K Views

11.8 : Vapor Pressure
Liquids, Solids, and Intermolecular Forces
34.1K Views

11.10 : Phase Transitions: Melting and Freezing
Liquids, Solids, and Intermolecular Forces
12.2K Views

11.11 : Phase Transitions: Sublimation and Deposition
Liquids, Solids, and Intermolecular Forces
16.6K Views

11.12 : Heating and Cooling Curves
Liquids, Solids, and Intermolecular Forces
22.3K Views

11.13 : Phase Diagrams
Liquids, Solids, and Intermolecular Forces
39.2K Views

11.14 : Structures of Solids
Liquids, Solids, and Intermolecular Forces
13.6K Views

11.15 : Molecular and Ionic Solids
Liquids, Solids, and Intermolecular Forces
16.6K Views
See More
Copyright © 2025 MyJoVE Corporation. All rights reserved