The half-life of a reaction (t1/2) is the time required for one-half of a given amount of reactant to be consumed. In each succeeding half-life, half of the remaining concentration of the reactant is consumed. For example, during the decomposition of hydrogen peroxide, during the first half-life (from 0.00 hours to 6.00 hours), the concentration of H2O2 decreases from 1.000 M to 0.500 M. During the second half-life (from 6.00 hours to 12.00 hours), the concentration decreases from 0.500 M to 0.250 M, while during the third half-life, it falls from 0.250 M to 0.125 M. Hence, during each successive period of 6.00 hours, the concentration of H2O2 decreases by half.
The half-life of a first-order reaction is independent of the concentration of the reactant. However, half-lives of reactions with other orders depend on the concentrations of the reactants.
Half-life of First-order Reactions
An equation relating the half-life of a first-order reaction to its rate constant may be derived from its integrated rate law:
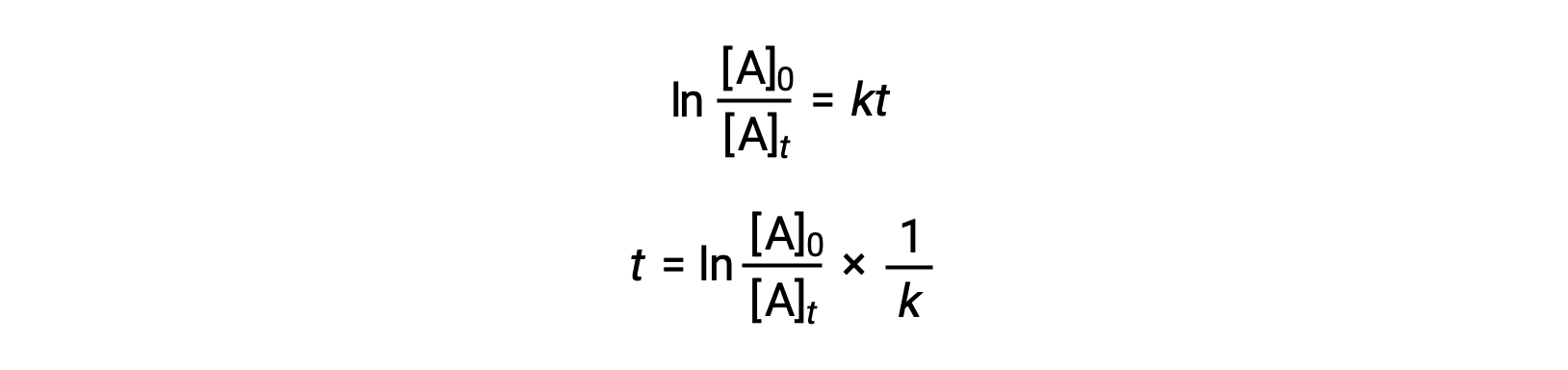
According to the definition of half-life, at time t1/2, the concentration of the reactant A is one-half of its initial concentration. Therefore; t = t1/2 and [A]t = ½ [A]0.
Substituting these terms into the rearranged integrated rate law and simplifying yields the equation for half-life:
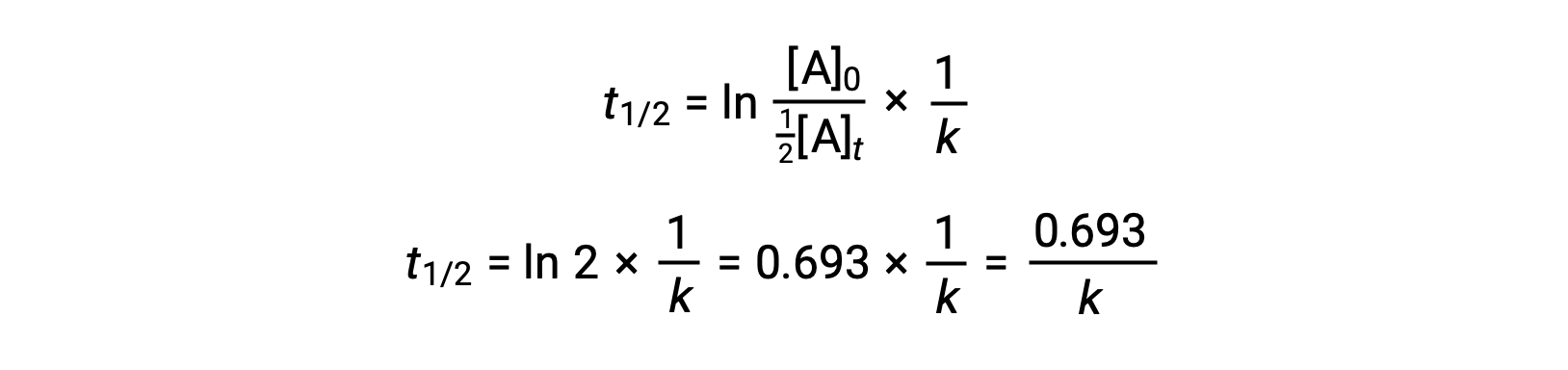
This half-life equation describes an expected inverse relationship between the half-life of the reaction and its rate constant, k. Faster reactions exhibit larger rate constants and correspondingly shorter half-lives, while slower reactions exhibit smaller rate constants and longer half-lives.
Half-life of Second-order Reactions
Following the same approach as for first-order reactions, an equation relating the half-life of a second-order reaction to its rate constant and initial concentration may be derived from its integrated rate law:
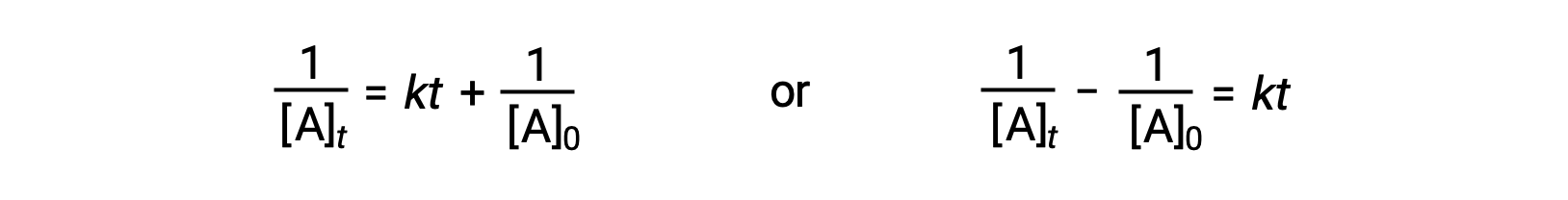
On substituting t = t1/2 and [A]t = ½[A]0, the integrated rate law is simplified:
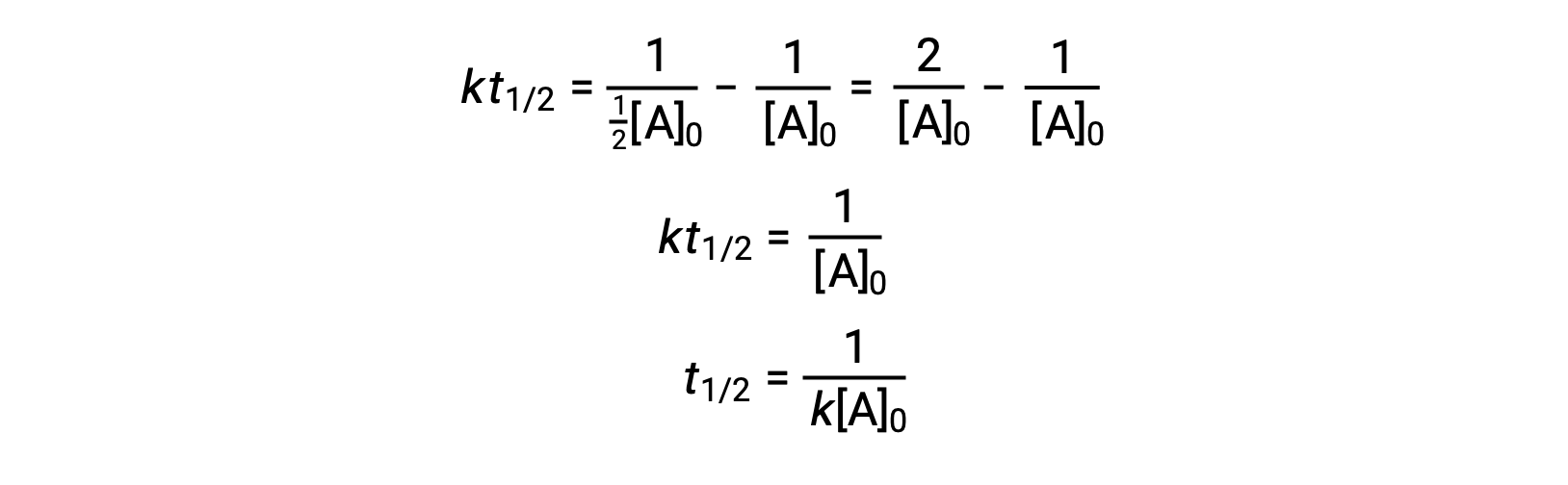
For a second-order reaction, t1/2 is inversely proportional to the concentration of the reactant, and the half-life increases as the reaction proceeds because the concentration of the reactant decreases. Unlike with first-order reactions, the rate constant of a second-order reaction cannot be calculated directly from the half-life unless the initial concentration is known.
Half-life of Zero-order Reactions
An equation for zero-order half-life may be also be derived from its integrated rate law:
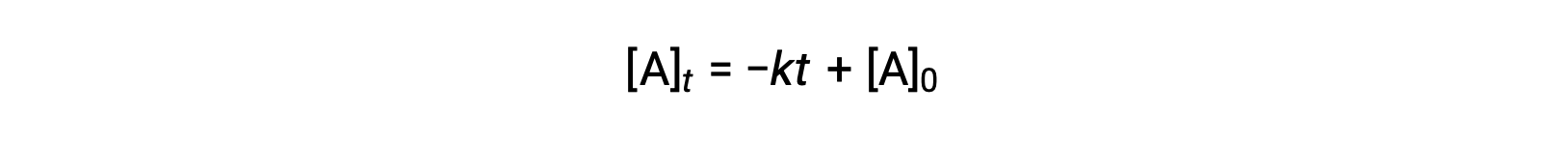
Substituting t = t1/2 and [A]t = ½ [A]0, in the zero-order integrated rate law yields:
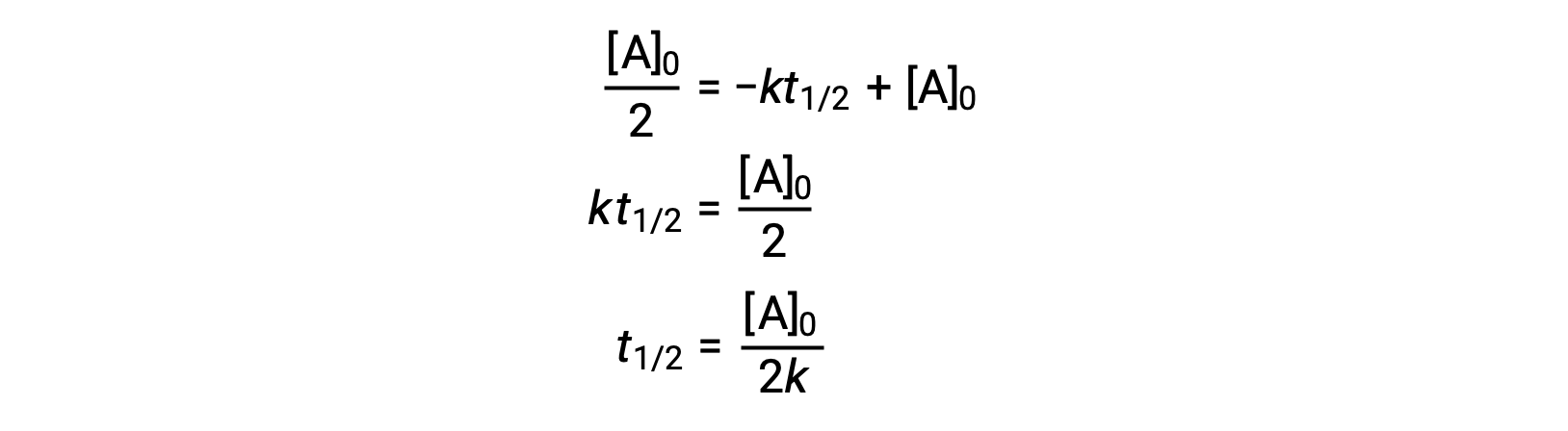
The half-life for a zero-order reaction is inversely proportional to its rate constant. However, the half-life of a zero-order reaction increases as the initial concentration increases.
This text is adapted from Openstax, Chemistry 2e, Section 12.4: Integrated Rate Laws.
ABOUT JoVE
Copyright © 2024 MyJoVE Corporation. All rights reserved