The Arrhenius equation relates the activation energy and the rate constant, k, for chemical reactions. In the Arrhenius equation, k = Ae−Ea/RT, R is the ideal gas constant, which has a value of 8.314 J/mol·K, T is the temperature on the kelvin scale, Ea is the activation energy in J/mole, e is the constant 2.7183, and A is a constant called the frequency factor, which is related to the frequency of collisions and the orientation of the reacting molecules.
The Arrhenius equation can be used to compute the activation energy of a reaction from experimental kinetic data. A convenient approach to determining the Ea for a reaction involves the measurement of k at two or more different temperatures. It uses a modified version of the Arrhenius equation that takes the form of a linear equation:
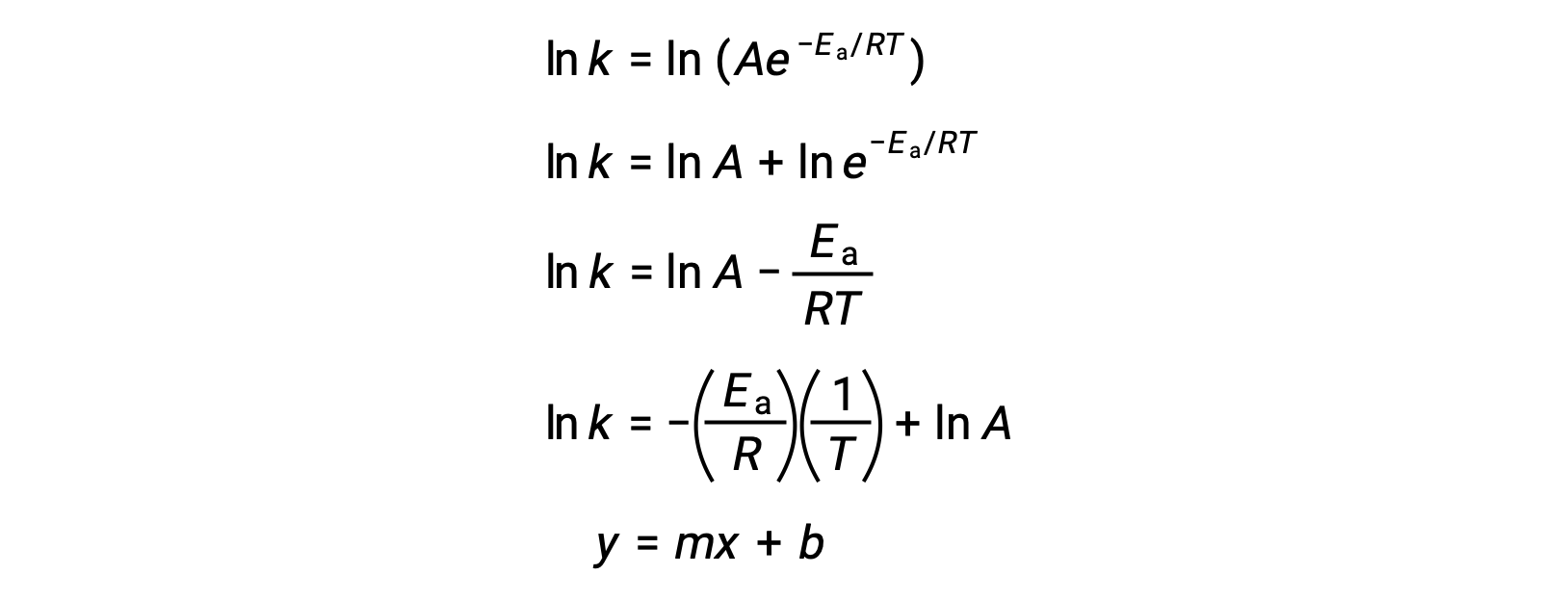
A plot of the ln k versus 1/T is linear with a slope equal to −Ea/R and y-intercept equal to ln A.
Consider the following reaction:
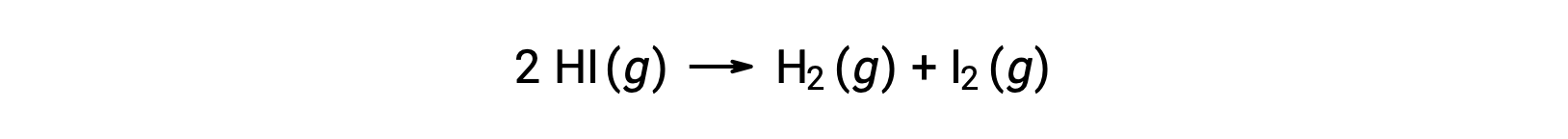
The activation energy of this reaction can be determined if the variation in the rate constant with temperature is known from the reaction kinetic data, as shown.
| Temperature (K) | Rate constant (L/mol/s) |
| 555 | 3.52 × 10–7 |
| 575 | 1.22 × 10–6 |
| 645 | 8.59 × 10–5 |
| 700 | 1.16 × 10–3 |
| 781 | 3.95× 10–2 |
The provided data can be used to derive the values of the inverse of temperature (1/T) and the natural log of k (ln k).
| 1/T (K–1) | ln k |
| 1.80 × 10–3 | –14.860 |
| 1.74 × 10–3 | –13.617 |
| 1.55 × 10–3 | –9.362 |
| 1.43 × 10–3 | –6.759 |
| 1.28 × 10–3 | –3.231 |
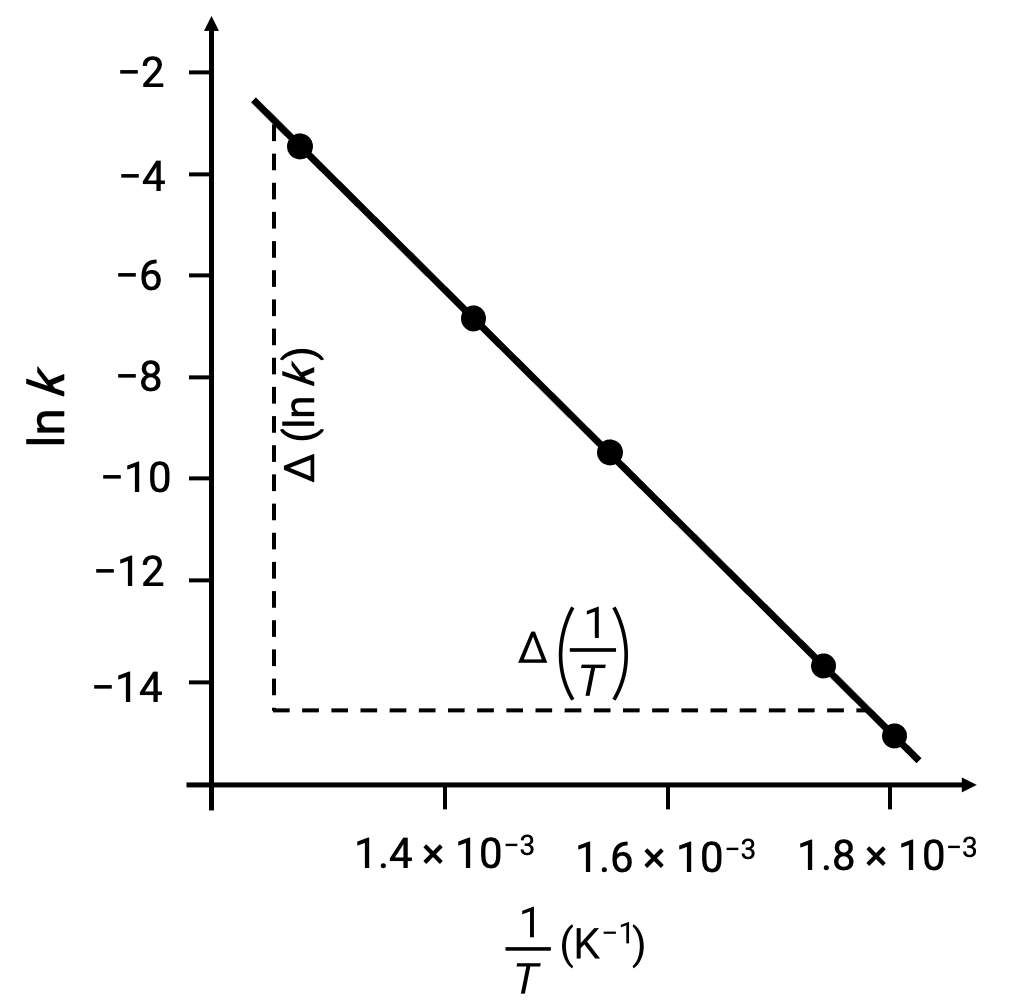
On plotting the derived data points with ln k versus 1/T, a line-graph exhibiting a linear relationship between ln k and 1/T is generated, as shown.
The slope of the line, which corresponds to the activation energy, can be estimated using any two of the experimental data pairs.

An alternative approach in deriving activation energy involves the utilization of the rate constant at two different temperatures. In this approach, the Arrhenius equation is rearranged to a convenient two-point form:
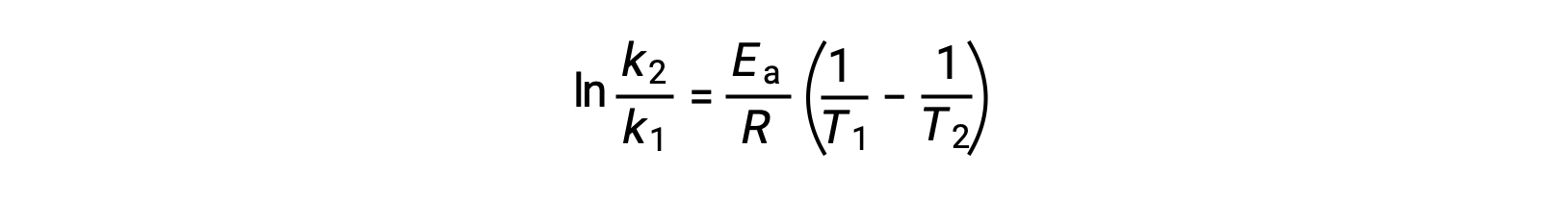
On rearranging the equation, an expression for the activation energy is generated.
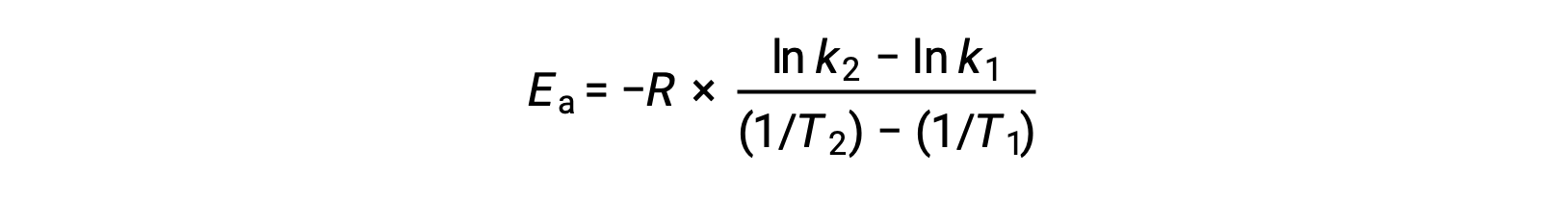
By substituting any two data pairs and further calculation yields the value for the activation energy in joules per mole or kilojoules per mole.
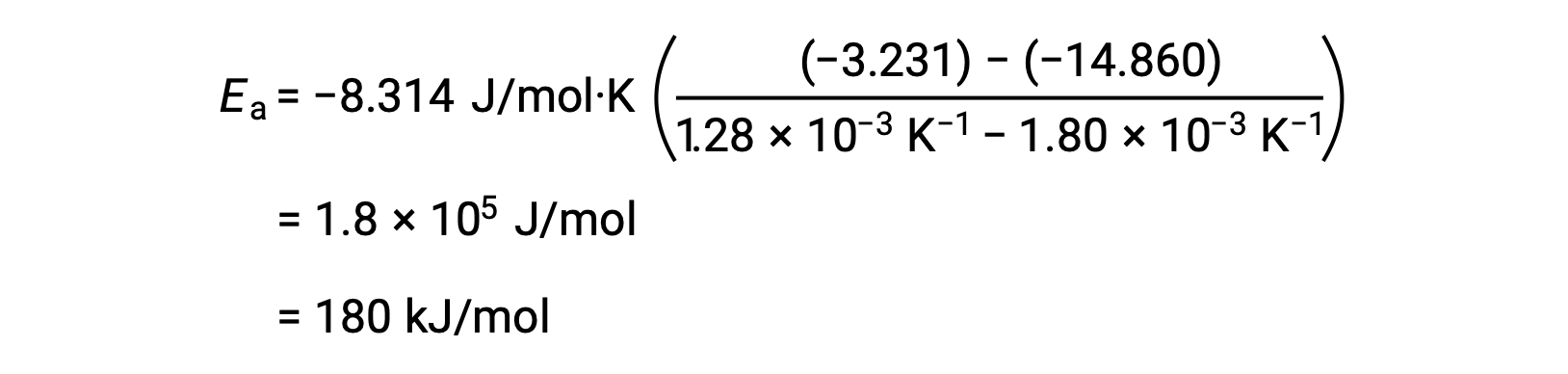
This alternative two-point approach yields the same result as the graphical approach. However, in practice, the graphical approach typically provides more reliable results while working with actual experimental data.
This text is adapted from Openstax, Chemistry 2e, Section 12.5: Collision Theory.
Tags
Aus Kapitel 13:

Now Playing
13.8 : Arrhenius Plots
Chemische Kinetik
37.0K Ansichten

13.1 : Reaktionsgeschwindigkeit
Chemische Kinetik
49.6K Ansichten

13.2 : Messung von Reaktionsgeschwindigkeiten
Chemische Kinetik
23.6K Ansichten

13.3 : Konzentrations- und Ratengesetz
Chemische Kinetik
29.0K Ansichten

13.4 : Bestimmung der Reaktionsreihenfolge
Chemische Kinetik
53.9K Ansichten

13.5 : Das integrierte Tarifgesetz: Die Abhängigkeit der Konzentration von der Zeit
Chemische Kinetik
33.3K Ansichten

13.6 : Halbwertszeit einer Reaktion
Chemische Kinetik
33.3K Ansichten

13.7 : Temperaturabhängigkeit von der Reaktionsgeschwindigkeit
Chemische Kinetik
80.1K Ansichten

13.9 : Reaktionsmechanismen
Chemische Kinetik
24.5K Ansichten

13.10 : Schritte zur Ratenbestimmung
Chemische Kinetik
30.9K Ansichten

13.11 : Katalyse
Chemische Kinetik
26.0K Ansichten

13.12 : Enzyme
Chemische Kinetik
79.7K Ansichten
Copyright © 2025 MyJoVE Corporation. Alle Rechte vorbehalten