In multiple dimensions, the conservation of momentum applies in each direction independently. Hence, to solve collisions in multiple dimensions, we should write down the momentum conservation in each direction separately. To help understand collisions in multiple dimensions, consider an example.

A small car of mass 1,200 kg traveling east at 60 km/h collides at an intersection with a truck of mass 3,000 kg traveling due north at 40 km/h. The two vehicles are locked together. What is the velocity of the combined wreckage?

Firstly, a closed system is required. The natural system to choose is the car and truck, but this system is not closed, as friction from the road acts on both vehicles. We can avoid this problem by restricting the question to finding the velocity at the instant just after the collision so that friction has not yet affected the system; thereby, momentum is conserved for this system. Since there are two directions involved, we write equations for conservation of momentum twice: once in the x-direction and once in the y-direction.

Here, the known quantities are mass of the car (m_c = 1,200 kg), mass of the truck (m_t = 3,000 kg), magnitude of velocity of the car (v_c = 60 km/h) and magnitude of velocity of the truck (v_t = 40 km/h). The magnitude of the velocity of the wreckage v_w needs to be calculated. The expression for the total momentum before the collision and after the collision is written down. Since the system is closed, the momentum must be conserved. Hence, the momentum before the collision is equal to the momentum after the collision.

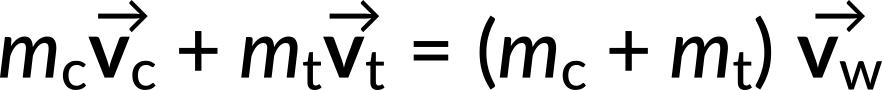
Let us define the +x-direction as pointing east and the +y-direction as pointing north. Now, the momentums are resolved along the x and y directions.

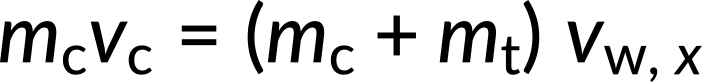
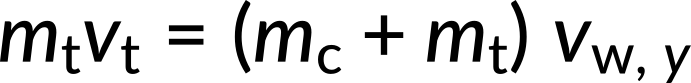
From these equations, the x and y components of the velocity of the wreckage are determined. Applying the Pythagorean theorem, the resultant velocity of the wreckage is calculated to be 33.3 km/h. The direction of velocity can be calculated using the expression,

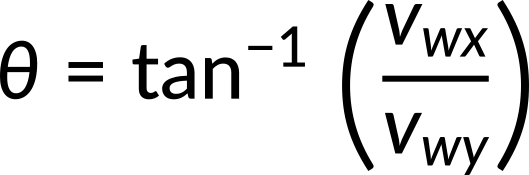
This gives the direction of velocity as 59°. This angle is towards the northeast, or 31° counterclockwise from the +x-direction.

This text is adapted from Openstax, University Physics Volume 1, Section 9.5: Collisions in Multiple Dimensions.