29.16 : Magnetostatic Boundary Conditions

An electric field suffers a discontinuity at a surface charge. Similarly, a magnetic field is discontinuous at a surface current. The perpendicular component of a magnetic field is continuous across the interface of two magnetic mediums. In contrast, its parallel component, perpendicular to the current, is discontinuous by the amount equal to the product of the vacuum permeability and the surface current. Like the scalar potential in electrostatics, the vector potential is also continuous across any boundary; hence the derivative of the vector potential is discontinuous across the boundary.

Consider two linear magnetic media with permeability μ₁ and μ₂, separated by an interface. The magnetic field intensity in medium 1 at a point P₁ has a magnitude H₁, and makes an angle α₁ with the normal. Similarly, the magnetic field intensity in medium 2 at a point P₂ has a magnitude H₂, and makes an angle α₂ with the normal.

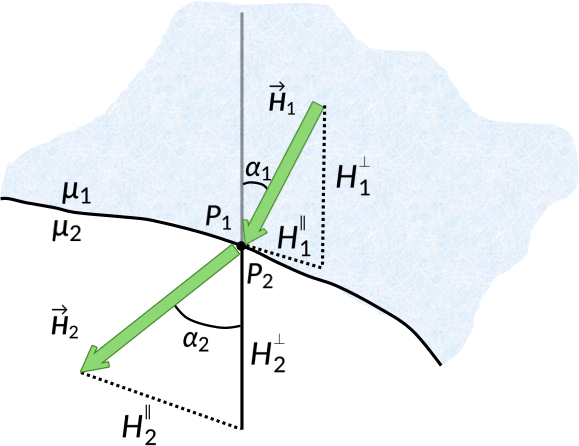
The zero divergence of the magnetic field ensures that the normal component of the magnetic field is continuous across the boundary. The magnetic field is proportional to the magnetic field intensity for linear magnetic media. Thus, the boundary conditions for the normal component of the magnetic field intensity are obtained.

Rewriting the normal components of the magnetic field in terms of the angles α₁ and α₂,

Since both media possess finite conductivities, free surface currents do not exist at the interface. Thus, the tangential component of the magnetic field intensity is continuous across the boundary. Again, the tangential components can be rewritten in terms of the angles α₁ and α₂:

Taking the ratio of normal and tangential components, a new expression is derived:

This expression is similar to the expression obtained for boundary conditions for two dielectric interfaces, except that the permittivity replaces the permeability.

If the first medium is a non-magnetic medium, like air, and the second one is a magnetic medium, the permeability of the second medium is greater than the permeability of the first medium. Thus, the angle α₂ approaches ninety degrees. This implies that, for any arbitrary angle α₁ that is not close to zero, the magnetic field in a ferromagnetic medium runs parallel to the interface. If the first medium is ferromagnetic and the second is non-magnetic, α₂ approaches zero. This implies that if a magnetic field originates in a ferromagnetic medium, the magnetic flux lines emerge into the air medium in a direction almost normal to the interface.