Name: Kinetic Energy - II
Uploaded: 2023-04-30T10:56:07
Description: Learn by watching this video about Kinetic Energy - II at JoVE.com

The kinetic energy of an object is defined as one half of the product of mass and velocity squared with the units kilograms meter squared per second squared.
The kinetic energy of an object can be calculated using the momentum equation. The velocity term in the equation can be substituted from the momentum expression. Thereby, obtaining a relationship between momentum, mass, and kinetic energy of the object.
The kinetic energy of an object depends on the frame of reference in which it is measured.
For example, consider a person sitting in a car moving at a constant velocity. Since the person is stationary, his&#160; kinetic energy with respect to another stationary person sitting in the same car is zero. While, for an observer standing outside, it is non zero.

kinetic energy - ii

The kinetic energy of a particle is one-half of the product of the particle&#8217;s mass and the square of its speed. Note that just as Newton&#8217;s second law can be expressed as either the rate of change of momentum or mass multiplied by the rate of change of velocity, so too can the kinetic energy of a particle be expressed in terms of its mass and momentum, instead of its mass and velocity.&#160;
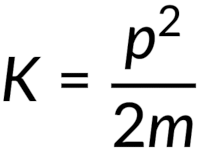
<img alt="Figure1" src="/files/ftp_upload/12667/12667_Equation_1.png" style="text-align: center; height: 35px;" />
In the equation, the units of kinetic energy are mass times the speed-squared, or
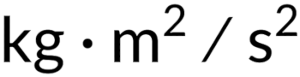
<img alt="Figure2" src="/files/ftp_upload/12667/12667_Equation_2.png" style="text-align: center; height: 20px;" />
Note that the units of force are mass multiplied by acceleration. Thus, the units of kinetic energy are also the units of force multiplied by distance, which are the units of work, or joules. Hence, work and kinetic energy have the same units, since they are different forms of the same, more general, physical property.
Because velocity is a relative quantity, the value of kinetic energy depends on the frame of reference. One can generally choose a frame of reference that is suited to the purpose of analysis and that simplifies the calculations. One such frame of reference is the one in which the observations of the system are made (likely an external frame). Another choice is a frame that is attached to or moves with the system (likely an internal frame).
This text is adapted from <a href="https://openstax.org/books/university-physics-volume-1/pages/7-2-kinetic-energy">Openstax, University Physics Volume 1, Section 7.2: Kinetic Energy.</a>

Learn by watching this video about Kinetic Energy - II at JoVE.com

Kinetic Energy - II

The kinetic energy of a particle is one-half of the product of the particle&#8217;s mass and the square of its speed. Note that just as Newton&#8217;s ...