14.4 : Gravity between Spherical Bodies
Newton's law of gravitation describes the gravitational force between any two point masses. However, for extended spherical objects like the Earth, the Moon, and other planets, the law holds with an assumption that masses of spherical objects are concentrated at their respective centers.
This assumption can be proved easily by showing that the expression for gravitational potential energy between a hollow sphere of mass (M) and a point mass (m) is the same as it would be for a pair of extended spherical solid objects.
Consider a tiny ring of width Rdϕ and mass dM on the surface of a spherical hollow sphere at a distance s from the point mass as shown in Figure 1(a).
The gravitational potential energy between the ring and the point mass (m) is expressed as:
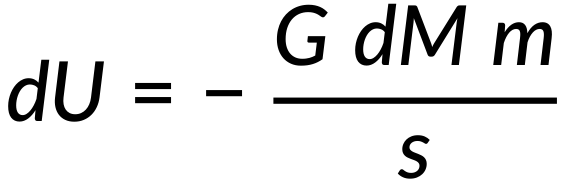
The ratio of the ring's mass to the entire shell's mass is equal to the ratio of the ring's area to the shell's area. Therefore, on simplification, the ring's mass can be expressed as:
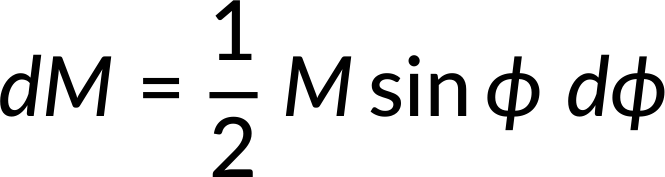
Now, the square of distance (s) can be expressed as the sum of squares of the triangle's other two sides, as seen in Figure 1(b).
Simplifying further and taking differentials on either side,
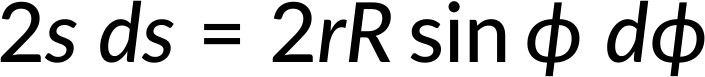
Considering the entire shell, s can vary between r − R and r + R, as seen in Figure 1(c).
Therefore, substituting dM and s in the potential energy equation and integrating within the limits of r − R to r + R, the relation obtained is the potential energy between point masses m and M at a distance r.
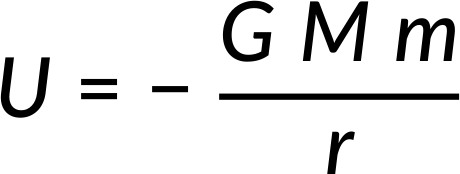
Therefore, the assumption is proven.
Since force is a derivative of potential energy, the assumption holds for gravitational forces between two spherically solid objects like the Earth and the Moon. Therefore, Newton's law of gravitation can be used to determine the gravitational force between the Earth and the Moon, and the Earth and the Sun.
From Chapter 14:

Now Playing
14.4 : Gravity between Spherical Bodies
Gravitation
7.6K Views

14.1 : Gravitation
Gravitation
5.5K Views

14.2 : Newton's Law of Gravitation
Gravitation
8.5K Views

14.3 : Gravitation Between Spherically Symmetric Masses
Gravitation
673 Views

14.5 : Reduced Mass Coordinates: Isolated Two-body Problem
Gravitation
969 Views

14.6 : Acceleration due to Gravity on Earth
Gravitation
9.8K Views

14.7 : Acceleration due to Gravity on Other Planets
Gravitation
3.9K Views

14.8 : Apparent Weight and the Earth's Rotation
Gravitation
3.4K Views

14.9 : Variation in Acceleration due to Gravity near the Earth's Surface
Gravitation
2.2K Views

14.10 : Potential Energy due to Gravitation
Gravitation
2.2K Views

14.11 : The Principle of Superposition and the Gravitational Field
Gravitation
939 Views

14.12 : Escape Velocity
Gravitation
2.0K Views

14.13 : Circular Orbits and Critical Velocity for Satellites
Gravitation
2.7K Views

14.14 : Energy of a Satellite in a Circular Orbit
Gravitation
2.0K Views

14.15 : Kepler's First Law of Planetary Motion
Gravitation
3.5K Views
See More
ABOUT JoVE
Copyright © 2025 MyJoVE Corporation. All rights reserved