5.2 : 气体定律
通过实验,科学家们建立了对理想气体保持不变的成对变量之间的数学关系,例如压力和温度,压力和体积,体积和温度以及体积和摩尔。 / p>
压力和温度:盖-呂萨克Gay-Lussac定律(阿蒙顿Amontons定律)
想象一下,用气体填充连接到压力表的刚性容器,然后密封该容器,以免气体逸出。如果容器被冷却,内部气体同样变冷,并且观察到其压力降低。由于容器是刚性且紧密密封的,因此气体的体积和摩尔数均保持恒定。如果球体被加热,内部的气体就会变热,压力也会增加。
温度和压力成线性关系,对于任何限制在恒定体积内的气体样品,都可以观察到这种关系。如果温度在开尔文尺度上,则 P 和 T 成正比(同样,当气体的体积和摩尔数保持恒定时);如果开尔文标度上的温度升高一定倍数,气压将增加相同倍数。
这种气体的压力-温度关系被称为盖-吕萨克定律。该法则规定,当体积保持恒定时,给定数量的气体的压力与开尔文刻度上的温度成正比。从数学上讲,可以这样写:
其中 k 是比例常数,取决于气体的特性,量和体积。因此,对于有限的恒定气体体积, P / T 之比是恒定的(即, P / T > = k )。如果气体最初处于"状态1"状态, (其中 P = P 1 和 T = T 1 < / sub>),然后更改为"条件2" (其中 P = P 2 和 T = T 2 < / sub>),然后
因此&nbsp;
请注意,对于任何气体定律计算,温度必须在开尔文刻度上。
如果气球充满空气并被密封,则该气球在大气压(1个大气压)下包含特定量的空气。如果将气球放在冰箱中,则内部气体会变冷,并且气球会收缩(尽管气体量及其压力均保持恒定)。如果将气球制成很冷,它将收缩很多。预热后,气球将再次膨胀。
这是在恒定压力下温度对一定量的受限气体体积影响的一个例子。体积随温度升高而增加,体积随温度降低而减小。
在恒定压力下给定数量的气体的体积和温度之间的关系被称为查尔斯定律。该法则规定,当压力保持恒定时,给定气体量与开尔文尺度上的温度成正比。
从数学上讲,可以这样写:
其中 k 是一个比例常数,取决于气体的量和压力。对于恒定压力下的受限气体, V / T 之比是恒定的。
减少所含气体的体积将增加其压力,而增加其体积将降低其压力。如果体积增加某个系数,则压力降低相同的系数,反之亦然。因此,压力和体积呈反比例关系:比例:增加压力会导致气体体积减少。数学上可以这样写:
其中 k 是一个常数。 P 与 V 的曲线图显示了一个双曲线。带有曲线的图形很难在变量的低值或高值下准确读取,并且更难以用于将理论方程式和参数拟合到实验数据中。由于这些原因,科学家经常尝试寻找一种方法来"线性化"他们的数据。以图形方式显示压力与体积之间的关系,方法是绘制压力与体积的倒数,或者体积与压力的倒数。
恒定温度下给定数量的气体的体积与压力之间的关系由波义耳定律给出:恒定温度下给定数量的气体的体积与测量时的压力成反比
意大利科学家阿梅代奥·阿伏伽德罗(Amedeo Avogadro)于1811年提出了一种假说,以解释气体的行为,并指出,在相同的温度和压力条件下测量的所有体积相等的气体包含相同数量的分子。随着时间的流逝,这种关系得到了阿伏伽德罗定律表示的许多实验观察的支持:对于承压气体,如果压力和温度都保持恒定,则体积(V)和摩尔数(n)成正比。 / p>
以等式形式表示为:
还可以确定其他变量对的数学关系,例如 P 与 n 和 n 与 T < / em>。
将这四个定律结合起来,就可以得出理想的气体定律,即气体的压力,体积,温度和摩尔数之间的关系:
在这里, R 是一个常数,称为理想气体常数或通用气体常数。用于表示压力,体积和温度的单位决定了尺寸分析所需的气体常数的适当形式。 R中最常遇到的值为0.08206 L·atm mol &lt; 1 &sdot; K &ndash; 1 和8.314 kPa·L mol &ndash; 1 &sdot; K &ndash; 1 。
通过理想气体定律(或其他气体定律)准确描述 P , V 和 T 的气体是据说表现出理想的行为或近似于理想气体的特性。理想气体是仅在相对低压和高温条件下才对气体合理的假想构造。
理想气体方程包含五个项,气体常数 R 和变量属性 P , V , n 和 T 。指定这些术语中的任何四个,将允许使用理想气体定律来计算第五个术语。
如果理想气体的摩尔数在两组不同的条件下保持恒定,则将获得一个有用的数学关系,称为组合气体定律(使用atm,L和K的单位):
两组条件均等于 n &times;的乘积。 R (其中 n =气体的摩尔数, R 是理想的气体定律常数)。

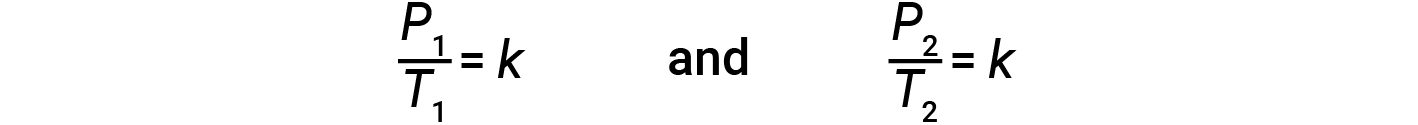
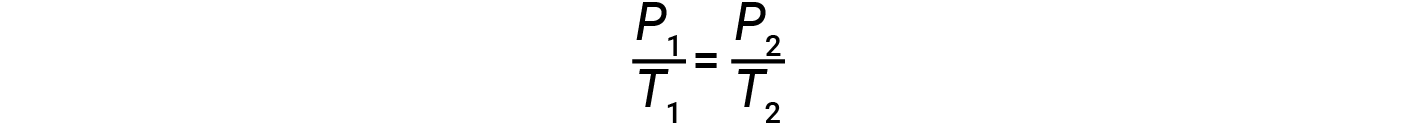
体积和温度:查尔斯定律
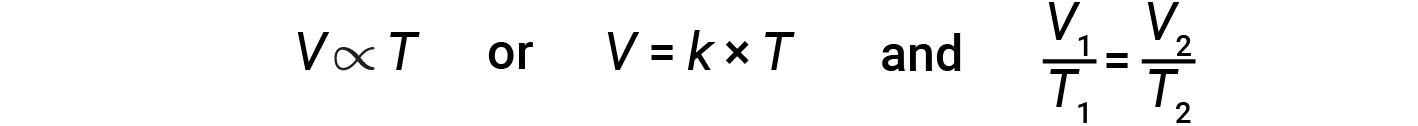
体积和压力:波义耳定律
如果气密的注射器部分充满空气,则该注射器在恒定温度(例如25℃)下包含特定量的空气。如果在温度保持恒定的状态下缓慢按压柱塞,则注射器中的气体被压缩为较小的体积,并且其压力会升高。如果抽出柱塞,则气体量会增加,压力会降低。
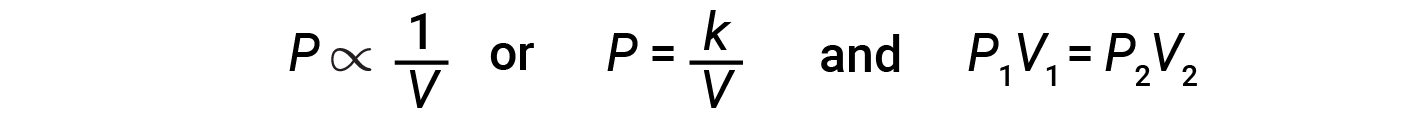
气体和体积摩尔:阿伏伽德罗定律
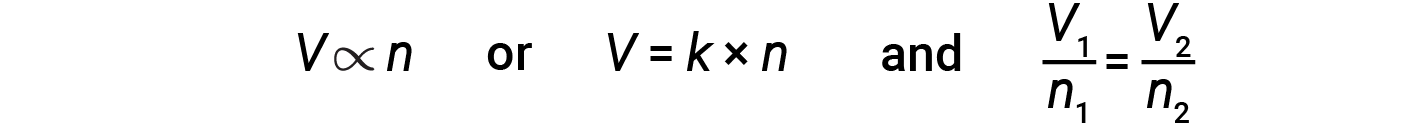
理想气体定律
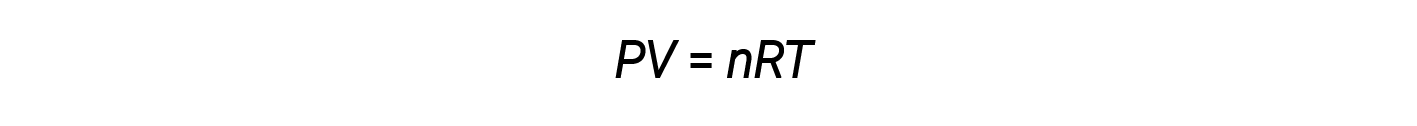
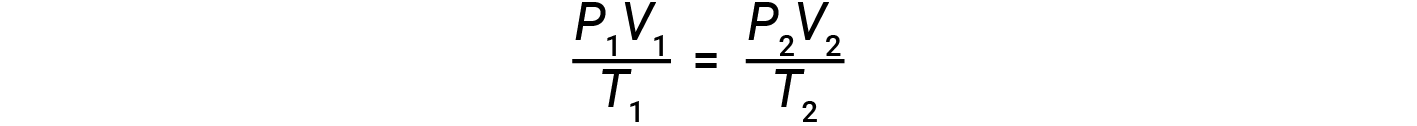
来自章节 5:

Now Playing
5.2 : 气体定律
热化学
65.7K Views

5.1 : 压力和测量压力
热化学
35.7K Views

5.3 : 理想气体定律的应用:摩尔质量、密度和体积
热化学
56.2K Views

5.4 : 气体混合物-道尔顿分压定律
热化学
38.9K Views

5.5 : 化学计量学和气体
热化学
24.4K Views

5.6 : 动力学分子理论:基本假设
热化学
33.6K Views

5.7 : 动力学分子理论与气体定律
热化学
32.4K Views

5.8 : 分子速度和动能
热化学
27.3K Views

5.9 : 渗出和扩散
热化学
28.5K Views

5.10 : 真实气体-偏离理想气体定律
热化学
34.4K Views
版权所属 © 2025 MyJoVE 公司版权所有,本公司不涉及任何医疗业务和医疗服务。