7.7 : 德布罗意波长
在宏观世界中,足够大以肉眼可见的物体遵循经典物理学的规则。在桌子上移动的台球的行为就像颗粒。它会继续沿直线行进,除非它与另一个球碰撞,或者受到其他一些力(例如摩擦力)的作用。球具有明确定义的位置和速度或明确定义的动量, p = mv ,由质量 m 和速度< em> v 在任何给定的时刻。这是经典对象的典型行为。
当波彼此相互作用时,它们会显示出干涉图案,这些图案不会被宏观粒子(如撞球)显示出来。然而,到了1920年代,越来越明显的是,很小的物质遵循与大物体不同的一组规则。在微观世界中,波和粒子是密不可分的。
路易斯·德·布罗意(Louis de Broglie)是最早关注微观世界特殊行为的人之一。他质疑电磁辐射是否可以具有粒子状的特性,电子和其他亚微观粒子是否可以表现出波状的特性?德布罗意(De Broglie)扩展了爱因斯坦用来将光电效应悖论解析为物质粒子的光的波粒二象性。他预测质量为m且速度为 v (即线性动量为 p )的质点也应表现出波长为λ的波的行为。通过以下表达式,其中 h 是普朗克常数:
这称为德布罗意波长。玻尔将电子假定为在量子轨道上绕原子核运行的粒子的地方,德布罗意认为,如果将电子视为圆驻波,则可以解释玻尔对量子的假设。只有整数个波长才能完全适合该轨道。
如果将电子看作是绕原子核盘旋的波,则必须使整数个波长适合轨道,才能使这种驻波行为成为可能。
对于半径为r的圆形轨道,周长为2π r ,因此德布罗意的条件为:
其中 n = 1、2、3,依此类推。在德布罗意提出物质的波性质后不久,贝尔实验室的两位科学家戴维森(C. J. Davisson)和杰默(L. H. Germer)通过实验证明了电子可以表现出波状行为。通过将电子束对准晶体镍靶来证明这一点。晶格内原子的间距与瞄准它的电子的德布罗意波长大致相同,晶体的规则间隔原子层用作"狭缝"。用于其他干扰实验。
最初,当仅记录几个电子时,观察到清晰的颗粒状行为。随着越来越多的电子到达并被记录,清晰的干涉图样出现了,这是波状行为的标志。因此,看来,尽管电子是小的局部粒子,但它们的运动却不遵循经典力学所隐含的运动方程。相反,它们的运动由波动方程控制。因此,首先用光子观察到的波粒二象性是所有量子粒子固有的基本行为。
本文改编自 Openstax,化学 2e,第6.3节:量子理论的发展。 
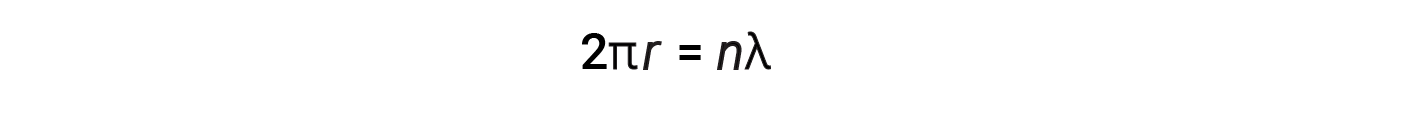
来自章节 7:

Now Playing
7.7 : 德布罗意波长
元素的周期律
25.3K Views

7.1 : 光的波动本质
元素的周期律
48.4K Views

7.2 : 电磁频谱
元素的周期律
52.6K Views

7.3 : 干涉和衍射
元素的周期律
32.0K Views

7.4 : 光电效应
元素的周期律
29.4K Views

7.5 : 玻尔模型
元素的周期律
51.4K Views

7.6 : 发射光谱
元素的周期律
51.0K Views

7.8 : 不确定性原则
元素的周期律
23.1K Views

7.9 : 原子的量子力学模型
元素的周期律
42.0K Views

7.10 : 量子数
元素的周期律
34.4K Views

7.11 : 原子轨道
元素的周期律
33.2K Views

7.12 : 保利排除原则(PEP)亦称:泡利不相容原理
元素的周期律
35.4K Views

7.13 : 原子轨道的能量
元素的周期律
23.8K Views

7.14 : 构造原理与洪德规则
元素的周期律
46.6K Views

7.15 : 多电子原子的电子构型
元素的周期律
39.3K Views
版权所属 © 2025 MyJoVE 公司版权所有,本公司不涉及任何医疗业务和医疗服务。