24.6 : Calculations of Electric Potential I
Consider a ring of radius R with a uniform charge density λ. What will the electric potential be at point M, which is located on the axis of the ring at a distance x from the center of the ring?
The ring is divided into infinitesimal small arcs such that point M is equidistant from all the arcs. Here, the cylindrical coordinate system is used to calculate the electric potential at point M. A general element of the arc between anglesθand θ + dθis of the length Rdθand has a charge of λRdθ.
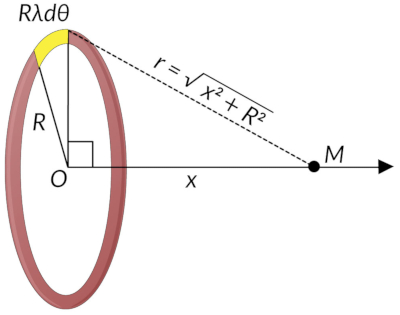
The distance between this element of the ring and the point M is
The potential at point M due to the charge on the whole ring is
Integrating the above equation over the limits gives,
Here, 2πRλ accounts for the whole charge on the ring; therefore, the above equation can be written as
This result is expected because point M is equidistant from all the infinitesimal ring elements, and the total potential will be similar to if the total charge were positioned at a common distance from point M.
来自章节 24:

Now Playing
24.6 : Calculations of Electric Potential I
Electric Potential
1.9K Views

24.1 : 电势能
Electric Potential
5.6K Views

24.2 : 均匀电场中的电势能
Electric Potential
4.5K Views

24.3 : 两点电荷的势能
Electric Potential
4.4K Views

24.4 : 电位和电位差
Electric Potential
4.3K Views

24.5 : 从电场中寻找电势
Electric Potential
4.0K Views

24.7 : 电势计算 II
Electric Potential
1.6K Views

24.8 : 等势面和磁力线
Electric Potential
3.6K Views

24.9 : 等电位表面和导体
Electric Potential
3.3K Views

24.10 : 根据电势确定电场
Electric Potential
4.3K Views

24.11 : 泊松和拉普拉斯方程
Electric Potential
2.5K Views

24.12 : Van de Graaff 生成器
Electric Potential
1.6K Views

24.13 : 与电荷分布相关的能量
Electric Potential
1.5K Views

24.14 : 静电边界条件
Electric Potential
394 Views

24.15 : 第二唯一性定理
Electric Potential
951 Views
版权所属 © 2025 MyJoVE 公司版权所有,本公司不涉及任何医疗业务和医疗服务。