Consider a ring of radius R with a uniform charge density λ. What will the electric potential be at point M, which is located on the axis of the ring at a distance x from the center of the ring?
The ring is divided into infinitesimal small arcs such that point M is equidistant from all the arcs. Here, the cylindrical coordinate system is used to calculate the electric potential at point M. A general element of the arc between anglesθand θ + dθis of the length Rdθand has a charge of λRdθ.
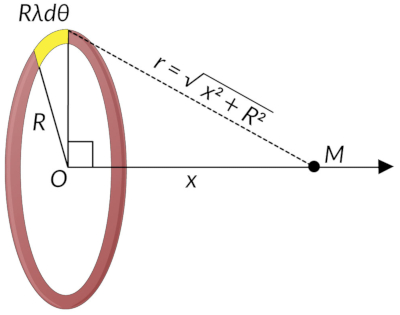
The distance between this element of the ring and the point M is
The potential at point M due to the charge on the whole ring is
Integrating the above equation over the limits gives,
Here, 2πRλ accounts for the whole charge on the ring; therefore, the above equation can be written as
This result is expected because point M is equidistant from all the infinitesimal ring elements, and the total potential will be similar to if the total charge were positioned at a common distance from point M.
Aus Kapitel 24:

Now Playing
24.6 : Calculations of Electric Potential I
Electric Potential
1.8K Ansichten

24.1 : Elektrische potentielle Energie
Electric Potential
5.2K Ansichten

24.2 : Potentielle elektrische Energie in einem gleichmäßigen elektrischen Feld
Electric Potential
4.3K Ansichten

24.3 : Potentielle elektrische Energie von Zweipunktladungen
Electric Potential
4.2K Ansichten

24.4 : Elektrisches Potential und Potentialdifferenz
Electric Potential
4.1K Ansichten

24.5 : Auffinden des elektrischen Potentials aus dem elektrischen Feld
Electric Potential
3.8K Ansichten

24.7 : Berechnungen des elektrischen Potentials II
Electric Potential
1.5K Ansichten

24.8 : Potentialäquipotentialflächen und Feldlinien
Electric Potential
3.5K Ansichten

24.9 : Potentialausgleichsflächen und Leiter
Electric Potential
3.2K Ansichten

24.10 : Bestimmung des elektrischen Feldes aus dem elektrischen Potential
Electric Potential
4.3K Ansichten

24.11 : Poisson- und Laplace-Gleichung
Electric Potential
2.4K Ansichten

24.12 : Van-de-Graaff-Generator
Electric Potential
1.6K Ansichten

24.13 : Energie, die mit einer Ladungsverteilung verbunden ist
Electric Potential
1.4K Ansichten

24.14 : Elektrostatische Randbedingungen
Electric Potential
356 Ansichten

24.15 : Zweiter Einzigartigkeitssatz
Electric Potential
918 Ansichten
Copyright © 2025 MyJoVE Corporation. Alle Rechte vorbehalten