脑电图神经影像数据：事件相关电位，光谱功率，和多尺度熵的应用

摘要

神经影像学研究人员通常认为大脑的反应平均活动跨越反复试验和无视“噪音”信号的变化随着时间的推移。然而，这是越来越明显，有信号，噪声。本文介绍了新方法的多尺度熵量化大脑信号在时域的变化。

摘要

当考虑人类神经影像数据信号的可变性，升值是一个根本性的创新，我们的思维方式有关的大脑信号。通常情况下，研究人员表示大脑的反应平均跨越反复试验和，无视信号波动，随着时间的推移，“噪音”。然而，这是越来越明显，大脑信号变异神经网络的动态信息传达有意义的功能。本文介绍了一种新方法进行量化脑信号变化的多尺度熵（MSE）。 MSE可能是特别的信息，因为它显示时间刻度的依赖性和灵敏度数据中的线性和非线性动态神经网络动力学。

引言

神经影像学的最新进展已经大大充实了我们的大脑功能的理解。然而，许多神经影像数据的应用往往比强调认知操作，因为他们实时地在加强静态的状态，而大脑的看法。因此，仅很少知道关于脑网络结构和空间 - 时间序列的变化，在多个时间尺度上的时空模式纳入到一个特定的认知操作。本文章介绍了多尺度熵^{（MSE）5，}神经影像学检查数据的时空格局的复杂性，相关的特定的认知操作提供的信息如何在大脑功能性网络通信在多个时间尺度不同的神经发电机的一个新的分析工具。

来自信息理论，应用数学分支^7,16，MSE是原LY旨在探讨复杂的心电图^4。从理论上讲，MSE可以用于分析任何时间序列的复杂性，初级所需的信号的时间序列，包含至少50个数据点的持续时间。然而，在数据的线性和非线性动力学的时间尺度依赖性和敏感性可能使MSE特别神经网络的动态信息。

在这里，我们重点MSE应用脑电图（EEG）神经影像数据^9,12。 EEG是一种非侵入性神经影像技术，通过该技术被放置在头皮上的电极捕捉¹新皮层神经元种群的突触后反应。具有高时间分辨率，脑电图没有改变典型的收购协议，轻松满足必要的MSE时间序列长度。要强调的效用MSE脑电图数据的应用中，我们比较这种新方法与传统的方法，包括UDING事件相关电位和功率谱。当一起使用时，这些互补性的分析方法的数据，可能会导致进一步洞察产生认知的神经网络运营提供更完整的说明。

研究方案

1。脑电信号采集

1. 将解释实验程序的参与者，并取得知情同意。
2. 应用下拉电极。洁净区下拉电极使用酒精棉签将设在脸上。
3. 对参与者的头部放置电极帽。测量参与者的头围，并选择适当的上限大小。按照国际公认的10-20系统放置电极，测量距离从鼻根点至INION，沿中线划分了10％。使用这一数字，测量，从鼻根和标记。对准电极帽有这种标志的位置FP和回拉帽。请确保该中心的上限是用鼻子一致。测量鼻根点至CZ，并确认这个距离从鼻根点至INION的距离的一半。拧紧帽带。
4. 将凝胶填充注射器在电极持有人钝点。要创建一个导电柱凝胶，开始接触在头皮上，再挤拉了回来。需要注意的是过多的凝胶的应用可以桥接相邻的电极的信号。
5. 修复活性电极插入电极持有人。
6. 被摄物体定位在显示器前面的实验的合适的距离。要求参与者保持不动，强调尽量减少眼球运动和一个干净的录音闪烁的重要性。
7. 检查电极连接和脑电图信号质量的收购计算机上。验证所有电极偏移量低（<40毫伏）和稳定。如果存在的问题，特别是电极，在该电极，并重新应用凝胶在该站点来调整阻抗。
8. 保存文件并开始实验。

2。脑电图分析

1. 经过实验，但在此之前提取的特殊利益统计，预处理不间断的脑电数据删除使用标准程序过滤一个文物第二神器抑制。切连续脑电图成时代对应到每一个离散事件，如照片的演示。在每个时代，包括一个100毫秒的预刺激窗口作为基准。
2. 事件相关电位（ERP）的分析捕获同步的大脑活动的相位锁定到该事件的发病。各试验平均分开诱发反应的“噪音”（ 即非锁相）背景活动。各试验受试者间的变异介绍ERP的分析方法的一大挑战。要实现良好的信号噪声比实验的协议应包括许多可定义声母的离散事件。锁定大脑的反应的一个显着的事件的发生，然后平均超过许多类似事件的时间，可以减少一些这种噪声，但是，在此过程的时间同步性典型地在1秒内溶解。确定ERP组件峰值振幅和潜伏期为每个子拍摄对象（ERP分析更详细的指引，看到皮克顿等人，2000）。
3. 使用傅立叶分析，EEG信号从时域变换到频域的信号分解成不同的频率⁶的复合正弦波。
4. 多尺度熵（MSE）是一个信息理论度量，估计随着时间的推移，在多个时间尺度的变异性的neuroelectical信号。提供一种概念描绘的MSE的分析，考虑两个模拟波形，有规律的波形和更随机的。对于常规波形样本熵值接近零，〜2.5可变波形。样本熵的增加对应于信号的复杂性的增加，其中，根据信息理论，可以解释为增加量的信息处理能力的底层系统^7,16。请记住，脑的容量是不固定的，但更改DEPEnding神经上下文^2， 即大脑区域，发生在一个特定的时间点的功能连接。
5. 来计算的均方误差，使用该算法可在www.physionet.org/physiotools/mse/ ，在两个步骤中计算的MSE。
6. 首先，算法逐渐下降脑电时间序列样本每试验和每个条件。下样品的原始时间序列生成多个不同时间尺度的时间序列。时间系列1是原始时间序列。要创建的时间序列中随后的时间尺度，原来的时间序列分割为不重叠的时间刻度的长度，平均窗口在每个窗口内的数据点。下采样是类似的低通滤波;时间刻度除以采样频率近似的频率的信号，低通滤波，在该特定的时间。 MSE相提并论的应用满足特殊的频率范围（ 例如 ，比旋光度：9赫兹到12赫兹），可以被解释为代表的组合物，在该范围内的节奏，以及在这些频率之间的相互作用。
7. 其次，算法计算每一个粗粒度的时间序列¹⁴的样本熵。样本熵估计的时间序列的复杂性。在脑电图的非线性分析，假设，一个人的时间序列代表一个潜在的多维非线性动态模型（见斯塔姆，2005年进行检讨）的表现。在这个例子中，模式的长度（米）被设置为2，表示在二维与三维空间中，通过考虑两个对三个连续的顺序模式的振幅模式的每个时间序列的变异性将被表示数据点分别。参数r（相似准则），反映了幅度范围（由彩色带的高度表示）内的数据点重新考虑“匹配”。对于一个典型的脑电时间序列超过100个数据点，设置参数m等于2，参数r等于0.5和1之间的值（见里奇曼和穆尔曼，2000;上选择参数的详细步骤，请参阅湖等 ，2002）。
   要计算这个模拟的时间序列样本熵，开始与第一双组分的序列模式，橘红色。首先，橘红色的序列模式在时间序列中出现的次数，数一数，有10场比赛，这两个组件序列。其次，算上倍前三组件序列模式的数量，红 - 橙 - 黄，在时间序列中出现，有5场比赛，这三个组件序列。继续接下来的两个组件序列（橙黄色）相同的操作和下三分量序列（橙，黄，绿）的时间序列。双组分相匹配（5）和三分量匹配（3）的数量的这些sequen加以添加到以前的值（总的双组分匹配= 15;三种成分的总的条件= 8）。重复比赛时间序列中的所有其他序列（N - M）双组分三组分匹配匹配确定的总比例。样本熵是这个比例的自然对数。对于每一个主题，计算特定通道MSE估计每个时间表两端的平均单试用熵措施。

结果

图1A和2A代表的EEG信号响应人脸图像演示。平均对面像试验产生了一系列的正面和负面的挠度称为ERP成分组成的ERP波形图1B说明一个主题， 图6A说明了盛大的平均波形为一组受试者的平均波形。有丰富的文献，涉及每个ERP组件特定的感性，电机，操作或认知。例如，N170是一种消极的偏转，在约170毫秒的刺激后发病高峰，并牵连面处理^8,15。

图2B示出了该相同的EEG信号到分量频带的分解。从功率谱分析的结果揭示了的频率成分的信号（ 图2C），从而在一个特定的频率上的功率的增加反映内的EEG信号的存在下，节奏增加。

喜欢频谱功率，MSE是敏感的贡献该信号的振荡元件的复杂性。然而，不像频谱功率，MSE也是敏感的频率分量（ 即非线性动力学^18）之间的相互作用。 EEG信号的复杂性来表示的样本熵（ 图5）为一个函数，在多个时间尺度（ 图4）。正如图3中所示，样本熵是低的的定期信号和随信号的随机性的程度。不同于传统的熵措施随机性程度的增加，多尺度熵是考虑到跨越多个时间尺度熵能够区分复杂的白噪声信号。例如，哥斯达黎加等，比2005年多尺度熵值f或不相关的相关噪声与噪声（粉红色）（白色）。虽然样本熵精细尺度更大的为白噪音比粉红噪声，相反的观察在时间尺度粗糙5-20。换句话说，当熵被认为是在多个时间尺度上，真正的复杂的信号更准确的表达比将被认为，如果只有一个单一的时间刻度。条件的影响根据一个特定的时间动态的对比度，可表示为：1）以同样的方式在所有的时间尺度，2）在某些时间尺度，但没有其他，或3）作为交叉效应，从而对比度不同的细与粗时间表。

图6描述了在ERP条件的差异（ 图6A），功率谱（ 图6B），MSE（图6C）对比初始与重复演示正面照片^9。在这个例子中，所有措施的融合揭示同样的效果，但是，所观察到的样本熵的减少，伴随着脸上重复是很重要的，因为它限制了对结果的解释。减少复杂性表明，底层的网络功能比较简单，能够处理的信息较少。

图7显示了多元统计结果分析，偏最小二乘¹¹适用于ERP，功率谱和MSE。实验操作的熟悉与不同的面孔（Heisz， 等人，2012）。对比度（条形图）显示，ERP振幅区分新的面孔，熟悉的面孔，但不属于熟悉的面孔不同之前曝光量的。光谱功率区分面临根据获得的熟悉，但没有准确区分中，低熟悉的面孔。 MSE是最敏感的条件差异，样本熵值越来越与脸熟增加。影像显示捕获的时空分布电极在所有条件下的效果和时间/频率/时间表。这个例子演示了一种情况，即脑电图分析MSE制作独特的信息，并没有使用传统ERP或功率谱的方法获得。这种分歧的MSE表明自己的网络动态非线性方面的条件不同，可能涉及各种频率成分之间的相互作用。

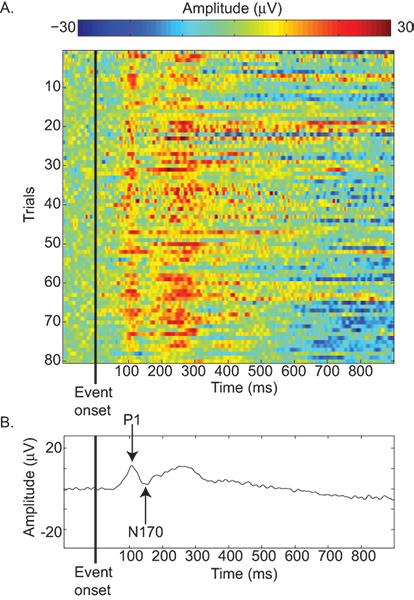
图1）脑电图偏转幅度从每次试验的基线作为一个功能单一主体的响应时间绘制从发病的审判。每个试验包括了人脸图像的照片演示。正幅度挠度中描绘了红色，用蓝色表示负振幅偏转。所有试验均表现出积极的偏转大约100毫秒，250毫秒，指示与事件相关的相位锁定的活动。 乙）在图1A中示出在所有试验中平均产生一个平均的ERP波形具有鲜明的正面和负面的偏转被称为事件相关的组件和命名根据一个标准的命名法。例如，P1是第一正打算组成部分，N170是一种消极的成分，在约170毫秒的刺激后发病高峰。

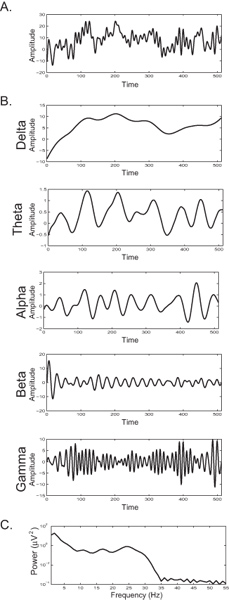
图2：A）一个单一的主题绘图幅度审单时间（数据点，采样率为512赫兹）B）脑电图反应图2A通过滤隔离频段三角洲脑电图反应描绘在图 （0-4赫兹），θ（5-8赫兹），α（9-12赫兹），β（13-30赫兹）和γ（> 30赫兹）。C）的谱功率密度的EEG响应2A表示作为频率的函数的功率信号的频率组成。光谱功率的增加反映了在某一特定频率，特定频带内夹带的同步活跃的神经元的数量增加。 点击这里查看大图 。

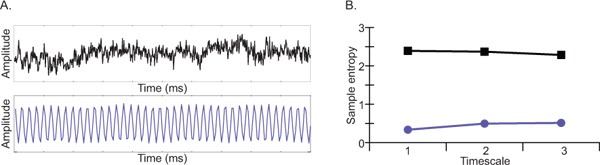
图3）两个模拟波形：定期或可预见的紫色描绘的波形，更随机的波形描绘黑色B）两个模拟波形样本熵值前三的时间表。样品ENTR冠层低高度可预测的随机信号的信号比。 点击这里查看大图 。

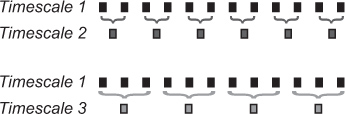
图4。降采样原始时间序列生成多个不同时间尺度的时间序列，时间刻度1是原始时间序列。创建时间刻度2的时间序列除以原始时间序列的非重叠的长度为2和平均每个窗口内的数据点的窗口。要生成的时间序列中随后的时间尺度，原来的时间序列分割为不重叠的时间刻度的长度，平均窗口在每个窗口内的数据点。

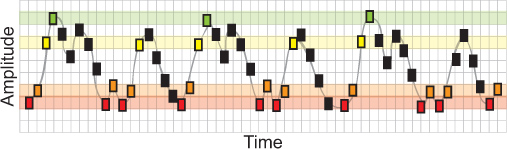
图5。其中每个矩形代表一个单独的数据点在时间序列中。样本熵的模拟波形估计时间序列的变异。在这个例子中，模式的长度（ 米 ）被设置为2，表示在二维与三维空间中，通过考虑两个对三个连续的顺序模式，将表示每个时间序列的振幅模式的方差数据点，分别为r（下相似准则），反映了幅度范围（由彩色带的高度表示）内的数据点被认为是“匹配”。要计算这个模拟的时间序列样本熵，开始与第一双组分的序列模式，橘红色。首先，橘红色的序列模式在时间序列中出现的次数，数一数，有10场比赛，这两个组件序列。二，算多少倍前三的组件序列模式，橘红色声援OW，发生在时间序列中，有5场比赛，这三个组件序列。以这种方式继续接下来的两个组件序列（橙黄色）和三分量序列（橙，黄，绿）。双组分匹配（5）和三分量匹配（3）对这些序列的数目被添加到先前的值（总的双组分匹配= 15;三种成分的总的条件= 8）。重复比赛时间序列中的所有其他序列（N - M）双组分三组分匹配匹配确定的总比例。样本熵是这个比例的自然对数。对于每一个主题，计算特定通道MSE估计每个时间表两端的平均单试用熵措施。

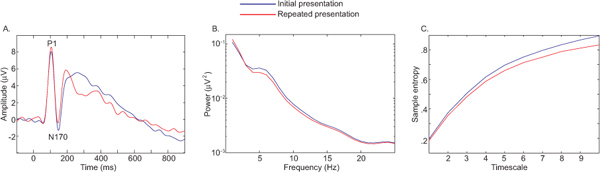
图6。在ERP条件的差异，功率谱（B），（A）MSE（C）对比首次与反复的介绍面部照片。 点击这里查看大图 。

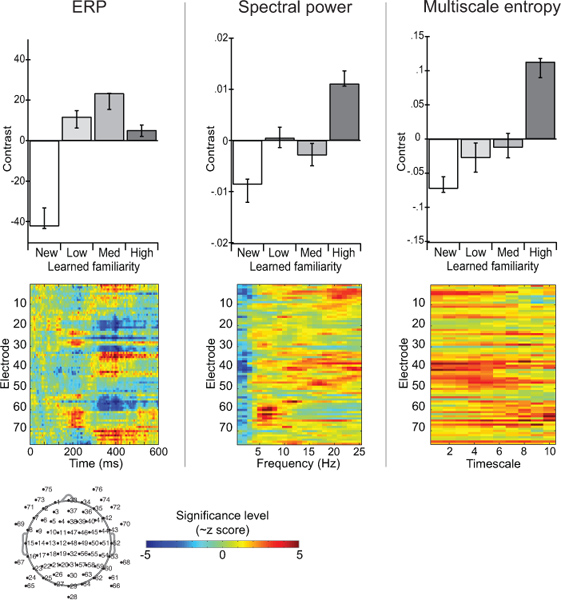
图7。对比脑电图跨ERP，功率谱，多尺度熵措施应对学到的面孔。条形图描述之间的对比确定的条件偏最小二乘分析^11。图像情节突出这种反差是最稳定的，由引导的时空分布。值代表〜z评分和，负值代表意义的逆条件影响。 点击这里查看大图 。

讨论

本文章的目的是提供一个概念和方法的描述，因为它适用于脑电图的神经影像数据的多尺度熵（MSE）。脑电图是一种强大的非侵入性神经影像学技术，具有高时间分辨率测量神经网络活动。 EEG信号反映人口锥体细胞突触后活动在皮层，其集体应对各种兴奋和抑制折返连接修改。因此，有多种方法来分析脑电图数据，每个方法的数据中提取独特的一面。

我们讨论了两种常见的分析方法：事件相关电位（ERP）分析和功率谱分析。 ERP分析捕获同步的EEG信号的相位锁定的离散事件发病的神经元活性。 ERP的反映具体的感性，电机，或认知操作，使得这个检查规范统计的理想IFIC处理阶段。功率谱分析量化的相对贡献特定频率的脑电信号。各种兴奋性和抑制性反馈回路相互作用夹带在某一特定频率^1,3的神经元群体的活性。不同脑区之间的这种同步被认为是推动跨越广泛的神经网络信息的结合。有丰富的文献支持特定频率范围内的功率和特定情绪或认知功能状态³之间的联系。

脑电图分析时，同样重要的是要记住，神经网络是复杂的系统与非线性动力学。这种复杂性是反映在EEG信号为不规则的振荡是不无意义的背景噪声的后果。像同步振荡活动，各种兴奋和抑制折返环路之间的相互作用引起短暂的流感ctuations大脑中的信号随着时间的推移^6。这样的瞬变被视为可反映网络微观状态之间的过渡或分岔，可以用来判断的程度的自由或底层网络的复杂性中的信号随时间的振幅模式的更大的可变性是表示更复杂的系统^5。重要的是，ERP或功率谱分析是不敏感，这种不规则的活动，而MSE。此外，网络的复杂性指数不能获得通过简单的计数活跃的大脑区域的数量，因为这样的方法是盲目的瞬态和动态递归大脑区域之间的相互作用。

互补性神经影像学分析方法结合起来，建立一个完整的画面相关的神经活动。更多的传统应用神经影像数据，如ERP和功率谱，结果的解释是增强措施的复杂性，如MSE，MSE提供了一种方法来捕捉一个特定的认知操作，有助于在多个时间尺度的大脑活动模式的时空序列变化。应用MSE新的和现有的数据集可能会提供进一步洞察认知如何从神经网络的动态。

材料

Name	Company	Catalog Number	Comments
EEG	BioSemi