EEGニューロイメージングデータの応用：事象関連電位、スペクトルパワー、およびマルチスケールエントロピー

要約

神経画像研究者は一般的に繰り返される実験的な試行を越え、平均活動として脳の応答を考慮すると "ノイズ"のように時間をかけて信号の変動を無視してください。しかし、そのノイズ信号があることが明らかになりつつある。この記事では、時間領域の脳信号のばらつきを定量化するためのマルチスケールエントロピーの新規な方法を説明します。

要約

人間の神経画像データを考慮すると、信号の変動の感謝は、我々は脳の信号についての考え方を根本的に革新を表しています。一般的に、研究者は、繰り返し実験試行にわたる平均として脳の応答を表し、 "ノイズ"と時間をかけて信号の変動を無視してください。しかしながら、脳信号ばらつきがニューラルネットワークのダイナミクスについての意味のある機能情報を伝達することが明らかになってきている。この記事では、脳の信号のばらつきを定量化するためのマルチスケールエントロピー（MSE）の新規な方法を説明します。それはスケール依存性とデータの線形および非線形ダイナミクスに対する感度を示していますので、MSEは、ニューラルネットワークダイナミクスの特に有益かもしれません。

概要

ニューロイメージングの最近の進歩は劇的に脳機能の理解を増強しています。しかし、神経画像データのアプリケーションの多くは、彼らがリアルタイムで展開として認知操作を重視しなく静的状態ではなく、脳のビューを強化する傾向がある。従って、少しは、脳網の時空間構造については、どのように複数の時間スケールを横切る時空間パターンの変化の順序が特定の認知動作に寄与することが知られている。現在の記事は、マルチスケールエントロピー^{（MSE）5、}複数の時間スケールにわたる脳機能ネットワーク通信でどのように異なる神経発電機に関する情報を提供することにより、特定の認知操作の基礎となる時空間パターンの複雑さを調べ、データを神経画像のための新しい分析ツールについて説明します。

情報理論、数学^7,16の適用された枝から派生し、MSEはオリジナルだった心電図⁴の複雑さを調べるために設計さLY。理論的には、MSEは、任意の時系列の複雑さを分析するために使用することができ、必要なプライマリは、信号の時系列が連続する時間の少なくとも50のデータポイントを含んでいることである。ただし、データにスケール依存性と線形および非線形ダイナミクスに対する感度は、ニューラルネットワークのダイナミクスのMSEは特に有益なことがあります。

ここでは、データ^9,12を神経画像脳波（EEG）にMSEの応用に焦点を当てています。脳波は、頭皮上に配置された電極は、新皮質¹のニューロンの集団のシナプス応答を捉えることにより、非侵襲的神経画像技術です。高い時間分解能で、脳波を簡単に一般的な取得プロトコルを変更することなく、MSEの必要な時系列の長さを満たしています。 EEGデータへのMSEのアプリケーションの有用性を強調するために、我々は、より伝統的なアプローチ税込でこの新規な方法を比較事象関連電位とスペクトルパワーをuding。一緒に使用する場合、これらの相補的な分析方法は、認知を生じさせるニューラルネットワーク運用さらなる洞察をもたらすことができるデータのより完全な説明を提供する。

プロトコル

1。 EEG取得

1. 参加者に実験手順を説明し、インフォームドコンセントを得る。
2. ドロップダウンの電極を適用します。ドロップダウン電極をアルコール綿棒を使用して配置されますの顔にクリーンエリア。
3. 参加者の頭の上に電極キャップを置きます。参加者の頭囲を測定し、適切なキャップのサイズを選択します。電極配置のための国際的に認められた10〜20システムに続いて、正中線に沿って[後からイニオンまでの距離を測定し、10％で割る。その番号を使用して、[後]とマークからまで測定。このマークの付いた電極キャップ位置Fpとの位置を合わせ、キャップを引き戻す。キャップの中心が鼻に沿ったものであることを確認してください。 Czのに[後]を測定し、この距離は[後からイニオンまでの距離の半分であることを確認します。ヒゲを締めます。
4. 電極ホルダーに置き、ゲルを充填した鈍ポイント注射。ゲルの導電性の列を作成するには、と接触して開始頭皮は、その後絞ると引き戻す。あまりにもゲルのアプリケーションは、隣接する電極の信号を埋める可能性があることに注意してください。
5. 電極ホルダーにアクティブ電極を固定します。
6. 実験に適した距離でモニターの前の被写体を配置します。きれいな記録のために目の動きや点滅を最小限に抑えることの重要性を強調し、まだ残っているため、参加者に依頼してください。
7. 買収コンピュータに電極接続とEEG信号品質を調べます。全ての電極オフセットが低い（<40 mVの）と安定していることを確認します。特定の電極に問題がある場合は、その電極を取り出して、そのサイトでのインピーダンスを調整するためにゲルを再適用します。
8. ファイルを保存し、実験を開始します。

2。脳波解析

1. 実験後に、しかし、関心のある特定の統計量を抽出する前に、前処理フィルタリングの標準的な手順を使用して成果物を除去するための継続的なEEGデータNDアーティファクト拒絶。このような写真の提示など、各離散事象に対応する時代に連続EEGをカット。各エポックでは、ベースラインとして100ミリ秒前刺激ウィンドウが含まれています。
2. 事象関連電位（ERP）の分析では、イベントの発症に位相ロックされている同期の脳活動をキャプチャします。背景活動（ すなわち非位相ロック） "うるさい"から誘発反応を分離する試験全体の平均。試験および被験者間にわたる変動は、分析のERP法の大きな課題を提示します。良好な信号対雑音比を達成するために、実験プロトコルが定義可能な発症と多くの離散的イベントを含むべきである。顕著なイベントの発症に対する脳の応答をロックした後、イベントのような多くを平均時間は、このノイズのいくつかを減らすのに役立ちますが、この手順で作成された一時的な同期は、典型的には、1秒以内に溶解する。各サブ用のERP成分ピークの振幅と潜時を特定JECT（ERP分析に関する詳細なガイドラインについて、ピクトンらを参照してください。、2000）。
3. フーリエ解析を使用して、時間領域から周波数領域にEEG信号を変換し、周波数^6を変化させる複合的な正弦波に信号を分解する。
4. マルチスケールエントロピー（MSE）が時間をかけて、複数の時間スケールにわたるneuroelectical信号のばらつきを推定情報理論的メトリックです。 MSE分析の概念的な描写を提供するために、2つのシミュレーション波形、定期的な波形ともっと確率いずれかを検討。サンプルエントロピーの値は、通常の波形に対してほぼゼロであり、より可変波形に対して2.5〜。試料エントロピーの増加は、情報理論によれば、基礎となるシステム^7,16の情報処理能力の量の増加として解釈することができ、信号の複雑さの増加に対応する。脳の容量が固定されていないことに注意してくださいますが、変更はDEPE神経コンテキスト^2、上nding 機能的には、特定の時点で接続することが起こる脳の領域、すなわち 。
5. MSEを計算するには、で入手可能なアルゴリズムが使用www.physionet.org/physiotools/mse/二段階でMSEを計算し、。
6. まず、アルゴリズム次第にダウンサンプルトライアル当たり、条件ごとに脳波の時系列。様々な時間スケールの複数の時系列を生成するダウンサンプリング元の時系列。時系列1は、元の時系列である。後続のタイムスケールの時系列を作成するために、スケールの長さと平均の非重複窓各ウィンドウ内のデータ·ポイントに元の時系列を分割する。ダウンサンプリングは、ローパスフィルタ処理と同様である。スケールによってサンプリング周波数を分周します近似信号はローパスその特定の時間スケールでフィルタされる頻度。パーにMSEの応用ticular周波数範囲（ 例えば 、アルファ：22.9 Hzから12 Hz）をその範囲内リズムの組成物、並びにそれらの周波数との間の相互作用を表すと解釈することができる。
7. 次に、アルゴリズムは、各粒度の粗い時系列¹⁴のサンプルのエントロピーを計算する。サンプルのエントロピーは、時系列の複雑さを推定する。 EEGの非線形解析では、一方では、個々の時系列は、基礎となる多次元非線形動的モデル（スタムを参照して、レビューのための2005）の症状を表していることを前提としています。この例では、mが（パターン長）毎に時系列の振幅パターンの変動が2対3つの連続した​​配列パターンを考慮することによって二次元対三次元空間で表現されることを意味2つに設定されているデータ点は、それぞれ。係数r（類似度判定基準）は、データを指し、その中の振幅範囲（色付きのバンドの高さによって示される）を反映再度、 "一致"と見なさ。パラメータの選択に関する詳細な手順については、湖を参照してください。100以上のデータポイントを持つ典型的な脳波の時系列では、0.5および1（リッチマンとムアマン、2000年を参照の間の値に等しい2に等しいパラメータmとパラメータrを設定ら、2002）。
   このシミュレートされた時系列のサンプルエントロピーを計算するには、最初の2つの成分​​のシーケンスパターン、赤橙色で始まります。まず、赤橙色の配列パターンが時系列的に発生する回数をカウントし、この2成分シーケンスの10件がある。第二、第三成分の配列パターンは、赤、橙黄色、時系列的に発生する回数をカウント、この三成分シーケンスの5マッチがある。次の二つの成分シーケンス（橙黄色）と時系列の次の三成分のシーケンス（オレンジ黄緑）のために同じ操作を続行します。これらsequenための2つの成分​​の一致（5）および三成分届い（3）数CESは、以前の値（;合計三成分届い= 8合計二成分届い= 15）を添加する。三成分の一致への2つの成分​​が一致したの合計比率を決定するために、 - 時系列内の他のすべてのシーケンスの一致（オス、最大Nまで）のために繰り返します。サンプルのエントロピーは、この比の自然対数である。各被験者は、各スケールのための単一のトライアルエントロピー対策にわたる平均としてチャネル固有MSE推定値を計算する。

結果

図1Aおよび2Aは、顔画像の提示に応答して、EEG信号を表す。裁判のように渡って平均化ERPコンポーネントと呼ばれる正と負のたわみのシリーズで構成されていたERP波形を生成します。 図1Bが示す単一の件名と、図6Aのための平均波形は、被験者のグループのための壮大な平均的な波形を示しています。特定の知覚、運動、または認知動作に各ERPコンポーネントに関する豊富な文献がある。例えば、N170は、約170ミリ秒後に刺激発症のピークとは、顔処理^8,15に関与しているという負のたわみである。

図2Bは、成分の周波数帯域にその同じEEG信号の分解を示す。スペクトル電力解析からの結果は、それによって信号の周波数成分（ 図2C）を明らかにする特定の周波数での電力の増加は、EEG信号内のそのリズムの存在の増加を反映している。

スペクトルパワーのように、MSEは、信号に寄与する振動の成分の複雑に敏感です。しかし、スペクトルパワーとは違って、MSEはまた、周波数成分（ すなわち非線形ダイナミクス^18）との間の相互作用に敏感である。 EEG信号の複雑さは、複数のタイムスケール上の試料エントロピー（ 図5）（図4）の関数として表される。 図3に示すように、試料のエントロピーは、信号のランダム性の程度との定期的な信号と上昇しても低い。そのランダム性の程度に増加、伝統的なエントロピーの措置とは異なり、マルチスケールエントロピーは、複数の時間スケールにわたるエントロピーを考慮することによってホワイトノイズからの複雑な信号を区別することができます。たとえば、コスタら 、2005と比較してマルチスケールエントロピー値Fまたは無相関（白色）ノイズ対相関（ピンク）ノイズ。サンプルエントロピーは細かいスケールでピンクノイズもホワイトノイズのために大きかったが、反対は粗いタイムスケール5-20で観察された。換言すれば、エントロピーが複数の時間スケールにわたって考えられていた場合には、信号の真の複雑度をより正確に単一のタイムスケールが考慮された場合であるよりも表現した。コントラストが細かい対粗いで異なるができるクロスオーバー効果のように）1）すべての時間スケールで同じ方法で、2）いくつかの時間スケールではなく、他の、または3ではない：特定のコントラストの時間的ダイナミクスによって、条件の効果が発現させることができるタイムスケール。

図6は、顔写真⁹の初期の対繰り返しプレゼンテーションを対照的なERPの条件の違い（ 図6A）、スペクトルパワー（ 図6B）、MSE（図6C）を示す。この例では、すべての措置は、明らかに収束同じ効果は、それは結果の解釈を制約としてしかし、顔の繰り返しに付属のサンプルエントロピーの減少が観察されたことが重要です。複雑さの減少は、基礎となるネットワークの機能をより単純かつより少ない情報を処理することができることを示唆している。

図7には、ERP、スペクトルパワーとMSEに適用された部分最小二乗¹¹の多変量解析からの統計結果を示す。実験は別の顔（Heisz ら 、2012）に関連付けられた親しみを操作した。コントラスト（棒グラフ）は、ERP振幅が見慣れた顔からではなく、事前の暴露量で変化見慣れた顔の間で新たな顔を区別を示しています。区別スペクトルパワーは、取得された親しみやすさに応じて直面したが正確に、中、低馴染みの顔を区別しませんでした。 MSEはそのサンプルエントロピー値さを増加させるの条件の違いに最も敏感だった増加顔親しみとED。イメージプロットは全ての電極および時間/周波数/タイムスケールを越え条件効果の時空間分布を捉える。この例では、MSEによるEEGの分析がERPまたはスペクトル電力の従来の方法を用いて得られなかった固有情報を生成した状況を示している。 MSEのこの相違は、条件はおそらく様々な周波数成分間の相互作用を含む、それらのネットワークダイナミクスの非線形態様に関して異なっていることを示唆している。

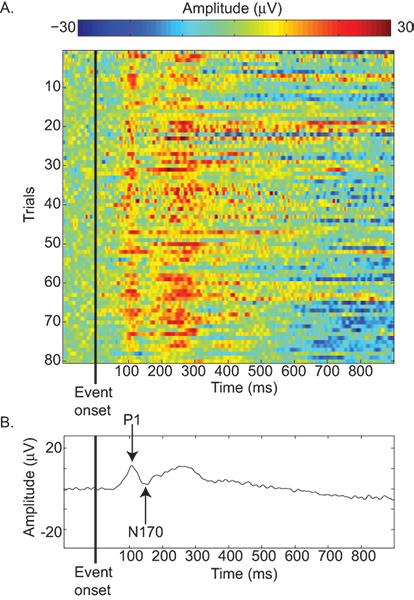
図1。）各試験のベースラインからの振幅たわみの関数として、一人の被験者の脳波応答は裁判の発症からの時間に対してプロットした。各試験は、顔画像の写真の提示から成っていた。正の振幅の偏向はに示されている赤、負の振幅偏向は青で示されている。すべての試験は、イベントに関連した位相ロック活動を示し、100ミリと250ミリ秒周りの正偏差を示しています。B）、図1Aに示すようにすべての試験全体で平均化は、イベント関連のコンポーネントと呼ばれ、名前の異なる正と負のたわみと平均ERP波形を生成標準の命名法による。例えば、P1は最初の正方向の成分であり、N170は、約170ミリ秒後に刺激発症のピーク、負のコンポーネントです。

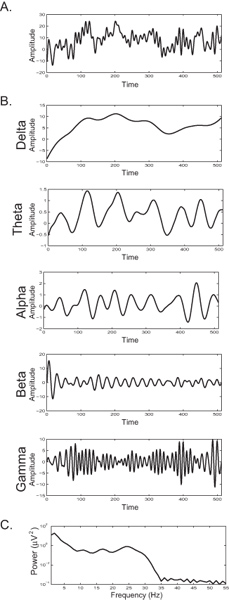
図2時間（データポイントで、速度512 Hzでのサンプリング）。B）デルタの周波数帯域を分離するフィルタ図2AバンドパスのEEG応答によって振幅をプロットシングル裁判のための単一の被写体の）EEG応答図に示されているEEG応答（0-4 Hz）で、シータ（5-8 Hz）で、アルファ（9-12 Hz）を、ベータ（13-30 Hz）で、ガンマ（> 30 Hz）です。C）スペクトル電力密度周波数による電力の関数としての信号の周波数構成を示す図2A。特定の周波数でのスペクトルパワーの増加は、その特定の周波数帯域内に同伴同期アクティブな神経細胞の数の増加を反映しているより大きい数字を表示するには、ここをクリックしてください 。

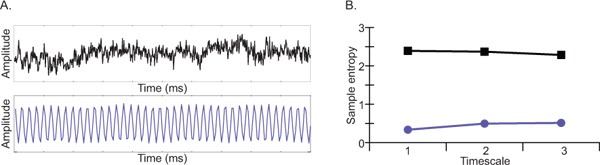
図3）二つのシミュレーション波形：。紫色で示されている定期的または予測可能な波形と、黒で描かれ、より確率波形B）最初の三つのタイムスケールのための2つのシミュレーション波形のサンプルエントロピー値。サンプルENTROPYはより確率信号よりも高い予測可能な信号に対して低くなっています。 大きい数字を表示するには、ここをクリックしてください 。

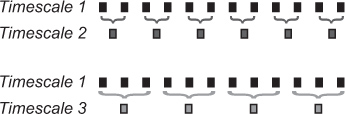
図4。ダウンサンプリング元の時系列変化する時間スケールの複数の時系列を生成する。1タイムスケールは、元の時系列である。スケール2の時系列は、各ウィンドウ内で長さが2であり、平均データ点の非オーバーラップウィンドウに元の時系列を分割することによって作成される。後続のタイムスケールの時系列を生成するために、スケールの長さと平均の非重複窓各ウィンドウ内のデータ·ポイントに元の時系列を分割する。

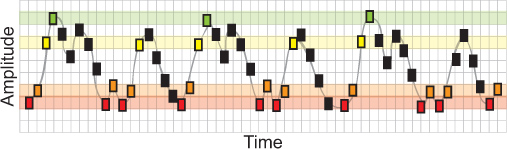
図5。各四角形は時系列サンプル·エントロピーの単一のデータポイントを表すシミュレーション波形は、時系列の変動を推定する。この例では、mが （パターン長）毎に時系列の振幅パターンの変動が2対3つの連続した配列パターンを考慮することによって二次元対三次元空間で表現されることを意味2つに設定されているデータ点は、それぞれ、rは （類似度判定基準）、データポイントが"一致"とみなされる範囲内の振幅範囲（色付きのバンドの高さによって示される）反射する。このシミュレートされた時系列のサンプルエントロピーを計算するには、最初の2つの成分​​のシーケンスパターン、赤橙色で始まります。まず、赤橙色の配列パターンが時系列的に発生する回数をカウントし、この2成分シーケンスの10件がある。第二、第三回成分系列パターンの数をカウントし、赤橙色 - エールOWは、時系列的に発生し、この三成分シーケンスの5試合があります。次の二つの成分の配列（橙黄色）と3つの成分のシーケンス（オレンジ黄緑）のために、このように続けます。これらの配列のための2つの成分​​の一致（5）および三成分届い（3）の数は、前の値（;合計三成分届い= 8合計二成分一致する= 15）を添加する。三成分の一致への2つの成分​​が一致したの合計比率を決定するために、 - 時系列内の他のすべてのシーケンスの一致（オス、最大Nまで）のために繰り返します。サンプルのエントロピーは、この比の自然対数である。各被験者は、各スケールのための単一のトライアルエントロピー対策にわたる平均としてチャネル固有MSE推定値を計算する。

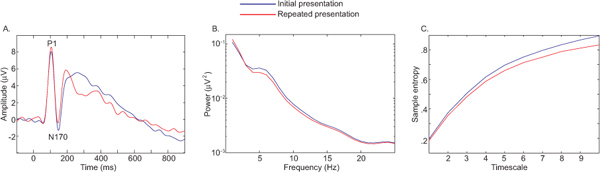
図6。ERPにおける条件の違い（）、スペクトルパワー（B）は 、顔の写真の初期の対繰り返しプレゼンテーションを対比MSEは（C） より大きい数字を表示するには、ここをクリックしてください 。

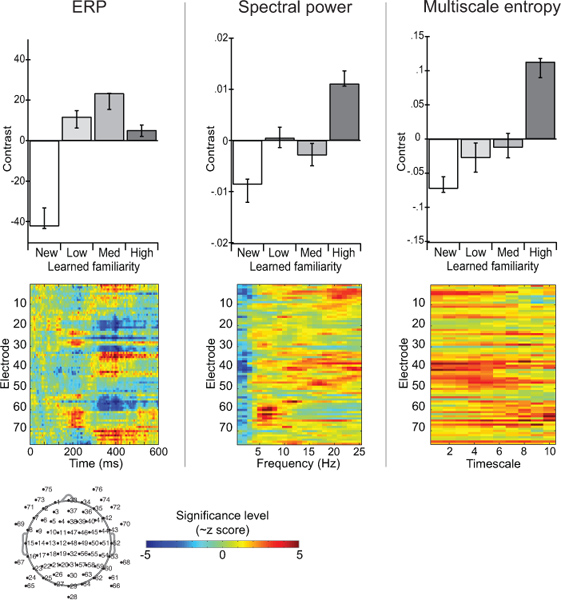
図7。 ERP、スペクトルパワー、およびマルチスケールエントロピーの施策を通して学習された面にEEG反応を対比。棒グラフには、少なくとも部分的二乗分析¹¹によって決定された条件の間のコントラストを描く。イメージプロットはブートストラップによって決定されるように、このコントラストは最も安定したときの時空間分布を強調しています。値は、A〜Zスコアを表し、負の値は逆の状態効果を意味を表している。 大きい数字を表示するには、ここをクリックしてください 。

ディスカッション

現在の記事の目標は、それが脳波神経画像データに適用されるマルチスケールエントロピー（MSE）の概念と方法論的な説明を提供することでした。 EEGは、高い時間分解能と神経回路網の活動を測定し、強力な非侵襲的神経画像技術です。 EEG信号は、集団応答さまざまな興奮性と抑制リエントラント接続によって変更される皮質の錐体細胞の集団の後シナプス活性を反映している。したがって、脳波データを分析し、各メソッドは、データのユニークな側面を抽出するために複数の方法があります。

事象関連電位（ERP）分析とスペクトル電力解析：我々は分析の2つの一般的な方法について議論した。 ERP分析は離散事象の発症に位相ロックされるEEG信号に同期神経活動をキャプチャします。事象関連電位は、スペックを調べるため、この統計の理想を作り、具体的な知覚、運動、または認知操作を反映するIFICの処理段階。スペクトルパワー分析はEEG信号に特定の周波数の相対的な寄与を定量化。様々な興奮性と抑制性のフィードバックループは同調に特定の周波数^1,3における神経集団の活動を相互に作用。異なる脳領域間のこのような同期は、広範な神経回路網を介して情報の結合を促進すると考えられている。特定の周波数範囲内の電力と機能^3、特定の感情や認知の状態との間のリンクをサポートする豊富な文献がある。

脳波分析するときには、ニューラルネットワークは非線形ダイナミクスを持つ複雑なシステムであることを心に留めておくことも重要です。このような複雑さは無意味、バックグラウンドノイズの結果ではない不規則な振動としてEEG信号に反映されます。同期振動活動と同様に、各種の興奮性と抑制リエントラントループ間の相互作用は一過性のインフルエンザを引き起こす時間⁶以上の脳信号でctuations。このような過渡現象は、基礎となるネットワークの自由度や複雑度を推定するために使用できるネットワーク微視的間の遷移又は分岐を反映すると考えられている。経時的な信号の振幅パターンにおける大きなばらつきがより複雑なシステム⁵を示している。 MSEがあるのに対し、批判的に、ERPやスペクトルパワー分析は、このような不規則な活動には区別されません。また、ネットワークの複雑さのインデックスは、このような方法は、脳領域間の過渡的および動的な再発性相互作用に盲目で単にアクティブ脳領域の数をカウントすることによって得ることができない。

分析を神経画像のための補完的な方法は、基礎となる神経活動の全体像を作成するために組み合わせる。 ERPやスペクトルパワーなど神経画像データ、より伝統的なアプリケーションからの結果の解釈は、MSのような複雑さの尺度により増強されE; MSEは、特定の認知操作に貢献し、複数の時間スケールにわたる脳活動の時空間パターンの変化のシーケンスをキャプチャする方法を提供します。新規および既存のデータセットにMSEを適用すると、認知は、ニューラルネットワークダイナミクスから射出方法さらなる洞察を提供することができる。

資料

Name	Company	Catalog Number	Comments
EEG	BioSemi