11.21 : Lattice Centering and Coordination Number

The structure of a crystalline solid, whether a metal or not, is best described by considering its simplest repeating unit, which is referred to as its unit cell. The unit cell consists of lattice points that represent the locations of atoms or ions. The entire structure then consists of this unit cell repeating in three dimensions. The three different types of unit cells present in the cubic lattice are illustrated in Figure 1.

Types of Unit Cells

Imagine taking a large number of identical spheres and arranging them uniformly in a container such that one layer is directly above the spheres in the layer below. This arrangement is called a simple cubic structure, and the unit cell is called the simple cubic unit cell or primitive cubic unit cell. In a simple cubic structure, the spheres are not packed as closely as they could be, and they only “fill” about 52% of the volume of the container.

An atom in this type of arrangement contacts only the four nearest neighbors in its layer; one atom directly above it in the layer above; and one atom directly below it in the layer below. The number of other particles that each particle in a crystalline solid contact is known as its coordination number. For a polonium atom in a simple cubic array, the coordination number is, therefore, six.

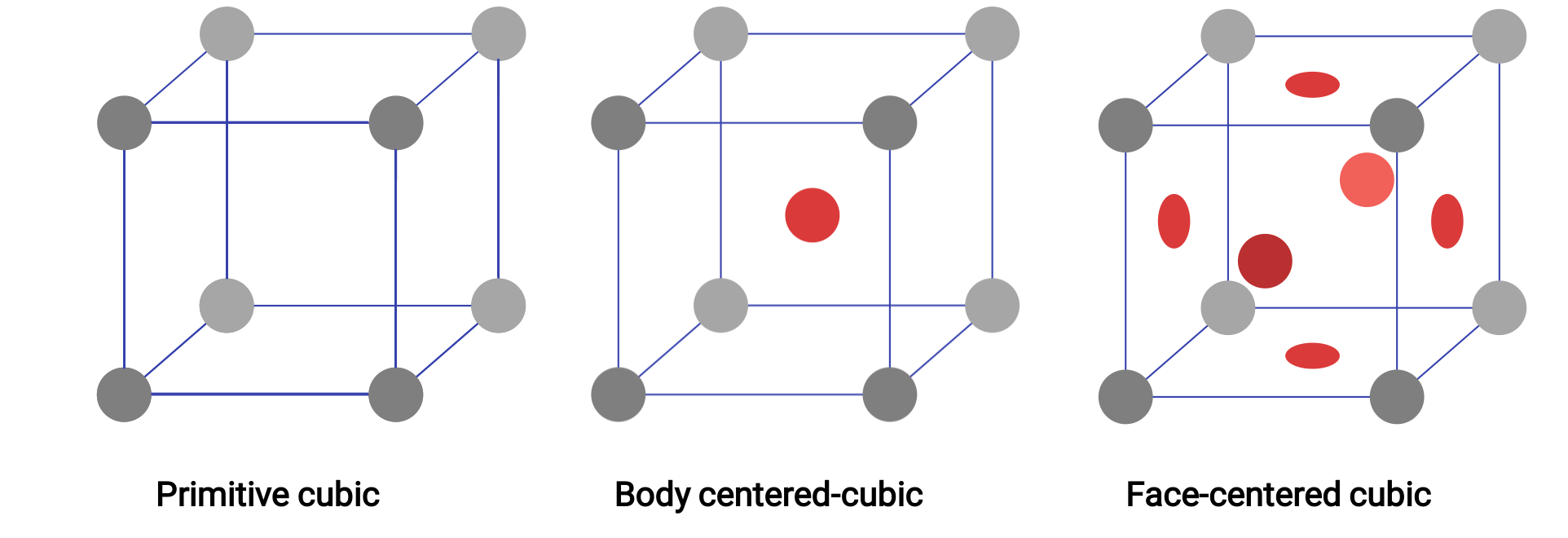
Figure 1. Three different crystal lattice structures exhibited by the cubic lattice systems.

In a primitive cubic lattice, the unit cell that repeats in all directions is a cube defined by the centers of eight atoms. Atoms at adjacent corners of this unit cell contact each other, so a cubic unit cell contains only the parts of these atoms that are within it. Since an atom at a corner of a simple cubic unit cell is contained by a total of eight unit cells, only one-eighth of that atom is within a specific unit cell. And since each simple cubic unit cell has one atom at each of its eight “corners,” there is 8 × 1/8= 1 atom within one simple cubic unit cell.

Some metals crystallize in an arrangement that has a cubic unit cell with atoms at all of the corners and an atom in the center. This is called a body-centered cubic (BCC) solid. Atoms in the corners of a BCC unit cell do not contact each other but contact the atom in the center. A BCC unit cell contains two atoms: one-eighth of an atom at each of the eight corners (8 × 1/8= 1 atom from the corners) plus one atom from the center. Any atom in this structure touches four atoms in the layer above it and four atoms in the layer below it. Thus, an atom in a BCC structure has a coordination number of eight. Atoms in BCC arrangements are much more efficiently packed than in a simple cubic structure, occupying about 68% of the total volume.

Many other metals crystallize in an arrangement that has a cubic unit cell with atoms at all of the corners and at the centers of each face. This arrangement is called a face-centered cubic (FCC) solid. A FCC unit cell contains four atoms: one-eighth of an atom at each of the eight corners (8 × 1/8= 1 atom from the corners) and one-half of an atom on each of the six faces (6 × 1/2= 3 atoms from the faces). The atoms at the corners touch the atoms in the centers of the adjacent faces along the face diagonals of the cube. Because the atoms are on identical lattice points, they have identical environments. Atoms in an FCC arrangement are packed as closely together as possible, with atoms occupying 74% of the volume. Each atom contacts six atoms in its own layer, three in the layer above, and three in the layer below. In this arrangement, each atom touches 12 near neighbors and therefore has a coordination number of 12.

This text has been adapted from Openstax, Chemistry 2e, Sections 10.5 The Solid State of Matter, and 10.6 Lattice Structures in Crystalline Solids.