8.9 : Force and Potential Energy in One Dimension

Force can be calculated from the expression for potential energy, which is a function of position. The component of a conservative force, in a particular direction, equals the negative of the derivative of the corresponding potential energy with respect to the displacement in that direction. For regions where potential energy changes rapidly with displacement, the work done and force is maximum. Also, when force is applied along the positive coordinate axis, the potential energy decreases with an increase in displacement. Hence, force and the derivative of potential energy with respect to displacement have opposite signs.

For instance, if the potential energy of a particle undergoing one-dimensional motion along the x-axis is

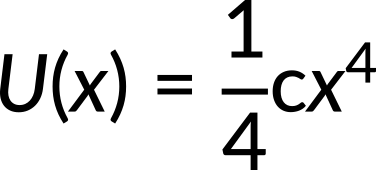
where c = 8 N/m³, what will the force be for the given potential energy? Here, the known quantity is potential energy. The unknown quantity force needs to be calculated.

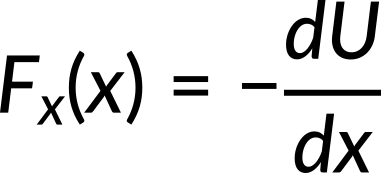
Incorporating the value of potential energy in the above expression, the force along the x-direction is calculated to be −cx³. Substituting the value of c, the force is calculated to be −8x³.

The potential energy function for the force between two atoms in a diatomic molecule is approximately given by

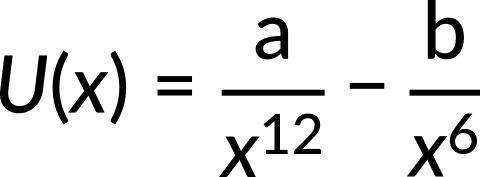
where a and b are constants and x is the distance between the atoms. If the dissociation energy of the molecule is

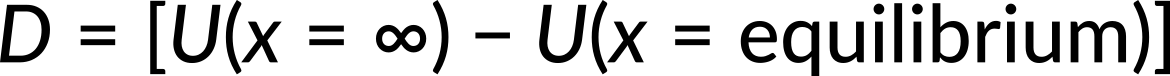
what is the value of D? Here, the known quantity is the potential energy. The unknown quantity is the dissociation energy of the molecule. Substituting the potential energy function, we get the expression for force. Since the net force is zero at equilibrium, we get

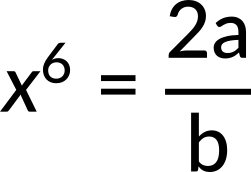
Now, the value of x⁶ is substituted in the expression for potential energy. Since potential energy at infinity is zero, the dissociation energy of the molecule is calculated to be b²/4a.

This text is adapted from Openstax, University Physics Volume 1, Section 8.4: Potential Energy Diagrams and Stability.