9.6 : Conservation of Momentum: Problem Solving
Solving problems using the conservation of momentum requires four basic steps:
- Identify a closed system, where the total mass is constant, and no net external force acts on it.
- Write down an expression representing the total momentum of the system before the interaction.
- Write down an expression representing the total momentum of the system after the interaction.
- Equate these two expressions to obtain the unknown quantity.
Let us apply these steps to solve a problem. Suppose two carts in a physics lab roll on a level surface with negligible friction. These carts have small magnets at their ends so that when they collide, they stick together. The first cart has a mass of 675 g and is rolling at 0.750 m/s to the right; the second has a mass of 500 g and is rolling at 1.33 m/s, also to the right. After the collision, what is the velocity of the two joined carts?
The system of two carts meets the requirements for a closed system: the combined mass of the two carts does not change, and while the carts exert forces on each other, those forces are internal to the system, so they do not change the momentum of the system as a whole. In the vertical direction, the weights of the carts are canceled by the normal forces on the carts from the track.
Here, the known quantities are the mass of cart 1 (m1 = 675 g), mass of cart 2 (m2 = 500 g), initial velocity of cart 1 (v1 = 0.750 m/s) and initial velocity of cart 2 (v2 = 1.33 m/s). The unknown quantity, the final velocity vf of the joined carts, needs to be calculated. As per the conservation of momentum, the initial momentum is equal to the final momentum. The direction of their initial velocity vectors is defined to be in the +x-direction. The initial momentum is then given by:
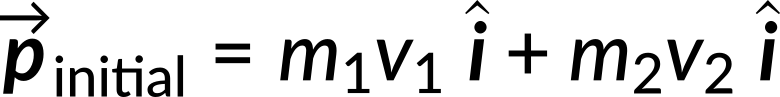
The final momentum of the joined carts is
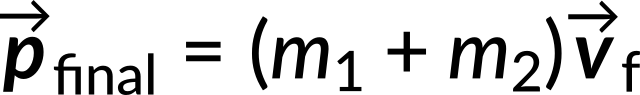
Equating both these equations, the final velocity is given by
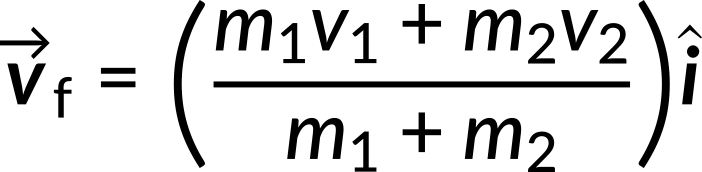
Substituting the known quantities in the above expression, the final velocity is 0.997 m/s in the x-direction.
This text is adapted from Openstax, University Physics Volume 1, Section 9.3: Conservation of Linear Momentum.
Aus Kapitel 9:

Now Playing
9.6 : Conservation of Momentum: Problem Solving
Linear Momentum, Impulse and Collisions
9.8K Ansichten

9.1 : Linearer Impuls
Linear Momentum, Impulse and Collisions
13.8K Ansichten

9.2 : Kraft und Schwung
Linear Momentum, Impulse and Collisions
15.3K Ansichten

9.3 : Impuls
Linear Momentum, Impulse and Collisions
18.4K Ansichten

9.4 : Impuls-Impuls-Satz
Linear Momentum, Impulse and Collisions
11.1K Ansichten

9.5 : Impulserhaltung: Einleitung
Linear Momentum, Impulse and Collisions
14.5K Ansichten

9.7 : Arten von Kollisionen - I
Linear Momentum, Impulse and Collisions
6.7K Ansichten

9.8 : Arten von Kollisionen - II
Linear Momentum, Impulse and Collisions
7.2K Ansichten

9.9 : Elastische Kollisionen: Einführung
Linear Momentum, Impulse and Collisions
12.2K Ansichten

9.10 : Elastische Kollisionen: Fallstudie
Linear Momentum, Impulse and Collisions
13.4K Ansichten

9.11 : Kollisionen in mehreren Dimensionen: Einführung
Linear Momentum, Impulse and Collisions
4.8K Ansichten

9.12 : Kollisionen in mehreren Dimensionen: Problemlösung
Linear Momentum, Impulse and Collisions
3.6K Ansichten

9.13 : Schwerpunkt: Einführung
Linear Momentum, Impulse and Collisions
14.0K Ansichten

9.14 : Bedeutung des Massenschwerpunkts
Linear Momentum, Impulse and Collisions
6.2K Ansichten

9.15 : Potentielle Gravitationsenergie für ausgedehnte Objekte
Linear Momentum, Impulse and Collisions
1.3K Ansichten
See More
Copyright © 2025 MyJoVE Corporation. Alle Rechte vorbehalten