15.12 : Damped Oscillations
In the real world, oscillations seldom follow true simple harmonic motion. A system that continues its motion indefinitely without losing its amplitude is termed undamped. However, friction of some sort usually dampens the motion, so it fades away or needs more force to continue. For example, a guitar string stops oscillating a few seconds after being plucked. Similarly, one must continually push a swing to keep a child swinging on a playground.
Although friction and other non-conservative forces can be made negligibly small, complete undamped motion is rare. In fact, these non-conservative forces are often required to dampen oscillations, such as in-car shock absorbers. For a system that has a small amount of damping, the period and frequency are nearly the same as for simple harmonic motion, but the amplitude gradually decreases. This occurs because the non-conservative damping force removes energy from the system, usually in the form of thermal energy. In general, energy removal by non-conservative forces is described as
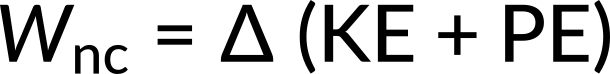
where Wnc is work done by a non-conservative force (here, the damping force). For a damped harmonic oscillator, Wnc is negative because it removes mechanical energy (KE + PE) from the system.
This text is adapted from Openstax, College Physics, Section 16.7: Damped Harmonic Motion and Openstax, University Physics Volume 1, Section 15.4: Damped Oscillations.
Aus Kapitel 15:

Now Playing
15.12 : Damped Oscillations
Oscillations
5.6K Ansichten

15.1 : Einfache harmonische Bewegung
Oscillations
9.3K Ansichten

15.2 : Eigenschaften der einfachen harmonischen Bewegung
Oscillations
12.6K Ansichten

15.3 : Oszillationen um eine Gleichgewichtsposition
Oscillations
5.3K Ansichten

15.4 : Energie in einfacher harmonischer Bewegung
Oscillations
8.8K Ansichten

15.5 : Häufigkeit des Feder-Masse-Systems
Oscillations
5.3K Ansichten

15.6 : Einfache harmonische Bewegung und gleichmäßige Kreisbewegung
Oscillations
4.2K Ansichten

15.7 : Problemlösung: Energie in einfacher harmonischer Bewegung
Oscillations
1.2K Ansichten

15.8 : Einfaches Pendel
Oscillations
4.6K Ansichten

15.9 : Torsionspendel
Oscillations
5.3K Ansichten

15.10 : Physikalisches Pendel
Oscillations
1.6K Ansichten

15.11 : Messung der Beschleunigung durch die Schwerkraft
Oscillations
526 Ansichten

15.13 : Arten der Dämpfung
Oscillations
6.4K Ansichten

15.14 : Erzwungene Schwingungen
Oscillations
6.5K Ansichten

15.15 : Konzept der Resonanz und ihre Eigenschaften
Oscillations
5.0K Ansichten
Copyright © 2025 MyJoVE Corporation. Alle Rechte vorbehalten