Neuer Rahmen für das Verständnis der hirnübergreifenden Kohärenz in funktionellen Hyperscanning-Studien der Nahinfrarotspektroskopie (fNIRS)

Zusammenfassung

Die Wavelet-Transformationskohärenz (WTC) ist eine gängige Methode zur Bewertung der Kopplung zwischen Signalen, die in Hyperscanning-Studien der funktionellen Nahinfrarotspektroskopie (fNIRS) verwendet wird. In dieser Arbeit wird ein Werkzeugkasten zur Beurteilung der Richtungsabhängigkeit der Signalwechselwirkung vorgestellt.

Zusammenfassung

Trotz der wachsenden Zahl von funktionellen Hyperscanning-Studien mit Nahinfrarotspektroskopie (fNIRS) scheint die Bewertung der Kopplung zwischen zwei neuronalen Signalen mittels Wavelet-Transformationskohärenz (WTC) die Richtungsabhängigkeit der Wechselwirkung zu ignorieren. Dem Feld fehlt derzeit ein Rahmen, der es den Forschern ermöglicht, zu bestimmen, ob ein hoher Kohärenzwert, der mit einer WTC-Funktion erhalten wurde, eine phasengleiche Synchronisation (d. h. eine neuronale Aktivierung wird in beiden Mitgliedern der Dyade gleichzeitig beobachtet), eine verzögerte Synchronisation (d. h. eine neuronale Aktivierung wird in einem Mitglied der Dyade vor dem anderen Mitglied beobachtet) widerspiegelt. oder Anti-Phasen-Synchronisation (d.h. die neuronale Aktivierung ist in einem Mitglied der Dyade erhöht und in dem anderen vermindert). Um diesem Bedarf gerecht zu werden, wird in dieser Arbeit ein komplementärer und sensitiverer Ansatz zur Analyse der Phasenkohärenz zweier neuronaler Signale vorgeschlagen. Die Toolbox ermöglicht es den Forschern, die Richtungsabhängigkeit der Kopplung abzuschätzen, indem sie die Phasenwinkelwerte, die mit herkömmlicher WTC ermittelt wurden, in phasengleiche Synchronisation, verzögerte Synchronisation und Antiphasensynchronisation klassifizieren. Die Toolbox ermöglicht es den Forschern auch, zu beurteilen, wie sich die Dynamik der Interaktionen während der Aufgabe entwickelt und verändert. Die Verwendung dieses neuartigen WTC-Ansatzes und der Toolbox wird unser Verständnis komplexer sozialer Interaktionen durch ihre Verwendung in fNIRS-Hyperscanning-Studien verbessern.

Einleitung

In den letzten Jahren hat sich die Art der Studien, die durchgeführt werden, um die neuronalen Grundlagen des Sozialverhaltens zu verstehen, verschoben ^1,2. Traditionell haben sich Studien in den sozialen Neurowissenschaften auf die neuronale Aktivierung in einem isolierten Gehirn während einer sozial relevanten Aufgabe konzentriert. Fortschritte in der Neuroimaging-Technologie ermöglichen es nun jedoch, die neuronale Aktivierung im Gehirn eines oder mehrerer Personen während sozialer Interaktion zu untersuchen, wie sie im "realen" Leben stattfindet³. Im "realen" Leben können sich Individuen frei bewegen, und die Muster der Gehirnaktivierung ändern sich wahrscheinlich, wenn Informationen ausgetauscht werden und die Sozialpartner Feedback voneinander erhalten⁴.

Hyperscanning ist eine Methode, die diesen bidirektionalen Informationsaustausch bewertet, indem die Gehirnaktivität von zwei oder mehr Personen gleichzeitig gemessen^{wird 5}. Eine neue Forschungsgruppe hat die funktionelle Nahinfrarotspektroskopie (fNIRS) eingesetzt, eine nicht-invasive Neuroimaging-Technik, die im Vergleich zu anderen bildgebenden Verfahren weniger anfällig für Bewegungsartefakte ist⁶. Hyperscanning über fNIRS ermöglicht die Beurteilung der Interhirnsynchronisation (IBS) in realen Umgebungen, während sich die interaktiven Partner frei und natürlich bewegen. Dies ist besonders relevant für die Arbeit mit Säuglingen und Kleinkindern, die in der Regel sehr aktiv sind. Es wurde berichtet, dass das Reizdarmsyndrom das gegenseitige Verständnis zwischen interaktiven Partnern widerspiegelt, das als Grundlage für effektive soziale Interaktion und Kommunikation dient und gemeinsame Intentionalität vermittelt ^1,7,8.

Es werden mehrere Methoden verwendet, um das Reizdarmsyndrom zweier Gehirne zu bewerten. Zu diesen Methoden gehören Zeitreihenkorrelationen, wie z.B. die Kreuzkorrelation und der Pearson-Korrelationskoeffizient ^9,10 (siehe eine Übersichtsarbeit von Scholkmann et ^al.10). Andere Methoden beinhalten die Bewertung der Stärke der Kopplung im Frequenzbereich. Zu diesen Methoden gehören der Phasensperrwert (PLV) und die Phasenkohärenz (siehe eine Übersichtsarbeit von Czeszumski et ^al.11). Eine der gebräuchlichsten Methoden in fNIRS-Studien verwendet die Wavelet-Transformationskohärenz (WTC) - ein Maß für die Kreuzkorrelation zweier Zeitreihen in Abhängigkeit von Frequenz und Zeit¹⁰.

WTC verwendet Korrelationsanalysen, um die Kohärenz und Phasenverschiebung zwischen zwei Zeitreihen im Zeit-Frequenz-Bereich zu berechnen. FNIRS-Hyperscanning-Studien haben WTC verwendet, um das Reizdarmsyndrom in vielen Funktionsbereichen zu schätzen, einschließlich Aktionsüberwachung 12, kooperatives und kompetitives Verhalten 5,13,14,15, Nachahmung 16, Mutter-Kind-Problemlösung 17 und Lehr-Lern-Verhalten ^18,19,20,21. Typischerweise wird in Hyperscanning-Studien die gehirnübergreifende Kohärenz, wie sie von WTC gemessen wird, während einer experimentellen Aufgabe mit der hirnübergreifenden Kohärenz während einer Kontrollaufgabe verglichen. Diese Ergebnisse werden in der Regel mit einem WTC-"Hot Plot" dargestellt, der die Kohärenz zwischen den beiden Gehirnen zu jedem Zeitpunkt und jeder Häufigkeit zeigt (siehe Abbildung 1).

Wie von Czesumaski et ^al.11 vorgeschlagen, hat sich WTC zum analytischen Standardansatz für die Analyse von fNIRS-Hyperscanning entwickelt. Die WTC-Analyse ist eine flexible, "werkzeugunabhängige" Methode zur Datenvisualisierung und -interpretation²². Die Kohärenzkoeffizienten-Heatmap, die eine narrative Form der Analyse bietet, die es ermöglicht, Perioden synchronen oder asynchronen Verhaltens sowie die Intensität der Gehirnaktivität während der Erledigung einer Aufgabe leicht zu identifizieren, ist der Hauptvorteil von WTC und macht es zu einem starken Werkzeug für die angewandte Forschung²². WTC hat einen Vorteil gegenüber Korrelationstechniken. Korrelationen sind empfindlich gegenüber der Form der hämodynamischen Reaktionsfunktion (HRF), von der angenommen wird, dass sie sich zwischen Individuen (insbesondere in Bezug auf das Alter) und zwischen verschiedenen Gehirnbereichen unterscheidet. Im Gegensatz dazu ist das WTC von interregionalen Veränderungen im (HRF)²³ nicht betroffen. Forscher haben den Wavelet-Ansatz verwendet, um fMRT-Zeitreihen zu untersuchen. Zhang et ^al.24 verglichen die häufig verwendeten funktionalen Konnektivitätsmetriken, einschließlich der Pearson-Korrelation, der partiellen Korrelation, der gegenseitigen Information und der Wavelet-Kohärenztransformation (WTC). Sie führten Klassifikationsexperimente mit groß angelegten funktionellen Konnektivitätsmustern durch, die aus fMRT-Daten aus dem Ruhezustand und fMRT-Daten mit natürlichem Stimulus beim Betrachten von Videos abgeleitet wurden. Ihre Ergebnisse deuteten darauf hin, dass WTC bei der Klassifizierung (Spezifität, Sensitivität und Genauigkeit) am besten abschneidet, was darauf hindeutet, dass WTC eine bevorzugte funktionelle Konnektivitätsmetrik für die Untersuchung funktioneller Gehirnnetzwerke ist, zumindest in Klassifikationsanwendungen²⁴.

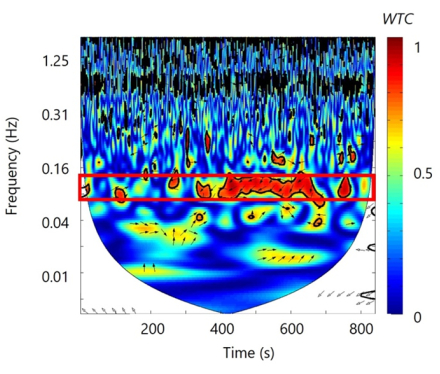
Abbildung 1: Kohärenz der Wavelet-Transformation (WTC). WTC zeigt die Kohärenz und den Phasenwinkel zwischen zwei Zeitreihen als Funktion sowohl der Zeit (x-Achse) als auch der Frequenz (y-Achse). Die Kohärenzerhöhung wird durch die rote Farbe im Diagramm dargestellt, und die kleinen Pfeile im Diagramm zeigen den Phasenwinkel der beiden Zeitreihen an. Der nach rechts zeigende Pfeil stellt die phasengleiche Synchronisierung dar. Die nach unten und nach oben zeigenden Pfeile stellen eine verzögerte Synchronisierung dar. und der nach links zeigende Pfeil stellt die Anti-Phasen-Synchronisation³⁰ dar. Diese Abbildung wurde von Pan et ^al.19 übernommen. Bitte klicken Sie hier, um eine größere Version dieser Abbildung anzuzeigen.

Kürzlich hat Hamilton²⁵ mehrere Einschränkungen bei der Interpretation von Cross-hirn-Kohärenzdaten in fNIRS-Hyperscanning-Studien artikuliert. Eines von Hamiltons Hauptanliegen war, dass Kohärenzmessungen (z.B. WTC) Effekte nur als symmetrisch melden (d.h. zwei Gehirne sind korreliert und zeigen das gleiche Veränderungsmuster). Viele soziale Interaktionen sind jedoch asymmetrisch (z. B. der Informationsfluss zwischen einem Sprecher und einem Zuhörer), da zwei Teilnehmer unterschiedliche Rollen spielen können, und es ist nicht klar, ob das WTC diese Informationen erfassen kann. Hier wird dieses Problem durch ein neues Framework gelöst, das eine einfache Interpretation der Cross-Wavelet-Leistung ermöglicht, indem die Cross-Wavelet-Phase zur Erkennung der Richtungsabhängigkeit verwendet wird. Dieser Rahmen ermöglicht es auch, zu untersuchen, wie sich die Dynamik von Interaktionen während einer Aufgabe entwickelt und verändert.

Während WTC- und Korrelationsmethoden die funktionelle Konnektivität bewerten, bewerten andere Methoden die effektive Konnektivität und versuchen, die kausalen Einflüsse eines neuronalen Elements auf ein anderes zu extrahieren. Die Transferentropie ist ein Maß aus der Informationstheorie, das den Transfer zwischen gemeinsam abhängigen Prozessen beschreibt²⁶. Eine weitere verwandte Methode ist die Granger-Kausalitätsanalyse (GCA), die als äquivalent zur Transferentropie²⁶ beschrieben wurde.

In der bestehenden Literatur zu fNIRS-Hyperscanning-Studien wurde die Granger-Kausalitätsanalyse (GCA) häufig verwendet, um die Kopplungsdirektionalität zwischen fNIRS-Zeitreihendaten abzuschätzen, die während einer Vielzahl verschiedener Aufgaben gewonnen wurden, wie z. B. Kooperation⁵, Unterricht¹⁹ und Nachahmung¹⁶. GCA verwendet vektorautoregressive Modelle, um die Richtungsabhängigkeit der Kopplung zwischen Zeitreihen in Gehirndaten zu bewerten. Die Kausalität von Granger basiert auf Vorhersage und Präzedenz: "Eine Variable X wird als 'G-Ursache' der Variablen Y bezeichnet, wenn die Vergangenheit von X die Informationen enthält, die helfen, die Zukunft von Y vorherzusagen, und zwar über Informationen, die bereits in der Vergangenheit von Y liegen"²⁷. Dementsprechend wird die G-Kausalität in zwei Richtungen analysiert: 1) von Subjekt A zu Subjekt B und 2) von Subjekt B zu Subjekt A.

Während die GCA-Analyse als ergänzende Analyse dient, die darauf abzielt, festzustellen, ob ein hoher Kohärenzwert, der mit einer WTC-Funktion erhalten wurde, eine IBS- oder verzögerte Synchronisation widerspiegelt (ein Signal führt zum anderen), ermöglicht sie nicht die Bestimmung, ob eine Antiphasensynchronisation stattgefunden hat. In traditionellen Neuroimaging-Studien, bei denen nur ein Teilnehmer gescannt wird (d. h. der "Single-Brain"-Ansatz), bedeutet ein Anti-Phasen-Muster, dass die Aktivität in einer Gehirnregion erhöht wird, während die Aktivität in der anderen Gehirnregion verringert wird²⁸. In der Hyperscanning-Literatur kann das Vorhandensein einer Anti-Phasen-Synchronisation darauf hindeuten, dass die neuronale Aktivierung bei einem Subjekt erhöht ist und gleichzeitig die neuronale Aktivierung bei dem anderen Subjekt verringert ist. Daher besteht die Notwendigkeit, ein umfassendes Modell bereitzustellen, das die Richtungsabhängigkeit erkennen kann. Genauer gesagt wird dieses Modell in der Lage sein, eine Anti-Phasen-Synchronisation (bei der die Aktivitätsrichtung eines Individuums der seines Partners entgegengesetzt ist) zusätzlich zu einer phasenweisen Synchronisation und einer verzögerten Synchronisation zu erkennen.

In einem Versuch, die Besorgnis auszuräumen, dass WTC nur symmetrische Effekte zeigt, bei denen beide Gehirne das gleiche Veränderungsmuster zeigen²⁵, wird ein neuer Ansatz zur Identifizierung der Art der Interaktion durch Untersuchung der Synchronisationsphase (d. h. phasengleich, verzögert oder anti-phasig) vorgestellt (siehe Abbildung 2). Zu diesem Zweck wurde eine Toolbox entwickelt, die die verschiedenen Arten von Wechselwirkungen mit der WTC-Methode klassifiziert. Die Arten von Wechselwirkungen werden anhand von relativen Phasendaten aus der Cross-Wavelet-Transformationsanalyse klassifiziert.

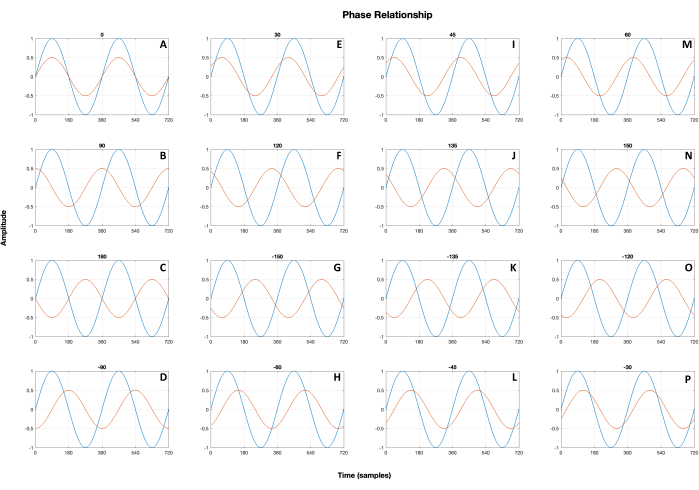
Abbildung 2: Darstellung der unterschiedlichen Phasenbeziehungen einfacher Sinuswelle. (A) Wenn die beiden Signale, Signal 1 (blaue Linie s) und Signal 2 (orangefarbene Linies), ihre jeweiligen Maximal-, Minimal- und Nullwerte zum gleichen Zeitpunkt erreichen, werden sie als phasensynchron³² bezeichnet. (B) Wenn ein Signal seinen Maximalwert erreicht und das andere Signal zum gleichen Zeitpunkt den Nullwert erreicht, wird von einer verzögerten Synchronisation gesprochen (eines führt um 90°)^32,33,34. (C) Wenn sich zwei Zeitreihen in entgegengesetzte Richtungen verschieben, d. h. ein Signal erreicht den Maximalwert und das andere den Minimalwert zum gleichen Zeitpunkt, wird dies als Anti-Phasen-Synchronisation²⁸ bezeichnet. (D-P) In allen anderen Phasenbeziehungen zwischen zwei Zeitreihen führt ein Signal das andere. In allen positiven Phasen ist Signal 2 führend gegenüber Signal 1 (z. B. Felder E, F, M und N), während Signal 1 in allen negativen Phasen vor Signal 2 steht (z. B. Felder D, G, H, O und P). Wenn der absolute Wert der Phase höher ist, wird es deutlicher, welche Zeitreihe die andere anführt (z. B. ist die Führung in Panel J ausgeprägter als in Panel I, und in Panel K ist die Führung ausgeprägter als in Panel L). Bitte klicken Sie hier, um eine größere Version dieser Abbildung anzuzeigen.

Protokoll

Die Studie wurde an der Florida Atlantic University (FAU) durchgeführt und vom FAU Institutional Review Board (IRB) genehmigt.

1. Verwendung der Homer3-Software (Table of Materials) zur Vorverarbeitung der fNIRS-Hyperscanning-Daten

HINWEIS: Homer3 ist eine MATLAB-Anwendung, die fNIRS-Daten analysiert, um Schätzungen und Karten der Gehirnaktivierung zu erhalten²⁹. Homer3 kann unter folgendem Link (https://openfnirs.org/software/homer/) heruntergeladen und installiert werden.

1. Öffnen Sie MATLAB und navigieren Sie zu dem Ordner, in dem die unformatierten NIRS-Dateien gespeichert sind. Wählen Sie den Ordner aus und öffnen Sie ihn.
2. Geben Sie Homer3 in das Befehlsfenster von MATLAB ein, um die Homer3-GUI zu starten. Homer3. erkennt die .nirs-Dateien und fordert zur Konvertierung in das .snirf-Format (ein universelles Dateiformat zum Speichern und Freigeben von NIRS-Daten unabhängig von einem bestimmten anwendungsspezifischen Dateiformat wie MATLAB) auf, um mit der Vorverarbeitung der Daten fortzufahren.
3. Nachdem Sie die .nirs-Dateien in das .snirf-Format in Homer3 importiert haben, klicken Sie in der Homer3-GUI auf die Option Extras und wählen Sie Processing Stream bearbeiten.
4. Wählen Sie in der ProcStreamEdit-GUI die Vorverarbeitungsschritte aus der Spalte Registry-Funktion in die Spalte Aktueller Verarbeitungs-Stream aus, indem Sie auf Hinzufügen klicken. Die enthaltenen Vorverarbeitungsschritte lauten wie folgt:
   1. Verwenden Sie hmrR_intensity2OD , um die Intensitätsdaten in optische Dichte umzuwandeln.
   2. Verwenden Sie hmrR_MotionCorrectWavelet , um Bewegungsartefakte mit der entsprechenden Filterfunktion zu korrigieren.
   3. Verwenden Sie hmrR_OD2conc , um die OD-Daten in die Konzentration umzuwandeln.
   4. Verwenden Sie hmR_BlockAvg, um den Blockdurchschnitt für Konzentrationsdaten zu berechnen.
      HINWEIS: Die Auswahl der Vorverarbeitungsschritte kann je nach Art des Datensatzes variieren.
5. Um den aktuellen Verarbeitungsdatenstrom zu speichern, klicken Sie auf die Option Speichern und beenden Sie dann die ProcStreamEdit-GUI.
6. Um den Vorverarbeitungs-Stream in der Haupt-GUI von Homer3 auszuführen, klicken Sie auf die Option AUSFÜHREN . Nachdem Homer3 die Ausführung des ausgewählten Verarbeitungsdatenstroms abgeschlossen hat, speichert es die vorverarbeiteten Zeitreihen für jeden Teilnehmer in einem .mat-Dateiformat, das Hbo, Hbr und Hbt für alle Kanäle und Ereignisse enthält. Ein Ordner mit dem Namen homer output wird von Homer3 im aktuell ausgewählten Ordner erstellt, um diese Dateien zu speichern.
7. Ein Ordner mit dem Namen derivatives wird von Homer3 im ausgewählten Ordner erstellt, um diese Dateien zu speichern. Wählen Sie den Homer-Ordner aus, der sich im Ordner "Derivate" befindet. Wählen Sie die .mat-Datei für jedes Gehirn aus und exportieren Sie Hbo, Hbr, Hbt.
   HINWEIS: Der Name des von Homer3 erstellten Ausgabeordners hängt von der Homer3-Version ab.

2. Erste Schritte mit der LeaderFollowerByPhase-Toolbox

1. Um die Art der Interaktion zu analysieren, die in einer Hyperscan-Aufzeichnung auftritt, verwenden Sie die Toolbox LeaderFollowerByPhase, wie in dem in Abbildung 3 gezeigten Prozess beschrieben. Wählen Sie in MATLAB die .mat-Dateien für jedes Gehirn aus und laden Sie die Hbo- (oder Hbr-) Daten des spezifischen Kanals und des spezifischen Ereignisses in einen eindimensionalen Vektor als signal1 und signal2.
2. Definieren Sie in der MATLAB-Befehlszeile die Parameter
   1. lowFreq, highFreq: Geben Sie lowFreq = [niedriger FOI] und highFreq = [hoher FOI] ein. Die Standardwerte sind lowFreq = 0,01 Hz, highFreq = 1 Hz.
      HINWEIS: Die Parameter der Funktionen lowFreq und highFreq definieren den FOI-Bereich (Frequency of Interest). WTC berechnet die Kohärenz zwischen den beiden Gehirnen zu jedem Zeitpunkt und jeder Frequenz. Die Kohärenzwerte werden in der Regel innerhalb eines bestimmten FOI gemittelt.
   2. Definieren Sie den Parameter phaseRange; type phaseRange = [Bereich in Grad].
      HINWEIS: Der Standardwert ist phaseRange = 90°. Die Phase liegt zwischen 0° und 360° aufgrund der zirkulären Modulo-Natur der Phase. Die Phasenbereiche werden nach einem Bereich unterteilt, der vier Punkte umgibt. In der vorgestellten Toolbox wird ein neuer Ansatz zur Klassifizierung asymmetrischer Wechselwirkungen vorgestellt (Abbildung 4), indem die Richtungsabhängigkeit der Kopplung unter Verwendung der Phasenwinkelwerte entsprechend den Bereichen untersucht wird, die der verzögerten Synchronisation mit Signal 1 führend (ein Bereich um −90°) oder Signal 2 führend (ein Bereich um 90°), Signal 1, Signal 2 In-Phase-Synchronisation (ein Bereich um 0) entsprechen, und Signal 1, Signal 2 Anti-Phasen-Synchronisation (ein Bereich um +180° oder −180°).
   3. Definieren Sie den Parameter Schwellenwert. Geben Sie threshold = [threshold rsq val] ein. Der Standardwert ist Schwellenwert = 0.
      HINWEIS: Die Toolbox ermöglicht die Angabe eines Schwellenwertkohärenzwerts durch Angabe des Schwellenwertparameters. Dies ermöglicht es dem Forscher, Zeitpunkte mit einem bestimmten minimalen Kohärenzwert auszuwählen. Folglich werden nur Zeitpunkte berücksichtigt, deren Kohärenzwerte über dem angegebenen Schwellenwert liegen.
3. Laden Sie die Toolbox LeaderFollowerByPhase über den folgenden Link herunter (https://www.ariel.ac.il/wp/sns/download/ oder https://github.com/Minisharmaa/Leader-Follower-By-Phase).
4. Führen Sie die MATLAB-Funktion LeaderFollowerByPhase aus, indem Sie den Befehl cohervalues = LeaderFollowerByPhase(signal1, signal2, lowFreq, highFreq, phaseRange, threshold) in die Befehlszeile eingeben.
   HINWEIS: Die Kohärenz- und Phasenberechnungen werden mit den Funktionen WTC und XWT in MATLAB bzw.³⁰ durchgeführt.
5. Untersuchen Sie die Werte für die Synchronisierung in Phase, Signal 1, Signal 2 und Antiphase:
   1. Untersuchen Sie die Diagramme in MATLAB. Die Toolbox generiert eine Figur mit vier Plots.
      1. Kohärenz nach Art der Wechselwirkung: Untersuchen Sie das Boxchart-Diagramm oben links in der Abbildung, das das R-Quadrat (Rsq) für jede Art von Wechselwirkung (phasengleich, Signal 1 führend, Signal 2 führend, antiphasig) zeigt.
         HINWEIS: Eine detaillierte Beschreibung der integrierten Funktion des MATLAB-Boxcharts finden Sie unter folgendem Link (https://www.mathworks.com/help/matlab/ref/boxchart.html).
      2. Zentrale Indizes nach Art der Interaktion: Untersuchen Sie das Balkendiagramm oben rechts in der Ausgabeabbildung, in dem der maximale Mittelwert und Median für jede Art von Wechselwirkung (phasengleich, Signal 1 führend, Signal 2 führend, gegenphasig) angezeigt wird.
         HINWEIS: Eine detaillierte Beschreibung der integrierten Funktion der MATLAB-Leiste finden Sie unter folgendem Link (https://www.mathworks.com/help/matlab/ref/bar.html).
      3. Kohärenz im Zeitverlauf: Untersuchen Sie das Streudiagramm unten links in der Ausgabeabbildung, in dem die Kohärenzwerte und die Arten der Wechselwirkung im Zeitverlauf angezeigt werden. Die farbigen Punkte stehen für verschiedene Arten von Wechselwirkungen (schwarze Punkte stehen für die phasengleiche Synchronisation, dunkelgraue Punkte für Signal 1, hellgraue Punkte für Signal 2 und violette Punkte für die Antiphasensynchronisation).
         ANMERKUNG: Die Abbildung zeigt die Dynamik der Interaktion: den Austausch zwischen den vier Interaktionstypen während der gesamten Vollzeitreihe. Eine detaillierte Beschreibung der MATLAB-Streufunktion finden Sie unter folgendem Link (https://www.mathworks.com/help/matlab/ref/scatter.html).
      4. Zeitprozentsatz: Überprüfen Sie das Kreisdiagramm unten rechts in der Ausgabeabbildung, in dem die Zeiteinteilung nach den verschiedenen Interaktionstypen angezeigt wird.
         HINWEIS: Eine detaillierte Beschreibung der MATLAB-Kreisfunktion finden Sie unter folgendem Link (https://www.mathworks.com/help/matlab/ref/pie.html).
6. Überprüfen Sie die Ausgabetabelle mit den statistischen Werten (d. h. Mittelwert, Maximum, Median und Standardabweichung) für jede Art von Wechselwirkung (phasengleiche Synchronisation, Signal 1 führend, Signal 2 führend, Antiphasensynchronisation). In der Tabelle wird auch der Prozentsatz der Zeit angezeigt, in der die einzelnen Interaktionstypen aufgetreten sind. Jeder Interaktionstyp wird in einer anderen Spalte angezeigt.
7. Überprüfen Sie den Ausgabewert in der extrahierten Tabellenkalkulationsdatei (d. h. datatable.xlsx im aktuellen Ordner).

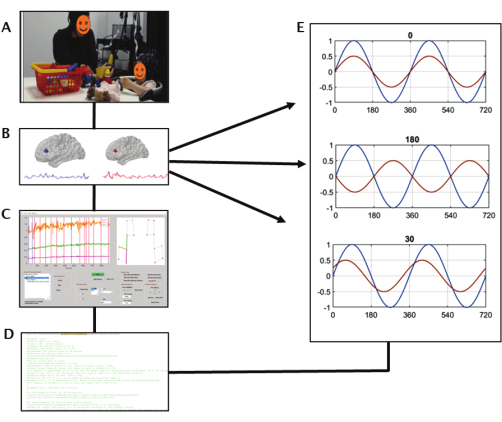
Abbildung 3: Überblick über den Arbeitsablauf. (A) Mutter-Kind-Dyaden, die sich im freien Spiel befanden, während fNIRS-Daten hyperscannten. (B) Illustration einer Mutter-Kind-Zeitreihe. (C) Vorverarbeitung der Zeitreihen mit Homer3. (D,E) Die Verwendung einer Toolbox zum Untersuchen verschiedener Arten von Interaktionen, z. B. phasengleiche Synchronisierung, Antiphasensynchronisierung und verzögerte Synchronisierung. Bitte klicken Sie hier, um eine größere Version dieser Abbildung anzuzeigen.

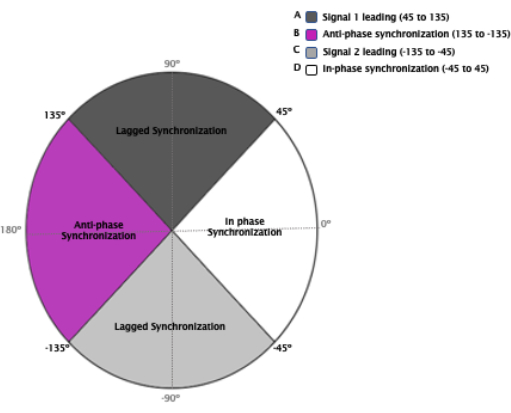
Abbildung 4: Klassifikation von vier verschiedenen Arten von Wechselwirkungen basierend auf der Phase. Dies stellt die Phasendifferenz der beiden neuronalen Zeitreihen in einem 360°-Modulo dar. Die Phasendifferenz kann man sich als Zeitverzögerung zwischen zwei Werten vorstellen und wird in Grad und Bogenmaß oder Bruchteilen der Wellenlänge gemessen. Hier wird das 360°-Modulo in vier verschiedene Bereiche unterteilt, die vier verschiedene Phasen der Wechselwirkung darstellen: (A) Signal 1 führend (ein Bereich um 90°, zwischen 45° und 135°), (B) Antiphasensynchronisation zwischen Signal 1 und Signal 2 (ein Bereich um 180° oder −180°, zwischen 135 und −135°), (C) Signal 2 führend (zwischen −135° und −45°), (D) In-Phase-Synchronisation (ein Bereich um 0, zwischen −45° und 45°). Diese Teilung ist der Standardansatz (45° um jeden Punkt); Die Toolbox erlaubt es jedoch, eine andere Abteilung zu konfigurieren. Während andere Konfigurationen möglicherweise nicht alle 360° abdecken, kann dies zu einer genaueren Definition der einzelnen Interaktionstypen führen. Bitte klicken Sie hier, um eine größere Version dieser Abbildung anzuzeigen.

Ergebnisse

In diesem Abschnitt werden die Arten von Analysen erläutert, die mit der Toolbox durchgeführt werden können (die unter https://www.ariel.ac.il/wp/sns/download/ oder https://github.com/Minisharmaa/Leader-Follower-By-Phase heruntergeladen werden kann. Für diese Analysen wurden fNIRS-Daten verwendet, die mit einer kleinen Stichprobe von Säuglings-Eltern-Dyaden gesammelt wurden. Sechs Paare von Mutter-Kind-Dyaden wurden mit einer validierten Verhaltensaufgabe, der Freispielaufgabe³¹, getestet, di...

Diskussion

Eine der gebräuchlichsten Methoden, die in fNIRS-Studien verwendet wird, ist die Wavelet-Transformationskohärenz (WTC), die ein Maß für die Kreuzkorrelation zweier Zeitreihen in Abhängigkeit von Frequenz und Zeit^{ist 10}. WTC berechnet die Kohärenz und Phasenverschiebung zwischen zwei Zeitreihen mit Hilfe von Korrelationsanalysen (Supplementary File 1). FNIRS-Hyperscanning-Studien haben WTC verwendet, um das Reizdarmsyndrom in vielen Funktionsbereichen zu schätzen, einschlie?...

Materialien

Name	Company	Catalog Number	Comments
NIRScout	NIRx Medical Technologies, LLC	n.a.	8 sources, 8 detectors
MATLAB	The Mathworks, Inc.	Matlab 2022a	In this protocol, several toolboxes and buit in MATLAB functions were used: HOMER3 toolbox was used to convert Intensity to OD, to remove motion artifacts through its function hmrMotionCorrectWavelet with default parameters and to convert OD to Conc. Wavelet Toolbox was used to compute WTC.