Se requiere una suscripción a JoVE para ver este contenido. Inicie sesión o comience su prueba gratuita.
Method Article
Descomposición de la varianza en comprensión de lectura para revelar los efectos únicos y común del lenguaje y decodificación
En este artículo
Resumen
Aquí presentamos un protocolo para la descomposición de la varianza en comprensión de lectura sobre los efectos del lenguaje y decodificación únicos y común.
Resumen
La Simple vista de la lectura es un modelo popular de la lectura que dice que la lectura es el producto de la descodificación y la lengua, con cada componente única predicción de comprensión de lectura. Aunque los investigadores han discutido si la suma más que el producto de los componentes es el mejor predictor, no investigadores han repartido la varianza explicada para examinar el grado en que los componentes comparten varianza en la predicción de lectura. Para descomponer la varianza, después restamos R2 para el modelo sólo lenguaje del modelo completo para obtener la única R2 para la descodificación. En segundo lugar, después restamos R2 para el modelo sólo descifrar el modelo completo para obtener la única R2 idiomas. En tercer lugar obtener la varianza común explicada por lenguaje y decodificación, restamos la suma de los dos único R2 R2 para el modelo completo. El método se demuestra en un enfoque de regresión con datos de los estudiantes en los grados 1 (n = 372), 6 (n = 309) y 10 (n = 122) utilizando una medida observada de la lengua (vocabulario receptivo), decodificación (lectura de la palabra tiempo) y lectora (test estandarizado). Los resultados revelan una cantidad relativamente grande de varianza en la lectura de comprensión en grado 1 por la variación común en la lengua y descifrar. Por el grado 10, sin embargo, es el único efecto del lenguaje y el efecto común del lenguaje y decodificación que explica la mayoría de la varianza en comprensión de lectura. Los resultados se discuten en el contexto de una versión ampliada de la Simple visión de lectura que considera efectos única y compartida de la lengua y descifrar en la predicción de comprensión de lectura.
Introducción
La Simple vista de la lectura1 (SVR) continúa como un modelo popular de lectura debido a su sencillez-lectura (R) es el producto de la decodificación (D) y lenguaje (L)- y porque SVR tiende a explicar, en promedio, aproximadamente el 60% de la varianza en la lectura comprensión2. SVR predice que las correlaciones entre D y R se reducirán con el tiempo y que las correlaciones entre L y R aumentará con el tiempo. Los estudios generalmente apoyan esta predicción3,4,5. Sin embargo, existen desacuerdos sobre la forma funcional de SVR, con modelos aditivos (D + L = R) explican más varianza en la lectura de comprensión que los modelos de producto (D × L = R)6,7,8y un combinación de suma y producto [R = D + L + (D × L) explicando la mayor cantidad de varianza en la lectura de comprensión3,9.
Recientemente el modelo SVR ha ampliado más allá de regresiones basados en variables observadas modelado variable latente mediante el análisis confirmatorio de la fábrica y modelado de ecuaciones estructurales. D generalmente se mide con tiempo o sin límite de tiempo lectura de palabras reales o nonwords y R se mide generalmente por una prueba de lectura estandarizada que incluye alfabetización y pasajes informativos seguidos por preguntas de opción múltiple. L por lo general se mide por pruebas de vocabulario expresivo y receptivo y, sobre todo en los grados de primaria, por medidas de sintaxis receptiva y expresiva y comprensión. Más estudios longitudinales reportan que L es unidimensional10,11,12,13. Sin embargo, otro estudio longitudinal14 informa de una estructura de dos factores para L en los grados de primaria y una estructura unidimensional en los grados 4 y 8. Estudios transversales recientes informan que un modelo bifactor mejor ajusta a los datos y predice R15,16,17,18. Por ejemplo, Foorman et al. 16 en comparación con modelos bifactor de SVR en datos de los estudiantes en grados 4-10, tres factores, cuatro factores y unidimensional y encontró que un modelo bifactor mejor y explicado 72 al 99% de la varianza de R. Un factor general de L explica varianza en todos los siete grados y vocabulario y sintaxis única explica varianza sólo en un grado. Aunque el factor D se correlacionó moderadamente con L y R en todos los grados (0.40-0.60 y 0.47 0.74, respectivamente), no fue únicamente correlacionado con R en presencia del factor general de L.
Aunque la modelo variable latente es SVR ampliado por arrojar luz sobre la dimensionalidad de la L y el único papel que juega la L en la predicción de R más allá de los grados de primaria, no hay estudios de SVR excepto uno por Foorman et al. 19 han repartido la varianza en la lectura de comprensión en lo que se debe únicamente a D y L y lo que se comparte en común. Esto es una gran omisión en la literatura. Expresiones es lógico que D y L comparten varianza en la predicción de lengua escrita porque conlleva de reconocimiento de palabra las habilidades lingüísticas de fonología, semántica y discurso en la oración y el texto nivel20. Del mismo modo, comprensión lingüística debe conectarse a representaciones ortográficas de fonemas, morfemas, palabras, oraciones y discurso, si el texto debe ser entendido21. Multiplicando D por L no cede el conocimiento compartido por estos componentes. Sólo la descomposición de la varianza en qué es y lo que es compartido por D y L en R predicción revelará el conocimiento integrado crucial para el éxito de las intervenciones educativas.
El único estudio por Foorman et al. 19 que descompone la varianza de la comprensión lectora qué es y qué es compartida en común por D y L emplea una variable latente enfoque de modelado. El siguiente protocolo demuestra la técnica con los datos de los estudiantes en los grados 1, 7 y 10 basado en solo observada variables de D (tiempo descifrar), L (vocabulario receptivo) y R (estandardizado prueba de comprensión de lectura) para hacer el proceso de descomposición fácil de entender. Los datos representan un subconjunto de los datos de Foorman et al. 19.
Protocolo
Nota: Los siguientes pasos describen descomposición total variación en una variable dependiente (Y) en componentes de varianza única varianza comúny varianza inexplicada basados en dos variables independientes seleccionadas (llamadas 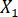 y
y 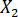 en este ejemplo) utilizando el software de gestión de datos y software con una interfaz gráfica de usuario (véase Tabla de materiales).
en este ejemplo) utilizando el software de gestión de datos y software con una interfaz gráfica de usuario (véase Tabla de materiales).
1. lectura de datos en el Software con una interfaz gráfica de usuario
- Haga clic en archivo.
- Coloca el ratón sobre abierto.
- Haga clic en datos.
- Busque el archivo de datos en el ordenador.
- Si el tipo de archivo no es compatible con el software con una interfaz gráfica de usuario, haga clic en Archivos de tipo y seleccione formato de archivo adecuado.
- Haga clic en abierto.
2. estimación de la varianza explicada en la Variable dependiente (Y)
-
Total varianza explicado basado en dos Variables independientes — Total R2.
Nota: Un valor de R2 es conocido como el coeficiente de determinación y representa la proporción de la varianza para una variable dependiente que es explicada por un conjunto de variables independientes.- Haga clic en analizar y coloca el ratón sobre regresión y seleccione Linear.
- Haga clic en la variable dependiente en la lista de variables. Haga clic en la flecha situada junto al dependiente.
- Haga clic en las dos variables independientes (X1 y X2) en la lista de variables. Haga clic en la flecha junto a Independent(s).
- Haga clic en Aceptar.
- Haga clic en la ventana del visor del software.
- Usa el ratón para desplazarse a la sección Resumen de modelo. Registre el valor en la columna R cuadrado y este valor Total R2la etiqueta.
-
Varianza total explicada basada en

- Repita los pasos 2.1.1 a 2.1.4 utilizando sólo
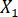 en la lista de variable independiente.
en la lista de variable independiente. - Haga clic en la ventana del visor del software.
- Usa el ratón para desplazarse a la sección Resumen de modelo. Registre el valor en la columna R cuadrado y este valor de la etiqueta
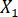 R2.
R2.
- Usa el ratón para desplazarse a la sección Resumen de modelo. Registre el valor en la columna R cuadrado y este valor de la etiqueta
- Repita los pasos 2.1.1 a 2.1.4 utilizando sólo
-
Varianza total explicada basada en
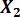
- Repita los pasos 2.1.1 a 2.1.4 utilizando sólo
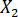 en la lista de variable independiente.
en la lista de variable independiente. - Haga clic en la ventana del visor del software.
- Usa el ratón para desplazarse a la sección Resumen de modelo. Registre el valor en la columna R cuadrado y este valor de la etiqueta
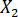 R2.
R2.
- Usa el ratón para desplazarse a la sección Resumen de modelo. Registre el valor en la columna R cuadrado y este valor de la etiqueta
- Repita los pasos 2.1.1 a 2.1.4 utilizando sólo
3. cálculo de los componentes de varianza única, común e inexplicable
- Abra el software de gestión de datos.
- Introduzca las etiquetas Total R2,
 R2, y
R2, y 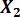 R2 en las células A1, B1 y C1, respectivamente.
R2 en las células A1, B1 y C1, respectivamente. - Introduzca el valor de2 Total Rdesde el paso 2.1.5.1 en la celda A2.
- Entrar en la
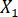 R2 valor del paso 2.2.2.1 en celda B2.
R2 valor del paso 2.2.2.1 en celda B2. - Entrar en la
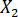 R2 valor del paso 2.3.2.1 en la celda C2.
R2 valor del paso 2.3.2.1 en la celda C2. - Calcular la varianza única de 1 Variable (U
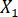 R2) en el software de gestión de datos.
R2) en el software de gestión de datos.- En la celda D2 tipo: "= A2-C2" (es decir, Total R2 menos
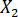 R2). En la celda D1 de la etiqueta este valor U
R2). En la celda D1 de la etiqueta este valor U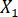 R2.
R2.
- En la celda D2 tipo: "= A2-C2" (es decir, Total R2 menos
- Calcular la varianza única de 2 variables (U
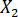 R2) en el software de gestión de datos.
R2) en el software de gestión de datos.- En la celda E2 tipo: "= A2-B2" (es decir, Total R2 menos
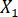 R2). En la celda E1 la etiqueta este valor U
R2). En la celda E1 la etiqueta este valor U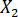 R2.
R2.
- En la celda E2 tipo: "= A2-B2" (es decir, Total R2 menos
- Calcular la varianza común entre las Variables 1 y 2 (C
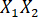 R2) en el software de gestión de datos.
R2) en el software de gestión de datos.- En la celda F2 tipo: "= A2-D2-E2" (es decir, Total R2 menos U
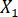 R2 menos U
R2 menos U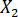 R2). En la celda F1 etiqueta este valor C
R2). En la celda F1 etiqueta este valor C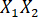 R2.
R2.
- En la celda F2 tipo: "= A2-D2-E2" (es decir, Total R2 menos U
- Calcular la varianza inexplicada (e) en el software de gestión de datos.
- En la celda G2 tipo: «= 1-A2» (es decir, Total 1 R2). En la celda G1 etiqueta este valor e.
4. trazar la UX1R2, UX2R2, CX1X2R2y e valores
Nota: Los valores de las celdas D2, E2, F2 y G2 se trazan.
- Haga clic y arrastre el ratón sobre celdas D2, E2, F2 y G2 para resaltar los datos.
- Haga clic en Insertar en la cinta de opciones del software de administración de datos.
- Haga clic en cartas | Gráfico | gráfico 2-D.
Resultados
El objetivo de este estudio fue investigar las contribuciones de varianza única y común de lenguaje (L) y (D) el descifrar de predicción lectora (R) en los grados 1, 7 y 10 en Florida, un Estado cuya Demografía son representativas de la nación como un conjunto. Había dos hipótesis con respecto a las predicciones de la varianza explicada en la comprensión lectora. En primer lugar, después de los grados de primaria, disminuirá significativamente la contribución única de D, y aum...
Discusión
Hay tres pasos importantes en el protocolo para la descomposición de la varianza de R en una única y común varianza debido a L y D. En primer lugar, restar R2 en el modelo sólo L del modelo completo para obtener la única R2 d. En segundo lugar, restar R2 para el modelo D-sólo el modelo completo para obtener la única R2 para tercero de L., para obtener la varianza común explicada por L y D, reste la suma de los dos único R2 R2 para el modelo comple...
Divulgaciones
Los autores declaran que no tienen intereses financieros que compiten.
Agradecimientos
La investigación divulgada aquí fue apoyada por el Instituto de Ciencias de la educación, Departamento de educación, a través de una subaward a la Universidad Estatal de Florida de Grant R305F100005 al servicio de prueba educativo como parte de la lectura para la comprensión Iniciativa. Las opiniones expresadas son las de los autores y no representan opiniones del Instituto, el Departamento de Educación de Estados Unidos, el Educational Testing Service o Universidad Estatal de Florida.
Materiales
| Name | Company | Catalog Number | Comments |
| IBM SPSS Statistics Software | IBM | ||
| Microsoft Office Excel | Microsoft |
Referencias
- Gough, P., Tunmer, W. Decoding, reading, and reading disability. Remedial and Special Education. 7, 6-10 (1986).
- Quinn, J. M., Wagner, R. K. Using meta-analytic structural equation modeling to study developmental change in relations between language and literacy. Child Development. , (2018).
- Chen, R. S., Vellutino, F. Prediction of reading ability: A cross-validation study of the simple view of reading. Journal of Literacy Research. 29 (1), 1-24 (1997).
- Catts, H., Hogan, T., Adlof, S., Catts, H., Kamhi, A. Developmental changes in reading and reading disabilities. Connections between language and reading disabilities. , (2005).
- Gough, P., Hoover, W., Peterson, C., Cornoldi, C., Oakhill, J. Some observations on the simple view of reading. Reading comprehension difficulties. , (1996).
- Dreyer, L., Katz, L. An examination of "The Simple View of Reading.". Haskins Laboratories Status Report on Speech Research. SR-111/112. , 161-166 (1992).
- Neuhaus, G., Roldan, L., Boulware-Gooden, R., Swank, P. Parsimonious reading models: Identifying teachable subskills. Reading Psychology. 27, 37-58 (2006).
- Kershaw, S., Schatschneider, C. A latent variable approach to the simple view of reading. Reading and Writing. 25, 433-464 (2012).
- Hoover, W., Gough, P. The simple view of reading. Reading and Writing. 2, 127-160 (1990).
- Adlof, S., Catts, H., Little, T. Should the simple view of reading include a fluency component?. Reading & Writing. 19, 933-958 (2006).
- Anthony, J., Davis, C., Williams, J., Anthony, T. Preschoolers' oral language abilities: A multilevel examination of dimensionality. Learning and Individual Differences. 35, 56-61 (2014).
- Bornstein, M., Hahn, C., Putnick, D., Suwalsky, J. Stability of core language skill from early childhood to adolescence: A latent variable approach. Child Development. 85, 1346-1356 (2014).
- Protopapas, A., Simos, P., Sideridis, G., Mouzaki, A. The components of the simple view of reading: A confirmatory factor analysis. Reading Psychology. 33, 217-240 (2012).
- Tomblin, J. B., Zhang, X. The dimensionality of language ability in school-age children. Journal of Speech, Language, and Hearing Research. 49, 1193-1208 (2006).
- Foorman, B., Herrera, S., Petscher, Y., Mitchell, A., Truckenmiller, A. The Structure of Oral Language and Reading and Their Relation to Comprehension in grades kindergarten through grade 2. Reading and Writing. 28 (5), 655-681 (2015).
- Foorman, B., Koon, S., Petscher, Y., Mitchell, A., Truckenmiller, A. Examining General and Specific Factors in the Dimensionality of Oral Language and Reading in 4th-10th Grades. Journal of Educational Psychology. 107 (3), 884-899 (2015).
- Kieffer, M., Petscher, Y., Proctor, C. P., Silverman, R. Is the whole greater than the sum of its parts? Modeling the contributions of language comprehension skills to reading comprehension in the upper elementary grades. Scientific Studies of Reading. 20 (6), 436-454 (2016).
- Kim, Y. S. G., Park, C., Park, Y. Dimensions of discourse level oral language skills and their relation to reading comprehension and written composition: an exploratory study. Reading and Writing. 28, 633-654 (2015).
- Foorman, B., Petscher, Y., Herrera, S. Unique and common effects of decoding and language factors in predicting reading comprehension in grades 1-10. Learning and Individual Differences. 63, 12-23 (2018).
- Perfetti, C. Reading ability: Lexical quality to comprehension. Scientific Studies of Reading. 11 (4), 357-383 (2007).
- Perfetti, C., Stafura, J. Word knowledge in a theory of reading comprehension. Scientific Studies of Reading. 18 (4), 22-37 (2014).
- Torgesen, J., Wagner, R., Rashotte, C. . Test of Word Reading Efficiency. , (2012).
- Dunn, L., Dunn, D. . Peabody Picture Vocabulary Test-4. , (2007).
- MacGinitie, W., MacGinitie, R., Maria, K., Dreyer, L. . Gates-MacGinitie Reading Tests. , (2000).
- Wanzek, J., Wexler, J., Vaughn, S., Ciullo, S. Reading interventions for struggling readers in the upper elementary grades: a synthesis of 20 years of research. Reading & Writing. 23, 889-912 (2010).
- Foorman, B., Petscher, Y., Stanley, C., Herrera, S. Latent profiles of reading and language and their association with standardized reading outcomes in kindergarten through tenth grade. Journal of Research on Educational Effectiveness. 10 (3), 619-645 (2017).
- Lesaux, N. K., Kieffer, M. J., Kelley, J. G., Harris, J. Effects of academic vocabulary instruction for linguistically diverse adolescents: Evidence from a randomized field trial. American Educational Research Journal. 51 (6), 1159-1194 (2014).
- Lawrence, J., Crosson, A., Paré-Blagoev, E., Snow, C. Word generation randomized trial: Discussion mediates the impact of program treatment on academic word learning. American Educational Research Journal. 52 (4), 750-786 (2015).
Reimpresiones y Permisos
Solicitar permiso para reutilizar el texto o las figuras de este JoVE artículos
Solicitar permisoThis article has been published
Video Coming Soon
ACERCA DE JoVE
Copyright © 2025 MyJoVE Corporation. Todos los derechos reservados